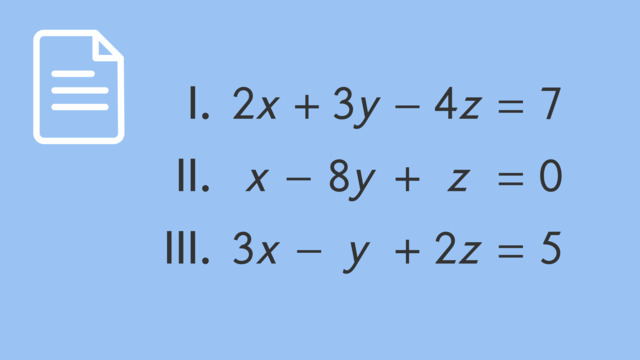Lineare Gleichungssysteme
Lineare Gleichungssysteme enthalten mehrere Gleichungen, die du gleichzeitig lösen musst. Lerne die wichtigsten Methoden wie das Gauß-Verfahren und finde heraus, wie du komplexe Systeme mit Leichtigkeit bewältigst. Neugierig? Erfahre mehr über die vielseitigen Lösungsansätze!
in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Lerntext zum Thema Lineare Gleichungssysteme
Lineare Gleichungssysteme – Einführung
Was ist eigentlich ein lineares Gleichungssystem? Ein lineares Gleichungssystem besteht aus mindestens zwei Gleichungen mit mehreren Unbekannten, die gleichzeitig erfüllt sein müssen. Ziel ist es im Normalfall, eine gemeinsame Lösung zu finden, die alle Gleichungen gleichzeitig erfüllt.
Ein lineares Gleichungssystem (LGS) enthält mehrere lineare Gleichungen, also Gleichungen, in denen die Variablen nicht potenziert oder miteinander multipliziert werden. Die allgemeine Form für zwei Gleichungen mit zwei Unbekannten lautet:
$$ \begin{array}{ccc} a_{1}x + b_{1}y &=& c_{1}\\[5pt] a_{2}x + b_{2}y &=& c_{2} \end{array} $$
Dabei sind $a_{1}, b_{1}, c_{1}, a_{2}, b_{2}, c_{2}$ bekannte Zahlen und $x$ sowie $y$ die Unbekannten.
Lineare Gleichungssysteme lösen – Beispiele
Lineare Gleichungssysteme kannst du mit unterschiedlichen Lösungsverfahren lösen:
Zur Wiederholung kannst du dir die klassischen drei Lösungsverfahren noch einmal genauer anschauen. Wir betrachten dabei einfachheitshalber LGS mit zwei Gleichungen und zwei Unbekannten, die Prinzipien lassen sich aber genauso auf LGS mit mehr Gleichungen und Unbekannten übertragen. Für größere LGS bietet sich vor allem der Gauß-Algorithmus an.
Gauß-Verfahren
Für LGS, die aus drei oder mehr Gleichungen bestehen, ist das Gauß-Verfahren häufig ein guter Ansatz, da es immer zum Ziel führt, ohne dass man den Überblick verliert. Mithilfe des Additionsverfahrens wird dabei das LGS zunächst in die sogenannte Stufenform gebracht, in der die Lösung für eine Variable in der untersten Gleichung einfach abzulesen ist. Dann können mit der bestimmten Variable und dem Einsetzungsverfahren Schritt für Schritt auch die restlichen Variablen bestimmt werden.
Ausblick – das lernst du nach lineare Gleichungssysteme
Nachdem du nun die grundlegenden Verfahren zur Lösung linearer Gleichungssysteme kennst, kannst du dich weiter mit komplexeren Methoden wie dem Einsatz von Matrizen in der linearen Algebra beschäftigen. Zum Lösen von LGS kannst du dann auch die Determinante im Zusammenhang mit der cramerschen Regel anwenden.
Zusammenfassung zum Thema Lineare Gleichungssysteme
- Ein lineares Gleichungssystem besteht aus mehreren linearen Gleichungen, die gleichzeitig erfüllt sein müssen.
- Es gibt verschiedene Lösungsverfahren wie das Gleichsetzungs-, Einsetzungs- und Additionsverfahren.
- Das wichtigste Verfahren zur Lösung von LGS in der Oberstufe ist das Gauß-Verfahren.
Häufig gestellte Fragen zum Thema Lineare Gleichungssysteme
9.966
sofaheld-Level
6.600
vorgefertigte
Vokabeln
7.801
Lernvideos
37.167
Übungen
32.630
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Schulstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung


 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?