Lineare Gleichungssysteme – Beispielaufgaben
Mit Hilfe linearer Gleichungssysteme kann man oftmals wichtige Zusammenhänge beschreiben, welche man dann mit dem Einsetzungs-, Gleichsetzungs- oder Additionsverfahren lösen kann.
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Lineares Gleichungssystem
- Anwendungsbeispiel: Additionsverfahren
- Anwendungsbeispiel: Gleichsetzungsverfahren
- Anwendungsbeispiel: Einsetzungsverfahren
Lineares Gleichungssystem
Ein lineares Gleichungssystem (LGS) besteht aus mehreren linearen Gleichungen und ist eindeutig lösbar, wenn es über mindestens so viele Gleichungen wie Variablen verfügt.
In den nachfolgenden Aufgaben wird gezeigt, in welchen Zusammenhängen LGS beim Lösen eines Problems hilfreich sein können. Zum Lösen von LGS werden drei verschiedene Verfahren vorgestellt.
Anwendungsbeispiel: Additionsverfahren
Auf einem Bauernhof gibt es ein Gehege, in dem sich Schweine und Hühner befinden. Emilia zählt insgesamt $50$ Köpfe und $116$ Beine. Wie viele Hühner und Schweine sind es?

Um diese Aufgabe mit einem LGS zu lösen, legt man die Variablen fest und stellt Gleichungen auf:
- $x$: Anzahl der Schweine (pro Schwein gilt ein Kopf und vier Beine)
- $y$: Anzahl der Hühner (pro Huhn gilt ein Kopf und zwei Beine)
Aus dem Aufgabentext erschließen sich zwei Informationen:
- Wenn es $50$ Köpfe gibt, dann befinden sich $50$ Tiere im Gehege.
- Zählt man die Beine der Schweine und Hühner zusammen, so ergeben sich $116$ Beine.
Demnach kann das folgende LGS aufgestellt werden:
$\begin{array}{llll} \text{I} && x +y &=& 50 \\ \text{II} && 4x + 2y &=& 116 \end{array}$
Um das LGS zu lösen, wird in diesem Fall das Additionsverfahren verwendet. Durch Umformen der ersten Gleichung erhält man:
$\begin{array}{llllll} \text{I} && x + y &=& 50 & \vert \cdot (-2) \\ \\ \text{I'} && -2x -2y &=& -100 & \\ \text{II} && 4x + 2y &=& 116 & \end{array}$
Nach Addition der Gleichungen ($\text{I'}$) und ($\text{II}$) fällt die Variable $y$ heraus:
$\begin{array}{llll} \left(\text{I'}+\text{II}\right): && 2x &=& 16 & \vert : 2 \end{array}$
Es ergibt sich eine Gleichung mit einer Variablen, nach der aufgelöst wird: $x = 8$
Die zweite Variable $y$ bestimmt man durch Einsetzen des $x$-Wertes in eine der beiden Ausgangsgleichungen. In diesem Fall bietet sich die erste einfachere Gleichung an:
$\begin{array}{llll} 8 + y &=& 50 & \vert - 8 \\ y &=& 42 \end{array}$
Die Lösungsmenge dieses Gleichungssystems lautet $\mathbb{L} = \lbrace(8\vert 42)\rbrace$, also handelt es sich um $8$ Schweine und $42$ Hühner.
Anwendungsbeispiel: Gleichsetzungsverfahren
Ein Elektrizitätswerk bietet folgende Tarife an:
- Tarif A: monatlicher Grundpreis $150$ €, Arbeitspreis $20$ Cent pro $\text{kWh}$.
- Tarif B: monatlicher Grundpreis $180$ €, Arbeitspreis $15$ Cent pro $\text{kWh}$.

Wie viele Kilowattstunden müssen abgenommen werden, damit es sich lohnt, Tarif B zu wählen? Wie hoch ist dann die Rechnung vom Elektrizitätswerk?
Wie schon in der ersten Aufgabe werden auch hier zunächst zwei Variablen festgelegt:
- $x$: Kilowattstunden
- $y$: Preis in €
Es lassen sich zwei Gleichungen aufstellen für Tarif A und Tarif B:
$\begin{array}{lllll} \text{I} && y &=& 150 + 0,2x \\ \text{II} && y &=& 180 + 0,15x \end{array}$
Da in beiden Gleichungen die Variable $y$ alleine auf der linken Seite steht, bietet sich das Gleichsetzungsverfahren an, d.h. die rechten Seiten werden gleichgesetzt und man erhält eine Gleichung mit der Variablen $x$, nach der aufgelöst wird:
$\begin{array}{llll} 150 + 0,2x &=& 180 + 0,15x & \vert - 150 \\ 0,2x &=& 30 + 0,15x & \vert - 0,15x \\ 0,05x &=& 30 & \vert :0,05 \\ x &=& 600 & \end{array}$
Um nun den $y$-Wert zu ermitteln, wird der errechnete $x$-Wert in eine der beiden Ausgangsgleichungen eingesetzt:
$\begin{array}{lll} y &=& 150 + 0,2\cdot 600 \\ y & = & 270 \end{array}$
Die errechnete Lösungsmenge $\mathbb{L} = \lbrace (600\vert 270)\rbrace $ lässt sich so interpretieren: Bei einer Abnahme von $600$ Kilowattstunden sind die beiden Tarife A und B gleich, nämlich $270 €$. Bei einer Abnahme von mehr als $600$ Kilowattstunden würde sich dann Tarif B lohnen.
Anwendungsbeispiel: Einsetzungsverfahren
Nicht nur in Textaufgaben, sondern auch geometrisch gesehen, ist die Verwendung eines LGS sinnvoll:
Der Schnittpunkt zweier Geraden im Koordinatensystem soll rechnerisch bestimmt werden. Die Geradengleichungen lauten:
$\begin{array}{lllll} g_1: && 2x &=& 2y - 2 \\ g_2: && y &=& -2x + 4 \end{array}$
Auch hier gibt es zwei Gleichungen mit zwei Variablen, die sich als LGS auffassen lassen, da ihre Lösungsmenge der gemeinsame Schnittpunkt $S(x \vert y)$ ist:
$\begin{array}{lllll} \text{I} && 2x &=& 2y - 2 \\ \text{II} && y &=& -2x + 4 \end{array}$
In diesem LGS steht $y$ in der zweiten Gleichung isoliert. Für $y$ kann die rechte Gleichungsseite in die erste Gleichung eingesetzt werden, also ($\text{I}$) in (\text{II}), damit man eine Gleichung mit einer Variablen erhält. Dieses Verfahren heißt Einsetzungsverfahren:
$\begin{array}{llll} 2x &=& 2\cdot (-2x + 4) - 2 & \\ 2x &=&-4x + 8 - 2 & \\ 2x &=& -4x + 6 & +4x \\ 6x &=& 6 & :6 \\ x &=& 1 \end{array}$
$y$ bestimmt man durch Einsetzen des $x$-Wertes in eine der Geradengleichungen:
$\begin{array}{lll} y &=& -2\cdot 1 + 4 \\ y &=& 2 \end{array}$
Die Lösungsmenge $\mathbb{L} = \lbrace (1\vert 2)\rbrace $ stellt die Koordinaten des Schnittpunktes dar, also $S (1 \vert 2)$.
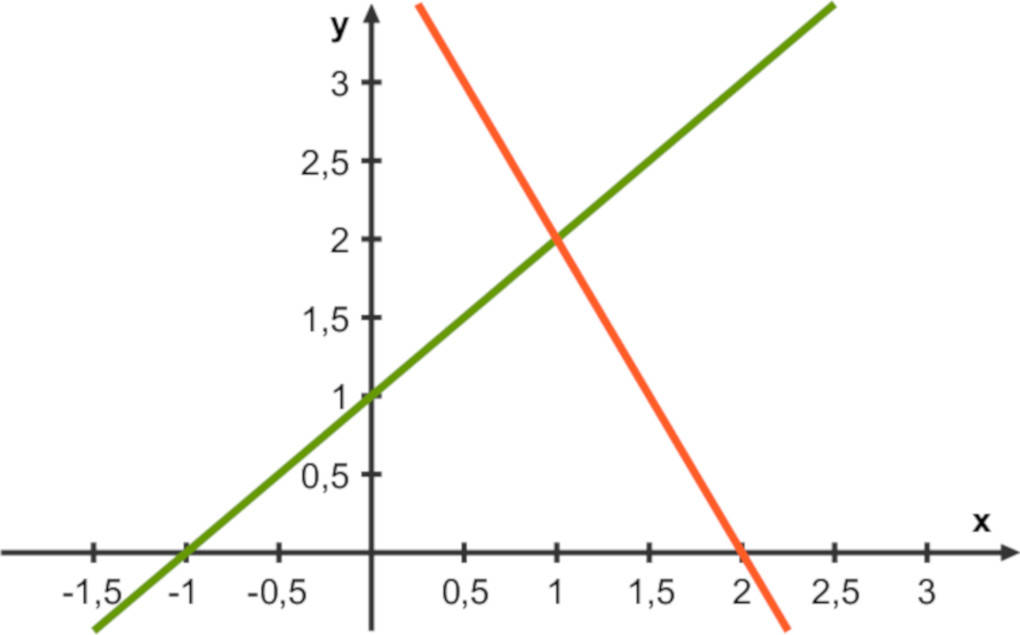
Graphisch lässt sich der Schnittpunkt der Geraden darstellen, wenn man die erste Geradengleichung auf die Normalform $y = m\cdot x + b$ bringt und die Graphen dann ins Koordinatensystem zeichnet:
$\begin{array}{lll} g_1: && y = x + 1\\ g_2: && y = -2x + 4 \end{array}$
Alle Videos und Lerntexte zum Thema
Videos und Lerntexte zum Thema
Lineare Gleichungssysteme – Beispielaufgaben (4 Videos, 1 Lerntext)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Lineare Gleichungssysteme – Beispielaufgaben (4 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung





 Lineare Gleichungssysteme mit zwei Variablen – Definition
Lineare Gleichungssysteme mit zwei Variablen – Definition
 Additionsverfahren
Additionsverfahren
 Einsetzungsverfahren
Einsetzungsverfahren
 Gleichsetzungsverfahren
Gleichsetzungsverfahren









