Was ist ein Vektor?
Ein Vektor ist ein mathematisches Objekt mit Richtung, Orientierung und Länge, zum Beispiel zur Beschreibung von Bewegungen. Ein Vektor wird als Pfeil im Koordinatensystem dargestellt. Interessiert? Dies und mehr erfährst du im vollständigen Text.


in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.

Grundlagen zum Thema Was ist ein Vektor?
Vektor – Definition
Hast du das Wort Vektor schon einmal gehört? Es kommt ursprünglich aus dem Lateinischen und bedeutet so viel wie Träger oder Fahrer.
Ein Vektor ist ein mathematisches Objekt, das durch einen Pfeil dargestellt werden kann.
Ein Vektor hat einen Anfangspunkt und einen Endpunkt (die Pfeilspitze) und ist in der Regel dazu da, eine Richtung auszudrücken.
Jeder Vektor kann durch einen Vektorpfeil im Koordinatensystem dargestellt werden. In der Physik und Mathematik nutzt man Vektoren und die Vektorrechnung vor allem, um gerichtete Vorgänge zu beschreiben – also Vorgänge, die in eine bestimmte Richtung ablaufen, zum Beispiel die Verschiebung eines Objekts.
Vektorielle Größen werden auch als gerichtete Größen bezeichnet. Physikalische Kräfte wie die Gewichtskraft sind beispielsweise gerichtete Größen – sie werden durch einen Kraftpfeil dargestellt. Auch Bewegungsrichtungen von Körpern wie einem Auto oder einem Flugzeug können mit Vektoren bzw. Vektorpfeilen dargestellt werden.
Im Folgenden betrachten wir ein Beispiel, um die Grundlagen von Vektoren besser zu verstehen.
Vektoren – Beispiel
Wir betrachten zwei Flugzeuge, die in entgegengesetzte Richtungen fliegen. Flugzeug $A$ fliegt mit einer Geschwindigkeit von $200~\frac{\text{km}}{\text{h}}$ von links nach rechts. Flugzeug $B$ fliegt mit einer Geschwindigkeit von $400~\frac{\text{km}}{\text{h}}$ von rechts nach links. Wir können Vektoren benutzen, um die Bewegungsrichtungen und auch die Geschwindigkeiten der Flugzeuge darzustellen.
Vektoren werden in der Schulmathematik als Pfeile dargestellt. Weil wir in diesem Beispiel die Geschwindigkeiten darstellen wollen, zeigen die Pfeile in Richtung der Bewegungen. Für das Flugzeug $A$ haben wir deswegen einen Pfeil gezeichnet, der nach rechts zeigt. Für Flugzeug $B$ zeigt der Pfeil nach links.
Die beiden Pfeile verlaufen genau parallel zueinander, aber mit unterschiedlicher Orientierung. Die Orientierung wird durch die Ausrichtung der Pfeilspitze festgelegt, während die Richtung durch die Lage der Linie im Raum bestimmt wird.
Der Pfeil für Flugzeug $B$ ist außerdem doppelt so lang wie der Pfeil von Flugzeug $A$. Darin spiegelt sich die doppelte Geschwindigkeit wider: Die Länge des Vektors entspricht der Höhe der Geschwindigkeit. Man nennt die Länge auch den Betrag des Vektors. Diese ersten Erkenntnisse können wir schon zusammenfassen:
Vektor – Eigenschaften
- Ein Vektor wird in der analytischen Geometrie als (Vektor-)Pfeil dargestellt.
- Ein Vektor hat eine feste Länge, Richtung und Orientierung und ist durch diese drei Eigenschaften vollständig bestimmt.
- Zwei Vektoren sind genau dann gleich, wenn sie die gleiche Länge, die gleiche Richtung und die gleiche Orientierung haben.
- Ein Vektor eignet sich zur Beschreibung einer Verschiebung.
Kennst du das?
Vielleicht hast du schon einmal auf einer Wanderung bemerkt, wie der Wind dich in eine bestimmte Richtung drückt. Dieser Wind hat eine Richtung und eine Stärke – genau wie ein Vektor in der Mathematik. Ein Vektor beschreibt eine Größe mit einer Richtung und einem Betrag, genauso wie der Wind, der dich nach vorne oder zur Seite schiebt. So kannst du dir Vektoren besser vorstellen: sie sind wie unsichtbare Kräfte, die Dinge bewegen.
Vektoren – Koordinatenschreibweise
Vektoren werden in der Mathematik durch Kleinbuchstaben mit einem kleinen Pfeil darüber bezeichnet, zum Beispiel so:
$\vec{a}$, $\vec{b}$, $\vec{c}$
In einem zweidimensionalen Raum hat jeder Vektor zwei Komponenten, die in der Regel mit $x$ und $y$ bezeichnet werden. Diese Komponenten können in Form von Koordinaten in Klammern geschrieben werden, also so:
$\vec{a} = \left(x, y \right)$
Aber auch die Schreibweise als sogenannter Spaltenvektor wird oft verwendet:
$\vec{a} = \begin{pmatrix} x \\ y \end{pmatrix}$
In einem dreidimensionalen Raum wird entsprechend noch eine dritte Komponente (meist $z$) ergänzt:
$\vec{a} = \begin{pmatrix} x \\ y \\ z \end{pmatrix}$
Manchmal werden statt $x$, $y$ und $z$ auch die Bezeichnungen $x_1$, $x_2$ und $x_3$ für die Komponenten verwendet:
$\vec{a} = \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix}$
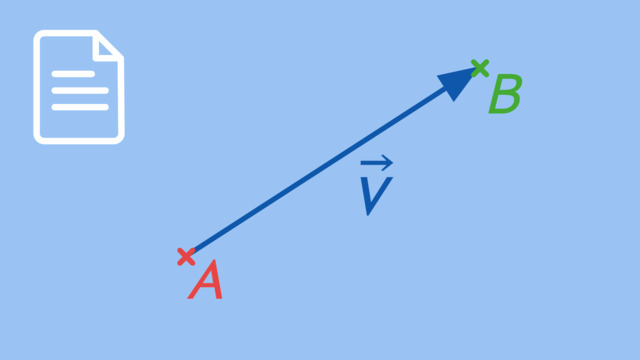
Alternativ zur Schreibweise $\vec{a}$ kann man auch den Anfangs- und Endpunkt des Vektors mit einem Pfeil überschreiben. Bei einem Anfangspunkt $A$ und einem Endpunkt $B$ sähe das zum Beispiel so aus:
$\vec{a} = \overrightarrow{AB}$
Der Nullvektor
Ein besonderer Vektor ist der Nullvektor. Sein Betrag bzw. seine Länge ist null. Er ist damit, entsprechend der Zahl Null, das neutrale Element der Vektoraddition. Das bedeutet, wenn man einen Vektor $\vec{a}$ um den Nullvektor verlängert, bleibt der Vektor gleich:
$\vec{a} + \vec{0} = \vec{a}$
Fehleralarm
Viele Schülerinnen und Schüler verwechseln den Nullvektor mit der Null. Der Nullvektor ist zwar ein Vektor, hat aber keine Richtung, während die Null ein Skalar ist.
Der Ortsvektor
Einen Vektor, dessen Anfangspunkt im Ursprung des Koordinatensystems liegt, nennt man Ortsvektor. Er gibt die Position dieses Punktes relativ zum Ursprung an. Jeder Punkt im Raum hat genau einen zugehörigen Ortsvektor, dessen Vektoreinträge den Koordinaten des Punktes entsprechen. Der Ortsvektor mit dem Endpunkt $A$ kann demnach auch als Vektor $\overrightarrow{OA}$ bezeichnet werden.
Der Gegenvektor
Hat ein Vektor die gleiche Länge und Orientierung wie ein anderer, aber eine gegensätzliche Richtung, bezeichnet man diese Vektoren als Gegenvektoren. Anschaulich bedeutet das, dass der Ausgangsvektor um $180$ Grad gedreht werden muss, um den Gegenvektor zu erhalten. Man kann dies auch durch ein negatives Vorzeichen anzeigen. Das Vorzeichen aller Vektoreinträge dreht sich dadurch um. Wenn beispielsweise die Vektoren $\vec{a}$ und $\vec{b}$ Gegenvektoren sind, gilt:
$\vec{a} = - \vec{b}$
Wusstest du schon?
Vektoren sind nicht nur in der Mathematik wichtig, sondern auch in der Videospielwelt! Viele 3D-Spiele nutzen Vektoren, um Bewegungen und Positionen von Figuren und Objekten zu berechnen. Also, das nächste Mal, wenn du ein Spiel spielst, denk dran: Vektoren sorgen dafür, dass alles im Spiel flüssig und realistisch aussieht!
Betrag eines Vektors
Wenn man anzeigen möchte, dass der Betrag eines Vektors gemeint ist, setzt man den Vektor in Betragsstriche, also zwei vertikale Striche. Der Betrag eines Vektors ist damit (wie der Betrag einer Zahl) immer größer oder gleich null.
$\vert \vec{a} \vert = \big \vert \overrightarrow{AB} \big \vert \geq 0$
Mit dem Betrag eines Vektors kann seine Länge berechnet werden.
Vektoren – Übung
Sehen wir uns ein paar weitere Beispiele an, um die Bezeichnungen zu üben:
Die Vektoren $\vec{a}$ und $\vec{c}$ haben die gleiche Richtung, Orientierung und Länge. Wir können deshalb schreiben:
$\overrightarrow{AB} = \vec{a} = \vec{c} = \overrightarrow{CD} ~ ~ ~ \text{und} ~ ~ ~ \vert \vec{a} \vert = \vert \vec{c} \vert$
Die Vektoren $\vec{c}$ und $\vec{e}$ sind zwar parallel, haben also grundsätzlich die gleiche Richtung, allerdings entgegengesetzte Orientierung. Da sie auch die gleiche Länge (also den gleichen Betrag) haben, handelt es sich um Gegenvektoren. Wir können also schreiben:
$\vec{c} = - \vec{e}$
Schlaue Idee
Wenn du beim Billard spielst, kannst du dir die Kugeln als Vektoren vorstellen. Der Vektor gibt dir die Richtung und Stärke des Stoßes an, die du brauchst, um eine Kugel in ein Loch zu befördern.
Die Vektoren $\vec{e}$ und $\vec{g}$ haben zwar den gleichen Betrag, aber unterscheiden sich in Richtung und Orientierung. Sie sind weder gleich noch Gegenvektoren zueinander:
$\vert \vec{e} \vert = \vert \vec{g} \vert ~ ~ ~ \text{aber} ~ ~ ~ \vec{e} \neq \vec{g} ~ ~ ~ \text{und} ~ ~ ~ \vec{e} \neq -\vec{g}$
Die Vektoren $\vec{g}$ und $\vec{i}$ stimmen zwar hinsichtlich ihrer Richtung und Orientierung überein, haben aber unterschiedlich große Beträge: Der Vektor $\vec{i}$ ist doppelt so lang wie der Vektor $\vec{g}$:
$\vert \vec{i} \vert = 2 \cdot \vert \vec{g} \vert ~ ~ ~ \text{aber} ~ ~ ~ \vec{g} \neq \vec{i} ~ ~ ~ \text{und} ~ ~ ~ \vec{g} \neq -\vec{i}$
Vektoren – Anwendungsbeispiel
Mithilfe von Vektoren können geometrische Objekte beschrieben und konstruiert werden, zum Beispiel Prismen. Sieh dir dieses Prisma an:
Alle Kanten des Prismas können durch Vektoren dargestellt werden. Die dreieckige Grundfläche des Prismas wird durch die Vektoren $\vec{a}$, $\vec{c}$ und $\vec{d}$ aufgespannt. Diese drei Vektoren spannen ebenso die gegenüberliegende Seite auf.
Wir können für die beiden dreieckigen Seiten des Prismas die gleichen Bezeichnungen für die entsprechenden Vektoren verwenden, denn die Vektoren der Kanten sind zwar räumlich zueinander verschoben, haben aber immer noch die gleiche Richtung, Orientierung und Länge. In der Abbildung gleichfarbig dargestellte Vektoren sind also gleich. Man spricht in diesem Zusammenhang davon, dass ein Vektor nicht ortsgebunden ist.
Die verbleibende Kantenlänge wird durch den Vektor $\vec{b}$ dargestellt, der ebenfalls nicht ortsgebunden ist und so die drei übrigen Kanten des Prismas beschreibt.
Die Abbildung verdeutlicht auch, wie Vektoren verwendet werden, um eine Verschiebung im Raum auszudrücken. Die obere Seite des Prismas, die durch die Vektoren $\vec{a}$, $\vec{c}$ und $\vec{d}$ aufgespannt wird, wird entlang des Vektors $\vec{b}$ verschoben und stellt so auch die dreieckige Grundfläche dar. Diese Verschiebung ist durch die Richtung, Orientierung und Länge von $\vec{b}$ eindeutig festgelegt.
Ausblick – das lernst du nach Was ist ein Vektor?
Als Nächstes kannst du dich mit dem Betrag eines Vektors beschäftigen. Die Themen Addition und Subtraktion von Vektoren und Skalare Multiplikation – Vielfache von Vektoren bieten weitere spannende Erkenntnisse.
Wenn du das Gelernte direkt anwenden möchtest, dann schau dir gerne den Übungstext zu den Vektoren an.
Zusammenfassung – Was ist ein Vektor?
- Ein Vektor ist ein mathematisches Objekt, das eine Richtung, eine Orientierung und eine Länge hat. Es dient beispielsweise dazu, Verschiebungen (oder in der Physik Bewegungen) zu beschreiben.
- Ein Vektor wird durch einen Vektorpfeil dargestellt, der nicht ortsgebunden ist, also beliebig im Raum verschoben werden kann, solange Richtung, Orientierung und Länge gleich bleiben.
- Ein konkreter Vektorpfeil hat im Koordinatensystem einen Anfangspunkt und einen Endpunkt. Verläuft ein Vektorpfeil beispielsweise vom Punkt $A$ zum Punkt $B$, kann er als $\overrightarrow{AB}$ bezeichnet werden oder mit einem einfachen Buchstaben, z. B. $\vec{a}$.
- Die Länge eines Vektors wird auch als Betrag des Vektors geschrieben, z. B. als $\vert \vec{a} \vert$.
- Vektoren, die sich nur in ihrer Orientierung, nicht aber in Richtung und Betrag unterscheiden, nennt man Gegenvektoren.
Häufig gestellte Fragen zum Thema Was ist ein Vektor?
Transkript Was ist ein Vektor?
In der industriellen Produktion muss jeder Griff sitzen. Aber woher wissen die Roboterarme eigentlich, wohin sie sich bewegen sollen? Das kann man ihnen mit Hilfe von VEKTOREN vorgeben. Bleibt nur die Frage: "Was ist eigentlich ein Vektor?” Vektoren sind die Grundbausteine für das mathematische Teilgebiet der analytischen Geometrie, beziehungsweise der linearen Algebra. Der Begriff "Vektor" kommt aus dem Lateinischen und bedeutet so viel wie "Träger". Wir können uns also als Eselsbrücke merken, dass Vektoren, zum Beispiel dieser hier, Punkte an einen anderen Ort TRAGEN. Der Vektor v trägt Punkt A zum Punkt A-Strich. Er kann aber auch auf alle anderen Punkte im Koordinatensystem angewendet werden und trägt sie dann alle in die gleiche Richtung und über dieselbe Distanz. Der Vektor v kann so zum Beispiel alle Punkte dieses Dreiecks über die gleiche Distanz in die gleiche Richtung verschieben. Der Vektor beschreibt diese Bewegung und wird deshalb im Koordinatensystem durch Vektorpfeile dargestellt. Diese sind alle zueinander parallel, gleich lang und gleich gerichtet. Das heißt, ALLE Vektorpfeile, die dieselbe Bewegung beschreiben, stellen den gleichen Vektor dar. Das führt uns zur ersten großen Erkenntnis: Vektoren sind – anders als Punkte oder Funktionsgraphen – NICHT ortsgebunden. Die beiden Größen, die alle diese Vektorpfeile gemein haben, sind die Länge und die Richtung. Ihre Länge kann man mit dem Satz des Pythagoras bestimmen, aber die RICHTUNG!? Genau DAS ist das Neue und Aufregende an Vektoren. In dieser Schreibweise kann man die Richtung angeben. Dabei ist es wie bei den Koordinaten von Punkten: zuerst geben wir die x-Richtung und danach die y-Richtung an. Um Vektoren und Punkte besser unterscheiden zu können, schreibt man bei Vektoren die Einträge UNTEReinander. Deshalb sagt man auch "Spaltenvektoren". Manchmal liest man auch den Begriff "Tupel" - so wird ein Vektor mit zwei Koordinaten genannt. Einen Vektor mit DREI Koordinaten nennt man Tripel. Na dann machen wir es doch nicht so spannend und schauen uns das Ganze mal im dreidimensionalen Koordinatensystem an. Um die betrachteten Punkte in der Räumlichkeit besser zu verorten, stellen wir sie hier als Eckpunkte von Quadern dar. Wenn wir den Punkt A zum Punkt B verschieben wollen, brauchen wir also den Vektor v, der von A nach B verläuft. Dafür müssen wir eine Einheit nach vorne, zwei Einheiten nach rechts und eine Einheit nach oben wandern. Der Vektor v lautet dann "eins, zwei, eins". Da wir ihn mit Hilfe der Punkte A und B ermittelt haben, nennen wir ihn "Verbindungsvektor von A zu B", kurz: "Vektor A-B". Wie kann man jetzt aber einen Vektor aufstellen, ohne ihn vorher im Koordinatensystem einzuzeichnen? Dafür nehmen wir uns einfach jeweils die Koordinaten des Start- und Endpunktes und subtrahieren diese. Es gilt dabei: "Endpunkt minus Anfangspunkt". Das schreiben wir schön zeilenweise auf und fertig ist der Vektor. Wollen wir allerdings nicht von A nach B, sondern umgekehrt von B nach A verschieben, dann müssen wir den Vektor B-A aufstellen. Dafür rechnen wir dann die Koordinaten von A minus die Koordinaten von B. Der Vektor B-A hat also die Koordinaten "minus eins, minus zwei, minus eins". Das heißt, im Koordinatensystem gehen wir nun von B aus eine Einheit nach hinten, zwei Einheiten nach links und eine Einheit nach unten, um bei A anzukommen. Wir sind auf allen drei Koordinatenachsen also in die negative Richtung gelaufen. Da Vektor B-A genau die gegensätzliche Richtung hat, wird er auch GEGENVEKTOR von A-B genannt. Wir können uns also merken, dass sich beim Gegenvektor nur die Vorzeichen der Koordinaten ändern. Übrigens hat jeder Punkt im Koordinatensystem auch seinen eigenen ORTSVEKTOR. Das ist der Vektor, der vom Koordinatenursprung bis zum entsprechenden Punkt verläuft. Deshalb heißen die Ortsvektoren auch oft O-A oder O-P. Auch hier müssen wir wieder die Koordinaten des Start- und Endpunktes subtrahieren, um auf den gesuchten Vektor zu kommen. Aber nun wird es besonders einfach, denn wegen des Koordinatenursprungs müssen wir hier dreimal Null abziehen. Easy! Wir können uns also merken, dass wir die Lage von Punkten in einem Koordinatensystem auch mithilfe von Ortsvektoren beschreiben können. Der Ortsvektor eines Punktes hat dieselben Koordinaten wie der Punkt, nur wird er eben als Vektor in Spaltenform aufgeschrieben. Es gibt übrigens auch einen Vektor, der eine "Nicht-Bewegung" beschreibt - der sogenannte Null-Vektor. Bei ihm sind alle Einträge Null. Meist wird er mit einem kleinen O bezeichnet. Er hat keine Länge und dadurch auch keine Richtung, weshalb wir ihn auch nicht einzeichnen können. Aber zum Rechnen braucht man eben hin und wieder eine Null und somit ist der NullVEKTOR quasi der Zwillingsbruder der ZAHL Null. Puh, das waren jetzt ganz schön viele Infos - fassen wir das Wichtigste nochmal auf einen Blick zusammen. Vektoren sind unsere neuen Grundbausteine für das Themengebiet der analytischen Geometrie. Sie werden durch Vektorpfeile dargestellt. Jeder Vektor ist durch seine Länge und Richtung definiert. Solange diese beiden Eigenschaften bei verschiedenen Vektorpfeilen gleich sind, können sie überall im Raum platziert werden - es handelt sich trotzdem immer um den GLEICHEN Vektor. Das heißt alle Pfeile, die zu einem Vektor gehören sind zueinander parallel, gleich lang und gleich gerichtet. Die Koordinaten eines Vektors geben an, wie viele Schritte man vom Startpunkt in die jeweiligen Achsenrichtungen gehen muss, um zum Endpunkt zu gelangen. Wir können sie also bestimmen, indem wir "Endpunkt minus Anfangspunkt" rechnen. Bei einem Gegenvektor kehren sich Vorzeichen aller Koordinaten um. Ein Vektorpfeil, der den Koordinatenursprung mit einem bestimmten Punkt verbindet, nennen wir auch Ortsvektor zu dem gegeben Punkt. Und schließlich brauchen wir in der Mathematik auch immer eine Null. In diesem Fall ist das der Nullvektor. Wofür das alles gut sein soll? Naja wenn du selber weißt, wo's lang geht, kannst du es auch dem Roboter sagen!
Was ist ein Vektor? Übung
-
Vervollständige den Text zu Vektoren.
TippsDie Besonderheit von Vektoren ist, dass sie Größen beschreiben, die eine Richtung haben.
Alle drei Vektoren im Bild sind gleich, obwohl sie an verschiedenen Stellen des Koordinatensystems sind. Was ist bei einem Vektor wichtig?
LösungDer Vektor von Punkt $A$ nach $B$ beschreibt im Allgemeinen eine Verschiebung des Punktes $A$ in den Punkt $B$. Sie wird durch einen Pfeil dargestellt, der an jeden beliebigen Punkt angesetzt werden kann. Vektoren sind also nicht ortsgebunden. Solange zwei Vektoren in Länge und Richtung übereinstimmen, sind diese beiden Vektoren gleich. Mithilfe von nur einem Vektoren lassen sich daher Verschiebungen von gesamten Figuren, wie z.B. Dreiecken, beschreiben. Dabei wird jeder Punkt der Figur mit dem Vektor verschoben.
Der Vektor, der von Punkt $A$ zu Punkt $B$ zeigt, wird Verbindungsvektor $\overrightarrow{AB}$ genannt. Außerdem heißt der Vektor $\overrightarrow{BA}$, der genau in die entgegengesetzte Richtung zeigt, Gegenvektor von $\overrightarrow{AB}$. Dieser verbindet ebenfalls die Punkte $B$ und $A$, zeigt aber in die entgegengesetzte Richtung.
-
Gib die richtige Definition der verschiedenen Begriffe an.
TippsJeder Vektor hat eine Länge und eine Richtung und kann als Pfeil dargestellt werden. Die einzige Ausnahme ist der Nullvektor.
Ein Vektor zwischen zwei Punkten beschreibt den Weg, um von einem Punkt zum anderen zu gelangen.
Bei einem Ortsvektor wird der Weg vom Koordinatenursprung zu einem Punkt beschrieben.
LösungEin Ortsvektor $\overrightarrow{OA}$ ist der Vektor, der die Bewegung beschreibt, um vom Koordinatenursprung $O$ zu einem Punkt $A$ zu kommen. Beispielsweise haben wir den Punkt $A$ mit den Koordinaten $A(2 | 4 )$. Da der Koordinatenursprung $O$ die Koordinaten $O(0|0)$ hat, ergibt sich für den Ortsvektor $\overrightarrow{OA} = \begin{pmatrix} 2\\4 \end{pmatrix}$.
Ein Verbindungsvektor $\overrightarrow{AB}$ ist der Vektor, der die Verschiebung von einem Punkt $A$ zu einem Punkt $B$ beschreibt. Er wird durch die Differenz der beiden Ortsvektoren berechnet: $\overrightarrow{AB} = \overrightarrow{OB} - \overrightarrow{OA}$.
Für die konkreten Punkte $A(3|1)$ und $B(1|0)$ ergibt sich beispielsweise der Verbindungsvektor $\overrightarrow{AB}$:$\overrightarrow{AB} = \overrightarrow{OB} - \overrightarrow{OA}= \begin{pmatrix} 1\\0 \end{pmatrix} - \begin{pmatrix} 3\\1 \end{pmatrix} =\begin{pmatrix} -2\\-1 \end{pmatrix}$.
Ein Gegenvektor $\overrightarrow{BA}$ ist der gleiche Vektor wie der Verbindungsvektor $\overrightarrow{AB}$, aber mit umgekehrter Richtung. Das bedeutet, dass er die Bewegung von einem Punkt $B$ zum Punkt $A$ beschreibt. Er entspricht dem Verbindungsvektor mit umgekehrten Vorzeichen: $\overrightarrow{BA}= - \overrightarrow{AB}$.
Der Gegenvektor zu dem Verbindungsvektor $\overrightarrow{AB} = \begin{pmatrix} -2\\-1 \end{pmatrix}$ ist der Vektor: $\overrightarrow{BA}= \begin{pmatrix} 2\\1 \end{pmatrix}$.Der Nullvektor $\vec{o}= \begin{pmatrix} 0 \\ 0 \\ 0\end{pmatrix}$ ist der einzige Vektor, der keine Länge und damit auch keine Richtung besitzt. Man kann ihn nicht zeichnen, da alle seine Koordinaten null sind.
-
Bestimme den Verbindungsvektor.
TippsUm einen Verbindungsvektor zu bestimmen, rechnen wir "Endpunkt minus Anfangspunkt".
Mit "Endpunkt minus Anfangspunkt" sind die Ortsvektoren der jeweiligen Punkte gemeint. Zum Beispiel berechnen wir den Verbindungsvektor zwischen den Punkten $A(0|1)$ und $B(1|4)$ mit:
$\overrightarrow{AB} = \begin{pmatrix} 1 \\ 4 \end{pmatrix} - \begin{pmatrix} 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 1 \\ 3 \end{pmatrix}$.
Ein Ortsvektor ist der Vektor, der von dem Koordinatenursprung $O$ in Richtung des Punktes zeigt. Da aber der Koordinatenursprung die Koordinaten $O(0\vert0)$ hat, sind die Einträge des Ortsvektors einfach die Koordinaten des Punktes selbst.
LösungDer Verbindungsvektor $\overrightarrow{AB}$ zwischen den beiden Punkten $A$ und $B$ wird als Differenz der Ortsvektoren berechnet:
$\overrightarrow{AB} = \overrightarrow{OB} - \overrightarrow{OA}$. Damit wir uns das besser merken, sprechen wir dabei von "Endpunkt minus Anfangspunkt".
Die Ortsvektoren von $A$ und $B$ sind die Vektoren, die vom Koordinatenursprung $O$ in Richtung der jeweiligen Punkte zeigen. Da aber der Koordinatenursprung $O$ die Koordinaten $O(0\vert0)$ besitzt, sind die Ortsvektoren der Punkte einfach die Koordinaten der jeweiligen Punkte selbst.
Das bedeutet, für $\overrightarrow{OA}$ und $\overrightarrow{OB}$ ergibt sich:$ \overrightarrow{OA} = \begin{pmatrix} 5 \\1 \end{pmatrix}$ und $\ \overrightarrow{OB} = \begin{pmatrix} 2 \\4 \end{pmatrix}$.
Insgesamt ergibt das für den Verbindungsvektor
$\overrightarrow{AB} = \begin{pmatrix} 2 \\4 \end{pmatrix} - \begin{pmatrix} 5 \\1 \end{pmatrix} = \begin{pmatrix} 2-5 \\ 4-1 \end{pmatrix}= \begin{pmatrix} -3 \\3 \end{pmatrix}$.
-
Ermittle die Vektoren zu den gegebenen Punkten.
TippsDer Verbindungsvektor $\overrightarrow{AC}$ lässt sich beispielsweise so ausrechnen:
$\overrightarrow{AC} = \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix} - \begin{pmatrix} 2 \\ -2 \\ 1 \end{pmatrix} = \begin{pmatrix} 1-2 \\ 1-(-2) \\ 0-1 \end{pmatrix} = \begin{pmatrix} -1 \\ 3 \\ -1 \end{pmatrix}$
Vertauschen wir die Reihenfolge der Ortsvektoren bei der Differenz, berechnen wir den Gegenvektor von dem Vektor, den wir eigentlich ausrechnen wollen. Zum Beispiel wird mit $\overrightarrow{OA} - \overrightarrow{OB}$ der Gegenvektor $\overrightarrow{BA}$ zu $\overrightarrow{AB}$ berechnet.
Um den Gegenvektor schnell auszurechnen, können wir ausnutzen, dass die Vorzeichen des Verbindungsvektors nur umgedreht werden müssen. Das bedeutet, wir multiplizieren den Verbindungsvektor mit $-1$ und erhalten den Gegenvektor.
LösungMit den gegebenen Punkten $A(2 \vert {-}2 \vert 1)$,$B(0 \vert 3 \vert1)$ und $C(1 \vert 1 \vert 0)$ können wir zunächst die Ortsvektoren der Punkte aufstellen. Diese sind:
$\overrightarrow{OA} = \begin{pmatrix} 2\\-2\\1 \end{pmatrix}$, $\overrightarrow{OB} = \begin{pmatrix} 0\\3\\1 \end{pmatrix}$, $\overrightarrow{OC} = \begin{pmatrix} 1\\1\\0 \end{pmatrix}$.
Anschließend können die verschiedenen Verbindungsvektoren durch die Differenz der Ortsvektoren bestimmt werden. Es gilt:
$\overrightarrow{AB} = \overrightarrow{OB} - \overrightarrow{OA} = \begin{pmatrix} 0\\3\\1 \end{pmatrix} - \begin{pmatrix} 2\\-2\\1 \end{pmatrix} = \begin{pmatrix} 0-2\\3-(-2)\\1-1 \end{pmatrix}= \begin{pmatrix} -2\\5\\0 \end{pmatrix}$,
$\overrightarrow{BA} = \overrightarrow{OA} - \overrightarrow{OB} = \begin{pmatrix} 2\\-2\\1 \end{pmatrix} - \begin{pmatrix} 0\\3\\1 \end{pmatrix} = \begin{pmatrix} 2-0\\(-2) - 3\\1-1 \end{pmatrix} = \begin{pmatrix} 2\\-5\\0 \end{pmatrix}$,
$\overrightarrow{CA} = \overrightarrow{OA} - \overrightarrow{OC} = \begin{pmatrix} 2\\-2\\1 \end{pmatrix} - \begin{pmatrix} 1\\1\\0 \end{pmatrix} = \begin{pmatrix} 2-1\\(-2)-1\\1-0 \end{pmatrix} = \begin{pmatrix} 1\\-3\\1 \end{pmatrix}$,
$\overrightarrow{BC} = \overrightarrow{OC} - \overrightarrow{OB} = \begin{pmatrix} 1\\1\\0 \end{pmatrix} - \begin{pmatrix} 0\\3\\1 \end{pmatrix} = \begin{pmatrix} 1-0\\1-3\\0-1 \end{pmatrix} = \begin{pmatrix} 1\\-2\\-1 \end{pmatrix}$.
Der Vektor $\overrightarrow{BA}$ ist der Gegenvektor zum Verbindungsvektor $\overrightarrow{AB}$. Wir berechnen ihn, indem wir die Ortsvektoren in der Differenz vertauschen. Das ist äquivalent dazu, die Vorzeichen des Verbindungsvektors $\overrightarrow{AB}$ umzudrehen bzw. den Vektor $\overrightarrow{AB}$ mit $-1$ zu multiplizieren.
-
Berechne den Verbindungsvektor zwischen den Punkten $A$ und $B$.
TippsDer Verbindungsvektor $\overrightarrow{AB}$ ist der Vektor, der von Punkt $A$ in Richtung des Punktes $B$ zeigt.
Der Verbindungsvektor $\overrightarrow{AB}$ wird durch die Differenz der Ortsvektoren von $A$ und $B$ berechnet. Es gilt also: $ \overrightarrow{AB} = \overrightarrow{OB} - \overrightarrow{OA}$.
Die Formel zum Berechnen des Verbindungsvektors $\overrightarrow{AB}$ kannst du dir gut merken, indem du "Endpunkt minus Anfangspunkt" rechnest.
LösungDer Verbindungsvektor $\overrightarrow{AB}$ ist der Vektor, der von Punkt $A$ in Richtung des Punktes $B$ zeigt. Er wird durch die Differenz der Ortsvektoren von $A$ und $B$ berechnet. Das bedeutet, es gilt: $\overrightarrow{AB} = \overrightarrow{OB} - \overrightarrow{OA}$.
Diese Formel kannst du dir gut merken, indem du dir "Endpunkt minus Anfangspunkt" einprägst.Für den Verbindungsvektor $\overrightarrow{AB}$ zwischen den Punkten $A(2\vert2\vert2)$ und $B(3\vert 4 \vert 3)$ ergibt sich:
$\overrightarrow{AB} = \overrightarrow{OB} - \overrightarrow{OA} = \begin{pmatrix} 3\\ 4\\3 \end{pmatrix} - \begin{pmatrix} 2\\ 2\\2 \end{pmatrix} = \begin{pmatrix} 3 - 2\\ 4 - 2\\3 - 2 \end{pmatrix} = \begin{pmatrix} 1\\ 2\\1 \end{pmatrix}$. -
Entscheide, ob die Aussagen zu den Vektoren der Pyramide zutreffen.
TippsEs gibt drei korrekte Antworten.
Um dir die Koordinaten der Pyramide besser vorzustellen, solltest du versuchen, sie in einem dreidimensionalen Koordinatensystem zu zeichnen.
Zwei Vektoren sind dann gleich, wenn sie in Länge und Richtung übereinstimmen. Das heißt, dass sie gleich sein können, obwohl sie zwei unterschiedliche Kanten der Pyramide beschreiben.
LösungBei der Pyramide ist der Eckpunkt $D$ der Koordinatenursprung, was das Untersuchen der Antworten vereinfacht. Bevor wir damit anfangen, muss klar sein, dass zwei Vektoren nur gleich sind, wenn sie in Länge und Richtung übereinstimmen. Sie sind nicht ortsgebunden und können von jedem Punkt ausgehen.
Wir überprüfen, ob die einzelnen Antworten bei der Aufgabe stimmen:
Antwort 1: Der Ortsvektor $\overrightarrow{OD}$ ist der Nullvektor $\vec{o} = \begin{pmatrix} 0\\0\\0\end{pmatrix}$.
Der Eckpunkt $D$ der Pyramide liegt hier direkt im Koordinatenursprung. Der Ortsvektor ist der Nullvektor. Diese Antwort stimmt.Antwort 2: Der Verbindungsvektor $\overrightarrow{AE}$ ist $\overrightarrow{AE} = \begin{pmatrix} -1 \\ 1 \\ 2 \end{pmatrix}$.
Die Antwort ist korrekt. Den Verbindungsvektor berechnen wir mit: $\overrightarrow{AE} = \begin{pmatrix} 1 \\ 1 \\ 2 \end{pmatrix} - \begin{pmatrix} 2 \\0 \\ 0 \end{pmatrix} = \begin{pmatrix} -1 \\ 1 \\ 2 \end{pmatrix}$.Antwort 3: Die Verbindungsvektoren $\overrightarrow{AD}$ und $\overrightarrow{BC}$ sind gleich.
Diese Antwort stimmt, denn die beiden Vektoren stimmen in Länge und Richtung überein. Es gilt:
$ \overrightarrow{AD} = \overrightarrow{BC} = \begin{pmatrix} -2 \\ 0 \\ 0 \end{pmatrix}$.Antwort 4: Der Vektor $\overrightarrow{DA}$ ist der Gegenvektor zum Verbindungsvektor $\overrightarrow{CB}$.
Der Vektor $\overrightarrow{DA} =\begin{pmatrix} 2 \\ 0 \\ 0 \end{pmatrix} $ und der Vektor $\overrightarrow{CB} = \begin{pmatrix} 2 \\ 0 \\ 0 \end{pmatrix} $ unterscheiden sich nicht nur um den Faktor ${-}1$. Der Vektor $\overrightarrow{DA}$ ist nicht der Gegenvektor. Die beiden Vektoren sind hier identisch. Diese Aussage ist nicht korrekt.Antwort 5: Der Verbindungsvektor $\overrightarrow{BE}$ ist $\overrightarrow{BE} = \begin{pmatrix} 1 \\ 1 \\ -2 \end{pmatrix}$.
Die Antwort stimmt nicht. Den Verbindungsvektor berechnen wir mit: $\overrightarrow{BE} = \begin{pmatrix} 1 \\ 1 \\ 2 \end{pmatrix} - \begin{pmatrix} 2 \\2 \\ 0 \end{pmatrix} = \begin{pmatrix} -1 \\ -1 \\ 2 \end{pmatrix}$.Antwort 6: Der Ortsvektor $\overrightarrow{OC}$ ist der Gegenvektor zum Ortsvektor $\overrightarrow{OA}$.
Der Ortsvektor $\overrightarrow{OC} =\begin{pmatrix} 0 \\ 2 \\ 0 \end{pmatrix} $ ist nicht der Gegenvektor des Ortsvektors $\overrightarrow{OA} = \begin{pmatrix} 2 \\ 0 \\ 0 \end{pmatrix} $, da sie sich nicht um den Faktor ${-}1$ unterscheiden. Diese Aussage ist nicht korrekt.
9.706
sofaheld-Level
6.600
vorgefertigte
Vokabeln
7.841
Lernvideos
37.238
Übungen
32.624
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Schulstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung





 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?














Ja für die 7 Klasse wäre cool
Was genau sind dimension
Könntet ihr vielleicht auch noch ein Video dazu für die 7. Klasse machen?