Stammfunktionen berechnen
Eine Stammfunktion ist eine Funktion $F$, deren Ableitung $f$ entspricht. Im Gegensatz zur Ableitung gibt es für eine Stammfunktion $F$ unendlich viele Lösungen ($F(x) + c$). Erfahre, wie man Stammfunktionen graphisch darstellt und wofür sie verwendet werden! Interessiert? Das und vieles mehr findest du im folgenden Text.
- Stammfunktion – Definition
- Grafische Darstellung von Stammfunktion und Ableitungsfunktion
- Ableitungsfunktion – grafische Darstellung
- Stammfunktion – grafische Darstellung


in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.

Grundlagen zum Thema Stammfunktionen berechnen
Stammfunktion – Definition
In Mathe hast du bestimmt schon die Ableitung einer Funktion kennengelernt. Nun klären wir, was die Stammfunktion einer Funktion ist. Die beiden hängen nämlich direkt miteinander zusammen.
Eine Stammfunktion zu einer gegebenen Funktion $f(x)$ ist eine Funktion, die wir allgemein als $F(x)$ bezeichnen und deren Ableitung die Funktion $f(x)$ ergibt. Als Formel geschrieben können wir das so ausdrücken:
$F^{\prime}(x) = f(x)$
Wenn du eine Ableitung bilden sollst, ist normalerweise eine Funktion $f(x)$ gegeben und ihre Ableitung $f^{\prime}(x)$ gesucht. Bei der Frage nach einer Stammfunktion ist es umgekehrt: Die Ableitung ist gegeben und die Funktion ist gesucht.
- Die Ableitung einer Funktion $f(x)$ bezeichnen wir als $f^{\prime}(x)$. Die Stammfunktion einer Funktion $f(x)$ wird üblicherweise mit $F(x)$ benannt.
- Bei der Berechnung der Ableitung einer Funktion $f(x)$ gibt es nur eine richtige
Lösung – vorausgesetzt, die Funktion $f(x)$ ist überhaupt differenzierbar. Bei der Bestimmung einer Stammfunktion $F(x)$ gibt es hingegen nie nur eine richtige Lösung:
Ist $F(x)$ eine Stammfunktion von $f(x)$, so ist auch $F(x)+c$ eine Stammfunktionvon $f(x)$. Hierbei ist $c \in \mathbb{R}$ eine konstante reelle Zahl.
Den letzten Punkt können wir direkt nachrechnen und beweisen. Berechnen wir die Ableitung der Funktion $F(x)+c$, so erhalten wir:
$\left( F(x) + c \right)^{\prime} = F^{\prime}(x) + c^{\prime} = F^{\prime}(x) + 0 = F^{\prime}(x) = f(x)$
Da die Ableitung einer beliebigen konstanten Zahl $c$ stets null ist $\left( c^{\prime} = 0 \right)$, gibt es unendlich viele Stammfunktionen $F(x) + c$ mit $c \in \mathbb{R}$, deren Ableitung die Funktion $f(x)$ ergibt. Man spricht in diesem Zusammenhang von einer Schar von Stammfunktionen.
Fehleralarm
Ein häufiger Fehler beim Thema Stammfunktionen ist die Annahme, dass die Konstante $c$ weggelassen werden kann. Die Konstante $c$ ist jedoch ein wichtiger Faktor für die Ermittlung der allgemeinen Stammfunktion. Schülerinnen und Schüler sollten dies immer im Hinterkopf haben.
Grafische Darstellung von Stammfunktion und Ableitungsfunktion
Im Folgenden sehen wir uns an, was der Zusammenhang zwischen Stammfunktion und Ableitungsfunktion hinsichtlich der jeweiligen Funktionsgraphen bedeutet. Dazu wiederholen wir zuerst, was den Graphen einer Ableitungsfunktion kennzeichnet.
Ableitungsfunktion – grafische Darstellung
Im Koordinatensystem bildet der Funktionsgraph der Ableitung $f^{\prime}(x)$ die Steigung des Funktionsgraphen der ursprünglichen Funktion $f(x)$ ab.
Um das darzustellen, lesen wir an jedem Punkt $x$ den Wert der Steigung von $f(x)$ ab (bzw. berechnen diesen) und tragen diesen Wert als Funktionswert der Ableitung $f^{\prime}(x)$ ein.
- An jeder Stelle $x$, an der die Funktion $f(x)$ ansteigt, ist die Ableitung $f^{\prime}(x)$ positiv.
- An Stellen, an denen $f(x)$ eine horizontale Tangente hat, hat $f^{\prime}(x)$ eine Nullstelle. Dort hat die Steigung von $f(x)$ also den Wert $0$.
- An allen Stellen $x$, an denen $f(x)$ abfällt, ist die Ableitung $f^{\prime}(x)$ negativ.
Zeichnen wir zu dem Funktionsgraphen von $f(x)$ noch die Funktionsgraphen der Funktionen $f(x)+2$ und $f(x)-3$, so finden wir zu allen drei Funktionen dieselbe Ableitungsfunktion $f^{\prime}(x)$. Denn die Funktionen $f(x)+2$ und $f(x)-3$ stellen lediglich eine Verschiebung der Funktion $f(x)$ entlang der
Da sich $f(x)$, $f(x)+2$ und $f(x)-3$ nur durch die Addition einer konstanten, reellen Zahl $c$ unterscheiden, gehören all diese Funktionen zur Schar der Stammfunktionen in Bezug auf die Ableitungsfunktion $f^{\prime}(x)$. Es gilt:
$\left( f(x) \right)^{\prime} = \left( f(x)+2 \right)^{\prime} = \left( f(x)-3 \right)^{\prime} = f^{\prime}(x)$
Wir können nun unsere Perspektive wechseln und die Ableitungsfunktion $f^{\prime}(x)$ als eigentliche Funktion $f(x)$ benennen. Dann müssen wir die vorherigen Funktionen $f(x)$, $f(x)+2$ und $f(x)-3$ eindeutig als Stammfunktionen kennzeichnen. Wir nennen sie also $F(x)$, $F(x)+2$ und $F(x)-3$. Damit gilt:
$\left( F(x) \right)^{\prime} = \left( F(x)+2 \right)^{\prime} = \left( F(x)-3 \right)^{\prime} = f(x)$
Achtung! Dieser Perspektivwechsel ändert nichts an den Zusammenhängen der Funktionen und Funktionsgraphen – wir haben nur die Benennung, also die Buchstaben, geändert. Die Beziehung zwischen $f(x)$ und $f^{\prime}(x)$ haben wir einfach umbenannt zu $F(x)$ und $f(x)$.
Stammfunktion – grafische Darstellung
Zu einer gegebenen Funktion $f(x)$ den Funktionsgraphen der Stammfunktion $F(x)$ zu zeichnen, ist deutlich schwieriger als der umgekehrte Weg. Dazu müssen wir an jeder Stelle $x$ den Funktionswert $F(x)$ so einzeichnen, dass die Steigung des Funktionsgraphen von $F(x)$ an der Stelle $x$ genau dem Funktionswert $f(x)$ entspricht. Das ist gar nicht so einfach, aber wir können uns dabei zumindest an den Nullstellen der Funktion $f(x)$ orientieren:
- Ist $f(x) = 0$ an einer Stelle $x$, so hat jede Stammfunktion an dieser Stelle eine horizontale Tangente.
- Ist $f(x)$ links der Nullstelle positiv, so steigt jede Stammfunktion $F(x)$ dort an.
- Ist $f(x)$ rechts der Nullstelle negativ, so fällt jede Stammfunktion dort ab.
- Nähern sich die Funktionswerte von $f(x)$ der
$x$-Achse an, so nähert sich auch jede Stammfunktion einem konstanten Funktionswert an, nämlich dem Wert $c$.
Unter Berücksichtigung dieser Punkte können wir mögliche Stammfunktion zu einer gegebenen Funktion $f(x)$ zeichnen. In der folgenden Abbildung siehst du drei mögliche Stammfunktionen zu einer Funktion $f(x)$. Es handelt sich bei den Stammfunktionen um die Funktionen $F(x)$, $F(x)+2$ und $F(x)-3$, die wir auch schon im Rahmen der Betrachtung der Ableitungsfunktion untersucht haben.
Die Abbildung ist sowohl gültig, wenn wir $f(x)$ (unten) gegeben haben und mögliche Stammfunktionen (oben) einzeichnen sollen, als auch, wenn wir eine der drei Stammfunktionen (oben) gegeben haben und die zugehörige Ableitungsfunktion $f(x)$ (unten) einzeichnen sollen – denn in beiden Fällen gilt:
$\left( F(x) \right)^{\prime} = \left( F(x)+2 \right)^{\prime} = \left( F(x)-3 \right)^{\prime} = f(x)$
Haben wir eine Stammfunktion $F(x)$ gefunden, so sind auch die Funktionen $F(x)+2$ und $F(x)-3$ Stammfunktionen der Funktion $f(x)$. Die Stammfunktion $F(x)$ ist also nicht eindeutig bestimmt durch die Funktion $f(x)$ – jede konstante Verschiebung des Funktionsgraphen einer Stammfunktion $F(x)$ um den Wert $c$ in
In unserem Beispiel haben wir einmal $c = 2$ und einmal $c = -3$ gewählt, um das zu verdeutlichen.
Kennst du das?
Wenn du einen Berg hinauf steigst, kannst du die Steigung direkt spüren – aber nicht die genaue Höhe, auf der du dich befindest. Ob du zwei Meter höher oder drei Meter tiefer bist, kannst du nicht unmittelbar feststellen. Die tatsächliche Höhe hängt auch davon ab, wo der Nullpunkt der Höhenskala liegt – die Steigung hängt davon nicht ab, sondern lässt sich unmittelbar beobachten.
Die Steigung entspricht in diesem Beispiel der vorgegebenen Funktion $f(x)$, die tatsächliche Höhe, auf einer geeigneten Skala gemessen, ist eine Stammfunktion $F(x)+c$ mit einem beliebigen Wert $c \in \mathbb{R}$.
Stammfunktionen berechnen
Stammfunktionen müssen nicht immer grafisch ermittelt werden. Eine Stammfunktion zu einer Funktion $f(x)$ kann auch rechnerisch bestimmt werden, wenn der Funktionsterm von $f(x)$ bekannt ist. Das Berechnen von Stammfunktionen heißt auch Integrieren.
Ein Integral ist eine bestimmte Stammfunktion einer gegebenen Funktion. Ein sogenanntes unbestimmtes Integral schließt die Gesamtheit aller Stammfunktionen ein, die es zu einer gegebenen Funktion gibt. Das schreibt man so:
$\displaystyle \int f(x) ~\text{d}x = F(x) + c \quad$ mit $\quad c \in \mathbb{R}$
Darin sind
- $\int$ das Integralzeichen,
- $\text{d}x$ das Differential $\left(\Delta x \rightarrow 0 \right)$,
- $x$ die Integrationsvariable und
- $f(x)$ der Integrand.
$F(x) + c$ ist die Funktionenschar von Stammfunktionen mit beliebiger Integrationskonstante $c \in \mathbb{R}$, die jeweils abgeleitet die Funktion $f(x)$ ergeben.
Das Integralzeichen bedeutet also, das die Funktion $f(x)$ integriert werden muss, um eine Stammfunktion $F(x) + c$ zu erhalten.
Stammfunktionen berechnen – Beispiel
Gegeben sei die Funktion $f(x) = 3\,x^2$. Wie lautet eine Stammfunktion zu $f(x)$?
Eine mögliche Stammfunktion ist $F(x) = x^3$, denn es gilt:
$F^{\prime}(x) = \left( x^3 \right)^{\prime} = 3 \cdot x^{3-1} = 3\,x^2 = f(x)$
Aber auch die Funktion $F_{-3} = x^3 -3$ wäre eine passende Stammfunktion, denn es gilt ebenso:
${F_{-3}}^{\prime}(x) = \left( x^3 - 3 \right)^{\prime} = 3 \cdot x^{3-1} - 0 = 3\,x^2 = f(x)$
Stammfunktionen berechnen – Rechenregeln
So wie es bestimmte Ableitungsregeln gibt, so gibt es auch für das Integrieren bestimmte Rechenregeln, die je nach Art der Funktion $f(x)$ angewendet werden können, um eine Stammfunktion $F(x)$ zu berechnen. Das sind beispielsweise
- die Potenzregel für Integrale,
- die Faktor- und Summenregel für Integrale,
- die lineare Substitutionsregel für Integrale,
- Regeln für Stammfunktionen von Wurzelfunktionen und
- die logarithmische Integration.
Sehen für uns die Potenzregel für Integrale, also die Regel für Potenzfunktionen, genauer an. Beim Ableiten einer einfachen Potenzfunktion der Form $f(x) = x^n$ wird der Exponent $n$ als Faktor nach vorne gezogen und in der Potenz um Eins erniedrigt. Es gilt also:
$f^{\prime}(x) = \left( x^n \right)^{\prime} = n \cdot x^{n-1}$
Beim Integrieren einer Potenzfunktion $f(x) = x^n$ muss nun genau der umgekehrte Vorgang passieren. Das heißt, der Exponent $n$ wird um Eins erhöht und der Kehrwert des erhöhten Exponenten muss als Faktor nach vorne gezogen werden, damit der Faktor beim Ableiten wegfällt. Allgemein gilt also folgende Regel:
$\displaystyle \int f(x) ~\text{d}x = \displaystyle \int x^n ~\text{d}x = \frac{1}{n +1} \cdot x^{n+1} + c = F(x) + c$
Denn dann gilt umgekehrt:
$F^{\prime}(x) = \left( \dfrac{1}{n +1} \cdot x^{n+1} + c \right)^{\prime} =\dfrac{1}{n +1} \cdot (n+1) \cdot x^{n+1-1} + 0 = x^n = f(x)$
Beachte: Diese Potenzregel für Integrale gilt auch für $n < 0$, allerdings nicht für $n = -1$, denn dann ist der Bruch $\frac{1}{n+1}$ nicht definiert. Dieser Fall ist ein Spezialfall, für den du die korrekte Stammfunktion auswendig lernen solltest. Es gilt:
$\displaystyle \int x^{-1} ~\text{d}x = \displaystyle \int \frac{1}{x} ~\text{d}x = \ln \vert x \vert + c$
Die Stammfunktion zur Funktion $\frac{1}{x}$ ist die natürliche Logarithmusfunktion des Betrags von $x$, also $\ln \vert x \vert$.
Wenden wir die Potenzregel für Integrale einmal systematisch für die ganzrationale Funktion $x^5$ an:
$\displaystyle \int x^5 ~\text{d}x = \frac{1}{5+1} \cdot x^{5+1} ~\left( + c \right) = \frac{1}{6}\,x^6 ~\left( + c \right)$
Eine schnelle Probe durch Ableiten beweist, dass wir richtig liegen:
$\left( \dfrac{1}{6}\,x^6 \right)^{\prime} = \dfrac{1}{6} \cdot 6 \cdot x^{6-1} = x^5$
Stammfunktionen berechnen – bestimmte Integrale
Wenn eine Stammfunktion $F(x)$ rechnerisch ermittelt wurde, kann mit dem Hauptsatz der Differenzial- und Integralrechnung ein sogenanntes bestimmtes Integral berechnet werden:
$\displaystyle \int\limits_{a}^{b} f(x) ~\text{d}x = \Bigl[ F(x)\Bigr]_{a}^{b} = F(b) - F(a)$
Ein bestimmtes Integral ist ein Integral, das einen bestimmten, reellen Zahlenwert hat. Dieser Wert wird als Differenz $F(b) - F(a)$ berechnet, wobei $a$ und $b$ zwei reelle Zahlen sind, die die Integrationsgrenzen des bestimmten Integrals darstellen.
Um ein bestimmtes Integral zu berechnen, muss also zuerst eine Stammfunktion berechnet werden und dann die Werte $a$ und $b$ in diese eingesetzt werden, um die Differenz $F(a) - F(b)$ berechnen zu können. Das Ergebnis der Differenz ist der Wert des bestimmten Integrals in den Grenzen des Intervalls $[a,b]$.
Beispiel:
$\displaystyle \int\limits_{1}^{0} 3\,x^2 ~\text{d}x = \Bigl[ x^3 \Bigr]_{0}^{1} = 1^3 - 0^3 = 1$
Eine wichtige Anwendung von Stammfunktionen und insbesondere von bestimmten Integralen ist die Berechnung von Flächen sowie von anderen Größen, die grafisch durch Flächen ausgedrückt werden können.
So wie die Ableitung der Steigung eines Funktionsgraphen entspricht, so entspricht das Integral der Fläche, die ein Funktionsgraph mit der
Oft wird eine bestimmte Fläche unter dem Graphen in einem Intervall $[a,b]$, also zwischen zwei Grenzen $a$ und $b$, betrachtet.
Hat man beispielsweise das Geschwindigkeits-Zeit-Diagramm
Wusstest du schon?
Wenn du beim Laufen eine Smartwatch trägst, die deine Geschwindigkeit erfasst hat, dann benutzt die Smartwatch das Wissen über Stammfunktionen, um Aussagen und Vorhersagen über die zurückgelegte Strecke zu treffen.
Ausblick – das lernst du nach Stammfunktionen berechnen
Die Rechenregeln für Integrale wie die Potenzregel oder die Faktor- und Summenregel sind die nächsten Schritte. Lerne außerdem, wie du bestimmte Integrale und Flächeninhalte bestimmen kannst!
Oder du übst zunächst erstmal die Integralrechnung und das Bilden von Stammfunktionen in unserem Übungstext.
Zusammenfassung – Stammfunktion
- Eine Stammfunktion einer gegebenen Funktion $f(x)$ ist eine Funktion $F(x)$, die abgeleitet die Funktion $f(x)$ ergibt. Es gilt:
$F^{\prime}(x) = f(x)$ - Funktionsgraphen von Stammfunktionen können grafisch ermittelt werden, wenn eine Funktion $f(x)$ als Darstellung der Steigung einer zugehörigen Stammfunktion $F(x)$ interpretiert wird.
- Ähnlich zu den Ableitungsregeln gibt es auch Rechenregeln für das Integrieren einer Funktion $f(x)$, mit denen eine zugehörige Stammfunktion $F(x)$ berechnet werden kann. Man schreibt:
$\displaystyle \int f(x) ~\text{d}x = F(x) + c \quad$ mit $\quad c \in \mathbb{R}$ - $\displaystyle \int f(x) ~\text{d}x$ ist das unbestimmte Integral der Funktion $f(x)$.
Es bezeichnet die Gesamtheit aller Stammfunktionen $F(x) + c$ mit der Integrationskonstante $c \in \mathbb{R}$, die jeweils abgeleitet die Funktion $f(x)$ ergeben. - Über den Hauptsatz der Differential- und Integralrechnung kann ein bestimmtes Integral in den Grenzen $a$ und $b$ berechnet werden, wenn eine Stammfunktion $F(x)$ zu $f(x)$ bestimmt wurde. Es gilt:
$\displaystyle \int\limits_{a}^{b} f(x) ~\text{d}x = \Bigl[ F(x)\Bigr]_{a}^{b} = F(b) - F(a)$
Häufig gestellte Fragen zum Thema Stammfunktion
Transkript Stammfunktionen berechnen
Fragst du dich auch manchmal, von wem du eigentlich abstammst? Bis zu deinen Großeltern ist ja wahrscheinlich noch alles klar, aber wer waren eigentlich deren Vorfahren? Wo haben sie gelebt? Was haben sie gemacht? Und war eventuell sogar eine berühmte Persönlichkeit unter ihnen? Stammbaumforschung kann echt spannend sein! So, oder so ähnlich kannst du dir auch deine Aufgabe im Matheunterricht das nächste mal schönreden, wenn du „Stammfunktionen“ bestimmen sollst. Denn bei der Bestimmung von Stammfunktionen geht es im Prinzip um genau das. Wir wollen herausfinden, von welchen Funktionen eine gegebene Funktion abstammt. Aber was genau meint „Abstammen“ in diesem Kontext? Um das zu verstehen, gehen wir zunächst einen Schritt zurück und schauen uns nochmal kurz an, wie das aussah, wenn wir Funktionen abgeleitet haben. Wenn wir eine Funktion „f von x“ abgeleitet haben, haben wir die Ableitungsfunktion „f-Strich von x“ genannt. In diesem Sinne stammt also f-Strich von f ab. Jetzt können wir das Ganze aber auch andersherum betrachten und uns überlegen, welche Funktion wir eigentlich ableiten müssen, um „f von x“ zu erhalten. Wir fragen uns also, von welcher Funktion „f von x“ abstammen könnte und nennen eine solche Funktion dann Stammfunktion. Stammfunktionen benennt man üblicherweise mit Großbuchstaben. In unserem Fall wäre das dann „Groß-F von x“. Eine Stammfunktion „Groß-F von x“ der Funktion „f von x“ ist also genau so definiert, dass ihre Ableitung gleich „f von x“ ist. Daher können wir „f von x“ auch als Stammfunktion von „f-Strich von x“ betrachten. Genug Theorie! Wir brauchen ein konkretes Beispiel! Wir betrachten „f von x gleich x Quadrat“. Anstatt diese Funktion jetzt abzuleiten, suchen wir eine Funktion die abgeleitet „x hoch zwei“ ergibt. Das nennen wir „die Funktion integriert“. Da sich beim Ableiten der Exponent um eins verringert, muss die gesuchte Stammfunktion den Exponenten drei haben. Wenn wir „x hoch drei“ ableiten, erhalten wir aber „drei x hoch zwei“. Um diese Drei loszuwerden, multiplizieren wir unsere Stammfunktion noch mit dem Kehrwert von drei – also einem Drittel. Wenn wir diese Funktion jetzt ableiten, kürzen sich drei und ein Drittel weg. Und schon haben wir eine Stammfunktion gefunden. Sprich: Wir haben „f von x“ integriert. Das ist allerdings nicht die einzige Stammfunktion zu unserer Funktion „x Quadrat“. Auch die Funktionen „ein Drittel x hoch drei plus eins“, oder „ein Drittel x hoch drei minus zwei“ sind Stammfunktionen von „f von x“. Denn auch wenn wir diese Funktionen ableiten, erhalten wir wieder „x Quadrat“. Konstanten werden ja beim Ableiten zu Null, fallen also einfach weg. Daher können wir eine beliebige konstante Zahl addieren oder auch subtrahieren. Das Resultat wird immer eine Stammfunktion von „x Quadrat“ sein. Das wird auch deutlich, wenn wir uns die zugehörigen Funktionsgraphen in zwei untereinander liegenden Koordinatensystemen anschauen. „f von x“ gibt als Ableitungsfunktion der Stammfunktionen deren Steigung an jeder beliebigen Stelle wieder. Die Steigung ist erst positiv, dann flacht die Funktion ab, bis die Steigung Null erreicht wird, und schließlich wird die Steigung wieder positiv und immer steiler. Die Steigung von „Groß-F von x“ ändert sich aber nicht, wenn wir die Funktion im Koordinatensystem nach oben oder unten, sprich in y-Richtung verschieben. Und genau das machen wir ja, wenn wir eine beliebige konstante Zahl addieren, beziehungsweise subtrahieren. Umgangssprachlich könnte man sagen: Wie hoch oder tief eine Funktion im Koordinatensystem platziert ist, ist für die Ableitung egal. Diese Information geht durch das Ableiten verloren. Es kommt nur auf die Steigung an. Aus umgekehrter Perspektive kommt daher also auch nicht nur eine Funktion als Stammfunktion in Frage, sondern es gibt eben unendlich viele – die sich alle nur durch eine konstante Zahl unterscheiden. Diese Zahl, auch Integrationskonstante genannt, wird allgemein meistens mit einem c dargestellt. C ist dann eine beliebige, reelle Zahl. Bleibt nur noch eine Frage: Wie berechnen wir denn Stammfunktionen jetzt ganz konkret? Durch Ausprobieren? Zum Glück gibt es – genauso wie beim Ableiten – einige Regeln, an die wir uns halten können. Hier siehst du die wichtigsten schonmal auf einen Blick! Wie genau sie funktionieren und was es mit diesem merkwürdigen Integralzeichen auf sich hat, erfährst du in den entsprechenden Videos. Fürs Erste fassen wir zusammen, was wir über Stammfunktionen gelernt haben. Eine Stammfunktion „Groß-F von x“ zu einer gegebenen Funktion „f von x“ ist so definiert, dass ihre Ableitung gleich „f von x“ ist. Wenn wir eine Stammfunktion zu einer gegebenen Funktion bestimmen, nennen wir das „die Funktion integrieren“. Im Gegensatz zum Ableiten, das eindeutig zu einer Ableitungsfunktion führt, kommen beim Integrieren unendlich viele Stammfunktionen in Frage, da wir nichts über Konstanten wissen können, die beim Ableiten wieder wegfallen würden. Eine Funktion hat also unendlich viele Eltern! Unendlich viele Vorfahren haben wir als Menschen zwar nicht, aber dafür unterscheiden sich unsere Vorfahren etwas deutlicher voneinander – jeder einzelne ist ganz besonders!
Stammfunktionen berechnen Übung
-
Gib an, welche der Aussagen über Stammfunktionen richtig sind.
TippsBeispiel:
Wenn $f(x)=x^5$, dann muss $F(x)$ den Exponenten $6$ haben. Es gilt somit:
$F(x)=\dfrac{1}{6}x^6$, denn:
$\left(\dfrac{1}{6}x^6\right)^\prime = \dfrac{1}{6}\cdot6x^5 = x^5$
LösungAllgemein gilt:
- Wir können eine Funktion ableiten und erhalten die Ableitungsfunktion $f'(x)$.
- Wir können eine Funktion integrieren und erhalten die Stammfunktion $F(x)$.
Die Ableitung der Stammfunktion ist dann gleich $f(x)$. Formal können wir das so schreiben:
$F'(x) = f(x)$
Die Stammfunktion der Ableitung $f^\prime(x)$ ist demnach gleich $f(x)$.
Beim Bilden der Stammfunktion erhöhen wir den Exponenten um $1$, da er sich beim Ableiten um diesen Wert verringert. Außerdem multiplizieren wir mit dem Kehrwert des neuen Exponenten, um den Vorfaktor beim Ableiten auszugleichen.
Um zu festzustellen, ob eine Funktion tatsächlich eine Stammfunktion ist, können wir sie ableiten und überprüfen, ob sie gleich der Ursprungsfunktion ist. Dabei ist zu beachten, dass Konstanten (Terme ohne die Variable $x$) beim Ableiten wegfallen. Dadurch gibt es keine eindeutige Stammfunktion, sondern unendlich viele verschiedene, weil wir eine beliebige reelle Konstante zur Stammfunktion addieren oder subtrahieren können.Folgende Aussagen sind korrekt:
- $F(x)$ ist eine Stammfunktion von $f(x)$, wenn $F'(x)=f(x)$ gilt.
- Wenn $f(x)$ integriert wird, dann entsteht $F(x)$.
- Es gibt unendlich viele verschiedene Stammfunktionen für die Funktion $f(x) = x^2$.
Folgende Aussagen sind inkorrekt:
- $f(x)$ ist die Stammfunktion von $F(x)$.
- Wenn $f(x)$ abgeleitet wird, dann entsteht $F(x)$.
- Die Stammfunktion von $f(x) = x^2$ lautet $F(x) = x^3$, weil der Exponent um $1$ erhöht wird.
-
Beschreibe die Bedeutung der Integrationskonstante $c$.
TippsDer Graph von $x^2 -3$ ist im Vergleich zur Normalparabel ($x^2$) um drei Einheiten nach unten verschoben.
Die Ableitungsfunktion beschreibt die Steigung des Funktionsgraphen.
LösungEine Stammfunktion $F$ ist die Funktion, die abgeleitet wieder $f$ ergibt. Die Funktion $f$ ist also die Steigung von $F$. Wir können schreiben:
$F^\prime(x) = f(x)$
Wird zu einem Funktionsterm eine Konstante addiert, so bewirkt dies eine Verschiebung des Funktionsgraphen in $\boldsymbol{y}$-Richtung.
Die Steigung des Funktionsgraphen für einen $x$-Wert bleibt nach Addition einer Konstante unverändert. Daher sind alle Funktionen, die sich nur durch die Integrationskonstante $c$ unterscheiden, Stammfunktionen derselben Ausgangsfunktion.
Es gilt:
$\left(F(x) + c\right)^\prime = F^\prime(x)$ für alle $c \in \mathbb{R}$
-
Bestimme, welche Ausgangsfunktion zu der jeweiligen Stammfunktion gehört.
TippsEs gibt zu jeder Funktion $f(x)$ unendlich viele Stammfunktionen, die sich nur durch die Integrationskonstante $c$ unterscheiden.
Beispiel:
$f(x)=x^2$
Zwei Stammfunktionen von $f$ lauten:
$F(x)=\dfrac{1}{3}x^3-1$ und ${F(x)=\dfrac{1}{3}x^3+5}$
LösungBei dieser Aufgabe solltest du jede Stammfunktion der passenden Ausgangsfunktion zuordnen.
Die Potenzregel zum Bilden der Stammfunktion lautet:
$f(x) = a \cdot x^n \quad \implies \quad {F(x) = \dfrac{a}{n+1}x^{n+1} + c \quad (c \in \mathbb{R})}$
Beispiel:
Um die Stammfunktion der Funktion $f(x)=x^4$ zu bestimmen, erhöhen wir den Exponenten um $1$. Die Potenz lautet dann also $x^{4+1}=x^5$.
Um den Vorfaktor $5$, der beim Ableiten entsteht, auszugleichen, müssen wir noch mit $\frac{1}{5}$ multiplizieren. Eine mögliche Stammfunktion $F$ lautet also:$F(x) = \dfrac{1}{5}x^5$
Zu dieser Stammfunktion können wir nun eine beliebige reelle Zahl als Integrationskonstante addieren – sie bleibt trotzdem eine Stammfunktion von $f$.
Beachte, dass die Integrationskonstante $c$ beim Ableiten wegfällt. Suchen wir eine Stammfunktion, wissen wir daher nicht, welches $c$ vorhanden war. Deshalb gibt es unendlich viele Möglichkeiten.
Der Funktion $f(x)=3x^3$ können folgende Stammfunktionen zugeordnet werden:
$~\color{#CCCCCC}{\bullet}\color{black}{~}F(x)=\dfrac{3}{4}x^4-1$
$~\color{#CCCCCC}{\bullet}\color{black}{~}F(x)=\dfrac{3}{4}x^4-\dfrac{4}{3}$
$~\color{#CCCCCC}{\bullet}\color{black}{~}F(x)=\dfrac{3}{4}x^4+2$
Denn:
$\left(\dfrac{3}{4}x^4+c\right)^\prime = \dfrac{3}{4} \cdot 4x^3 = 3x^3$
Der Funktion $f(x)=4x^3$ können folgende Stammfunktionen zugeordnet werden:
$~\color{#CCCCCC}{\bullet}\color{black}{~}F(x)=x^4-\dfrac{4}{3}$
$~\color{#CCCCCC}{\bullet}\color{black}{~}F(x)=x^4+2$
Denn:
$\left(x^4+c\right)^\prime = 4x^3$
Der Funktion $f(x)=5x^3$ können folgende Stammfunktionen zugeordnet werden:
$~\color{#CCCCCC}{\bullet}\color{black}{~}F(x)=\dfrac{5}{4}x^4-1$
$~\color{#CCCCCC}{\bullet}\color{black}{~}F(x)=\dfrac{5}{4}x^4+2$
$~\color{#CCCCCC}{\bullet}\color{black}{~}F(x)=\dfrac{5}{4}x^4+\dfrac{1}{4}$
Denn:
$\left(\dfrac{5}{4}x^4+c\right)^\prime = \dfrac{5}{4} \cdot 4x^3 = 5x^3$
-
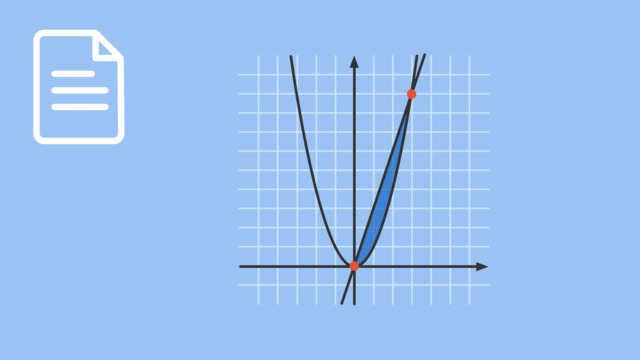
Ermittle den Verlauf des Graphen der Stammfunktion von $f$.
TippsÜberlege dir, welchen Grad die gegebene Funktion hat: Sie zeigt eine Parabel.
Der Graph zeigt eine Funktion zweiten Grades. Daher muss die Stammfunktion eine Funktion dritten Grades sein.
LösungHier haben wir den Graphen einer Funktion zweiten Grades, also eine Parabel, gegeben. Die Funktionsgleichung lautet:
$f(x)=2x^2+4x+1$
Um die Stammfunktion zu bestimmen, erhöhen wir den Exponenten um $1$ und multiplizieren den Term mit dem Kehrwert des Exponenten. Dadurch erhalten wir eine Funktion dritten Grades:
$F(x) = \dfrac{2}{3}x^3 + 2x^2 + x$
Damit können wir alle Graphen von Funktionen, die einen niedrigeren Grad haben (Geraden und Parabeln) ausschließen. Auch der Graph der Funktion mit drei Extremstellen, also die Funktion vierten Grades, können wir ausschließen.
An dem Graph der Ursprungsfunktion sehen wir, dass er die $x$-Achse in den ungefähren Punkten $({-}1{,}7 | 0)$ und $({-}0{,}3 | 0)$ schneidet. Daraus können wir ableiten, dass der Graph der Stammfunktion an diesen Stellen Extremstellen haben muss.
Der erste Graph zeigt eine Funktion dritten Grades, die am Ursprung einen Sattelpunkt hat. Deshalb können wir diese ebenfalls ausschließen und erhalten den oben abgebildeten Graphen.
-
Finde eine Ausgangsfunktion zur Stammfunktion.
TippsBeim Bilden der Stammfunktion erhöht sich der Exponent der Potenz um $1$.
Beispiel:
$F(x)=\dfrac{1}{5}x^5$
Die Ausgangsfunktion $f$ entspricht der Ableitung:
$f(x)= \left(\dfrac{1}{5}x^5\right)^\prime = \dfrac{1}{5}\cdot 5x^4 = x^4$
LösungBei dieser Aufgabe solltest du den Stammfunktionen $F$ ihre Ausgangsfunktionen $f$ zuordnen.
Da zwischen Stammfunktion und Ausgangsfunktion der Zusammenhang $F^\prime(x) = f(x)$ gilt, können wir die Stammfunktionen ableiten und so auf die Ausgangsfunktion schließen.
Die Potenzregel zum Bilden der Stammfunktion lautet:
$f(x) = a \cdot x^n \quad \implies \quad F(x) = \dfrac{a}{n+1}x^{n+1} + c \quad (c \in \mathbb{R})$
Wenn wir die Ableitung von $F$ bilden, dann erhalten wir wieder $f$, weil die Integrationskonstante $c$ wegfällt:
$\left(\dfrac{a}{n+1}x^{n+1} + c\right)^\prime = \dfrac{a}{n+1} \cdot (n+1)x^{n+1-1} = ax^n = f(x)$
Bei den gegebenen Stammfunktionen ist die Integrationskonstante $c=0$ gewählt: Wir leiten sie ab, um die passenden Ausgangsfunktionen zu finden.
Erste Funktion: $F(x)=\dfrac{1}{3}x^3$
$\implies ~ f(x) = \left(\dfrac{1}{3}x^3\right)^\prime = \dfrac{1}{3} \cdot 3 x^2 = \color{#99CC00}{x^2}$
Zweite Funktion: $F(x)=\dfrac{1}{4}x^4$
$\implies ~ f(x) = \left(\dfrac{1}{4}x^4\right)^\prime = \dfrac{1}{4} \cdot 4 x^3 = \color{#99CC00}{x^3}$
Dritte Funktion: $F(x)= \dfrac{2}{3}x^3$
$\implies ~ f(x) = \left(\dfrac{2}{3}x^3\right)^\prime = \dfrac{2}{3} \cdot 3 x^2 = \color{#99CC00}{2x^2}$
Vierte Funktion: $F(x)=x^3$
$\implies ~ f(x) = \left(x^3\right)^\prime = \color{#99CC00}{3x^2}$
-
Stelle eine Stammfunktion auf.
TippsEine Stammfunktion von $f(x)=x^5$ wird gebildet, indem der Exponent um $1$ erhöht wird. Die Potenz lautet dann also $x^6$.
Um beim Ableiten wieder auf den Vorfaktor $1$ zu kommen, muss mit $\frac{1}{6}$ multipliziert werden. Eine Stammfunktion von $f$ lautet also:$F(x) = \dfrac{1}{6}x^6$
Beispiel:
$f(x)=36x^5+16x^3$
$F(x)=\left(36 \cdot \dfrac{1}{6}\right)x^6 + \left(16 \cdot \dfrac{1}{4}\right) x^4 = 6 x^6 + 4x^4$
LösungEine Stammfunktion $F$ ist so definiert, dass ihre Ableitung gleich $f$ ist:
$F^\prime(x)=f(x)$
Beim Bilden der Stammfunktion erhöhen wir den Exponenten der jeweiligen Potenz um $1$ und dividieren den Vorfaktor durch diesen erhöhten Exponenten. Die Potenzregel lautet also:
$f(x) = a \cdot x^n \quad \implies \quad {F(x) = \dfrac{a}{n+1}x^{n+1} + c \quad (c \in \mathbb{R})}$
Die Integrationskonstante $c$ kann eine beliebige reelle Zahl sein. In unseren Beispielen wurde $c=0$ gewählt.
Wird bei $f(x)$ eine reelle Zahl in der Funktion addiert, musst du bei der Stammfunktion ein $x$ anhängen.
Konstante Terme in $f$ werden mit der Variablen $x$ multipliziert, denn es gilt:
$x^0 = 1$
Die Lösung der Aufgabe lautet:
$f(x)=4x^3+6x^2+2$
$\implies F(x) = {4 \cdot \dfrac{1}{4}x^4 + 6 \cdot \dfrac{1}{3}x^3 +2x} = {x^4+2x^3+2x}$
$f(x)=15x^4+8x^3+9x^2$
$\implies F(x) = {15 \cdot \dfrac{1}{5}x^5 + 8 \cdot \dfrac{1}{4}x^4 + 9 \cdot \dfrac{1}{3}x^3} = {3x^5+2x^4+3x^3}$
$f(x)=45x^8-84x^6-51x^2$
$\implies F(x) = {45 \cdot \dfrac{1}{9}x^9 - 84 \cdot \dfrac{1}{7}x^7 - 51\cdot \dfrac{1}{3}x^3} = {5x^9-12x^7-17x^3}$
9.966
sofaheld-Level
6.600
vorgefertigte
Vokabeln
7.801
Lernvideos
37.162
Übungen
32.630
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Schulstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung


 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?