Integralfunktion – Definition

Integralfunktion – Definition Übung

• Gib an, ob die Aussagen über die Integralfunktion richtig sind.

  Tipps

  Die Integralfunktion $I_a(x)$ einer Funktion $f$ zur unteren Grenze $a$ entspricht einem bestimmten Integral, nur dass die obere Grenze kein fester Wert, sondern die Variable $x$ ist.

  Es gilt:

  $\int\limits_{a}^{a} f(x) \text{d}x = 0$

  Lösung

  Die Integralfunktion $I_a(x)$ einer Funktion $f$ zur unteren Grenze $a$ entspricht einem bestimmten Integral, nur dass die obere Grenze kein fester Wert, sondern die Variable $x$ ist. Wir schreiben:

  $I_a(x)=\displaystyle \int\limits_{a}^{x} f(t) ~\text{d}t$

  Dabei ist es wichtig, dass wir die abhängige Variable der Funktion $f$ nicht mit $x$ benennen, da das $x$ als obere Grenze verwendet wird.

  'Für die Integralfunktion gilt: $I_a(x)= \int\limits_{a}^{x} f(x) ~\text{d}x$.' – Falsch.

  'Anschaulich stellt die Integralfunktion die Flächenbilanz zwischen den beiden Grenzen dar.' – Richtig.

  Wir können die Integralfunktion konkret bestimmen, wenn wir die Funktion $f$ als Integrand und die untere Grenze $a$ gegeben haben. Dazu verwenden wir den Hauptsatz der Differential- und Integralrechnung:

  $\displaystyle I_a(x)= \int\limits_{a}^{x} f(t) ~\text{d}t = F(x) - F(a)$

  'Um die Integralfunktion konkret zu bestimmen, verwenden wir die Ableitungsregeln.' – Falsch, wir verwenden die Integrationsregeln.

  Wir setzen dann die obere und untere Grenze in eine gefundene Stammfunktion ein, und erhalten als Ergebnis einen Funktionsterm, so wie wir ihn gewohnt sind.

  'Eine Integralfunktion von $f$ ist immer auch eine Stammfunktion von $f$.' – Richtig.
  Allerdings handelt es sich um eine spezielle Stammfunktion: Denn sie hat bei der unteren Grenze $a$ eine Nullstelle, da der Funktionsterm durch $F(x)-F(a)$ gebildet wird. Wenn wir also für $x=a$ einsetzen, ergibt sich der Funktionswert Null. Es gilt: $\int\limits_{a}^{a} f(x) ~\text{d}x = 0$.

  'Die Integralfunktion hat bei der unteren Grenze $a$ eine Nullstelle.' – Richtig.

  Wir betrachten noch ein Beispiel:

  Wir betrachten die Funktion $f(x)=2x$. Für die Integralfunktion $I_a(x)$ wählen wir dann jedoch die abhängige Variable $t$ und schreiben:
  $\displaystyle I_a(x)= \int\limits_{a}^{x} f(t) ~\text{d}t = \int\limits_{a}^{x} 2t ~\text{d}t $
  Wählen wir als untere Grenze $a=0$, so ergibt sich:
  $\displaystyle I_0(x)= \int\limits_{0}^{x} 2t ~\text{d}t = \Big[t^2\Big]_{0}^{x} = x^2-0^2 = x^2 $
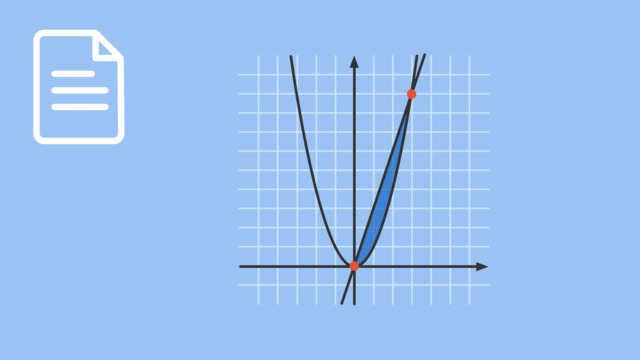
  Wir können also beispielsweise für $x=3$ die Flächenbilanz zwischen $0$ und $3$ unter dem Funktionsgraphen von $f(t)=2t$ bestimmen. (siehe Abbildung)

• Berechne die Funktionswerte der Integralfunktion.

  Tipps

  Wir können die Integralfunktion konkret mit dem Hauptsatz der Differential- und Integralrechnung bestimmen:

  $\displaystyle I_a(x)= \int\limits_{a}^{x} f(t) ~\text{d}t = F(x) - F(a)$

  Anschaulich stellt die Integralfunktion die Flächenbilanz zwischen den beiden Grenzen dar, hier zum Beispiel zwischen $0$ und $3$.

  $\displaystyle \int 2t ~\text{d}t = t^2 + c = F(t)$

  Lösung

  Die Integralfunktion $I_a(x)$ einer Funktion $f$ zur unteren Grenze $a$ entspricht einem bestimmten Integral, nur dass die obere Grenze kein fester Wert, sondern die Variable $x$ ist. Wir schreiben allgemein:

  $\displaystyle I_a(x)= \int\limits_{a}^{x} f(t)~ \text{d}t$

  In unserem Beispiel lautet die Integralfunktion also:

  $\displaystyle I_0(x)= \int\limits_{0}^{x} 2t ~\text{d}t$

  Anschaulich stellt die Integralfunktion die Flächenbilanz zwischen den beiden Grenzen dar.

  Wir können die Integralfunktion konkret mit dem Hauptsatz der Differential- und Integralrechnung bestimmen:

  $\displaystyle I_a(x)= \int\limits_{a}^{x} f(t) ~\text{d}t = F(x) - F(a)$

  In unserem Beispiel wenden wir ihn wie folgt an:

  $ \displaystyle I_0(x)= \int\limits_{0}^{x} 2t ~\text{d}t = \Bigl[t^2\Bigr]_{0}^{x} = x^2-0^2 = x^2 $

  Wir können also beispielsweise für $x=1{,}5$ die Flächenbilanz zwischen $0$ und $1{,}5$ unter dem Funktionsgraphen von $f(t)=2t$ bestimmen. Dazu setzen wir in die gefundene Integralfunktion ein:
  $I_0(1{,}5) = 1{,}5^2 = 2{,}25$

  So ergeben sich auch die anderen Funktionswerte:

  • $I_0(2) = 2^2 = 4$
  • $I_0(3) = 3^2 = 9$
  • $I_0(5) = 5^2 = 25$

• Bestimme den Funktionsterm der Integralfunktionen $I_a(x)$.

  Tipps

  Setze zunächst $a$ und $f(t)$ in die Integralfunktion

  $\displaystyle I_a(x)= \int\limits_{a}^{x} f(t) ~\text{d}t$ ein.

  Beispiel: $a=3$ und $f(t)=4t^2$

  $\displaystyle I_3(x)= \int\limits_{3}^{x} 4t^2 ~\text{d}t = \Bigl[\frac{4}{3}t^3\Bigr]_{3}^{x} = \frac{4}{3}x^3-\frac{4}{3} \cdot 3^3 = \frac{4}{3}x^3-36$

  Lösung

  Wir können die Integralfunktion $I_a(x)= \int\limits_{a}^{x} f(t) ~\text{d}t$ mit dem Hauptsatz der Differential- und Integralrechnung bestimmen. Dazu setzen wir jeweils zuerst $a$ und $f(t)$ ein, und bestimmen dann das Integral:

  Beispiel 1: $a=1$ und $f(t)=2t^2$

  $\displaystyle I_1(x)= \int\limits_{1}^{x} 2t^2 ~\text{d}t = \bigg[\frac{2}{3}t^3\bigg]_{1}^{x} = \frac{2}{3}x^3-\frac{2}{3} \cdot 1^3 = \frac{2}{3}x^3-\frac{2}{3}$

  Beispiel 2: $a=3$ und $f(t)=t^3$

  $\displaystyle I_3(x)= \int\limits_{3}^{x} t^3 \text{d}t = \bigg[\frac{1}{4}t^4\bigg]_{3}^{x} = \frac{1}{4}x^4-\frac{1}{4} \cdot 3^4 = \frac{1}{4}x^4-\frac{81}{4}$

  Beispiel 3: $a=1$ und $f(t)=3t^2$

  $\displaystyle I_1(x)= \int\limits_{1}^{x} 3t^2 \text{d}t = \Bigl[ t^3\Bigr]_{1}^{x} = x^3-1^3 = x^3-1$

  Beispiel 4: $a=2$ und $f(t)=2t^3$

  $\displaystyle I_2(x)= \int\limits_{2}^{x} 2t^3 \text{d}t = \bigg[\frac{1}{2}t^4\bigg]_{2}^{x} = \frac{1}{2}x^4- \frac{1}{2}\cdot 2^4 = \frac{1}{2}x^4-8$

• Ermittle die Integralfunktion für unterschiedliche Werte von $a$.

  Tipps

  $f(t) = \sqrt t = t^{\frac{1}{2}}$

  Die Wurzel aus einer negativen Zahl kann nicht gezogen werden.

  Beispiel: $a=3$
  $I_3(x)= \int\limits_{3}^{x} \sqrt t ~\text{d}t = \Bigl[\frac{2}{3} \sqrt {t^3}\Bigr]_{3}^{x} = \frac{2}{3} \sqrt {x^3} - \frac{2}{3} \sqrt {3^3} = \frac{2}{3} \sqrt {x^3} - 2 \sqrt 3 $

  Lösung

  Um die Integralfunktion $I_a(x)= \int\limits_{a}^{x} \sqrt t ~\text{d}t$ zu bestimmen, setzen wir die gegebenen Werte für $a$ ein und bestimmen dann das Integral mit dem Hauptsatz der Differential- und Integralrechnung:

  $\displaystyle I_a(x)= \int\limits_{a}^{x} f(t) ~\text{d}t = F(x) - F(a)$

  Wir benötigen also die Stammfunktion der gegebenen Funktion $f(t) = \sqrt t$. Dazu schreiben wir sie als Potenz und berechnen die Stammfunktion mithilfe der Potenzregel:

  $\displaystyle f(t) = \sqrt t = t^{\frac{1}{2}} \quad \Rightarrow \quad F(t)= \frac{1}{\frac{1}{2} +1} t^{\frac{1}{2}+1} = \frac{1}{\frac{3}{2}} t^{\frac{3}{2}} = \frac{2}{3} \sqrt {t^3}$

  
  

  • $a=1$:

  $\displaystyle I_1(x)= \int\limits_{1}^{x} \sqrt t ~\text{d}t = \bigg[\frac{2}{3} \sqrt {t^3}\bigg]_{1}^{x} = \frac{2}{3} \sqrt {x^3} - \frac{2}{3} \sqrt {1^3} = \frac{2}{3} \sqrt {x^3} - \frac{2}{3}$

  • $a=0$:

  $ \displaystyle I_0(x)= \int\limits_{0}^{x} \sqrt t ~\text{d}t = \bigg[\frac{2}{3} \sqrt {t^3}\bigg]_{0}^{x} = \frac{2}{3} \sqrt {x^3} - \frac{2}{3} \sqrt {0^3} = \frac{2}{3} \sqrt {x^3}$

  • $a=2$:

  $\displaystyle I_2(x)= \int\limits_{2}^{x} \sqrt t ~\text{d}t = \bigg[\frac{2}{3} \sqrt {t^3}\bigg]_{2}^{x} = \frac{2}{3} \sqrt {x^3} - \frac{2}{3} \sqrt {2^3} = \frac{2}{3} \sqrt {x^3} - \frac{4}{3} \sqrt 2$

  • $a=-1$:

  $\displaystyle I_{-1}(x)= \int\limits_{-1}^{x} \sqrt t ~\text{d}t = \bigg[\frac{2}{3} \sqrt {t^3}\bigg]_{-1}^{x} = \frac{2}{3} \sqrt {x^3} - \frac{2}{3} \sqrt {(-1)^3} = \frac{2}{3} \sqrt {x^3} - \frac{2}{3} \sqrt {-1}$
  Hier müsste die Wurzel aus einer negativen Zahl gezogen werden. Dies ist nicht möglich. Daher ist $I_{-1}(x)$ nicht definiert.

  • $a=4$:

  $\displaystyle I_4(x)= \int\limits_{4}^{x} \sqrt t ~\text{d}t = \bigg[\frac{2}{3} \sqrt {t^3}\bigg]_{4}^{x} = \frac{2}{3} \sqrt {x^3} - \frac{2}{3} \sqrt {4^3} = \frac{2}{3} \sqrt {x^3} - \frac{16}{3}$

• Stelle die markierte Fläche als Integral dar.

  Tipps

  In den Abbildungen können wir direkt die Integralgrenzen ablesen. Außerdem können wir die Funktionsart (linear, quadratisch, trigonometrisch) identifizieren und die Integrale so zuordnen.

  $A= \displaystyle \int\limits_{0}^{2} t^2+1 ~\text{d}t$

  Lösung

  Wir wissen nun, dass die Integralfunktion $I_a(x)$ einer Funktion $f$ zur unteren Grenze $a$ einem bestimmten Integral entspricht. Bei diesem bestimmten Integral ist wichtig, dass die obere Grenze kein fester Wert, sondern die Variable $x$ ist. Anschaulich stellt die Integralfunktion die Flächenbilanz zwischen den beiden Grenzen dar.

  Genauso können wir ein bestimmtes Integral $\int\limits_a^b f(x)~\text{d}x$ als Flächenbilanz zwischen dem Funktionsgraphen und der $x$-Achse interpretieren. Die Integralgrenzen $a$ und $b$ beschreiben dabei die Geraden $x = a$ und $x = b$, welche die Fläche begrenzen.

  In den Abbildungen können wir also immer direkt die Integralgrenzen ablesen. Außerdem können wir die Funktionsart (linear, quadratisch, trigonometrisch) identifizieren und die Integrale so zuordnen:

  • Abbildung 1: Grenzen $1$ und $3$, quadratische Funktion $\quad \Rightarrow \quad \int\limits_{1}^{3} t^2 ~\text{d}t$
  • Abbildung 2: Grenzen $1$ und $4$, lineare Funktion $\quad \Rightarrow \quad \int\limits_{1}^{4} t+1 ~\text{d}t$
  • Abbildung 3: Grenzen $1$ und $4$, quadratische Funktion $\quad \Rightarrow \quad \int\limits_{1}^{4} (t-2)^2+1 ~\text{d}t$
  • Abbildung 4: Grenzen $2$ und $5$, trigonometrische Funktion $\quad \Rightarrow \quad \int\limits_{2}^{5} 0,5 \cos (-x+3)+1 ~\text{d}t$

• Überprüfe die Zusammenhänge zwischen Integralfunktion, Funktion und Ableitungen.

  Tipps

  Eine Integralfunktion von $f$ ist immer auch eine Stammfunktion von $f$.

  $I_a(a) = F(a) - F(a)= 0$

  Das bedeutet, die untere Grenze $a$ einer Integralfunktion ist gleichzeitig auch immer eine Nullstelle der Integralfunktion.

  Lösung

  Die Integralfunktion $I_a(x)$ einer Funktion $f$ zur unteren Grenze $a$ entspricht einem bestimmten Integral, nur dass die obere Grenze kein fester Wert, sondern die Variable $x$ ist:

  $\displaystyle I_a(x)= \int\limits_{a}^{x} f(t) ~\text{d}t$

  Dabei gilt:

  • Aussage 1: Eine Integralfunktion von $f$ ist immer auch eine Stammfunktion von $f$.
  • Aussage 2: Die Integralfunktion hat bei der unteren Grenze $a$ eine Nullstelle.

  Wir betrachten dazu ein Beispiel: $f(x)=2x$. Für die Integralfunktion $I_a(x)$ wählen wir die Variable $t$ für $f(t)=2t$ und schreiben:

  $\displaystyle I_a(x)= \int\limits_{a}^{x} f(t) ~\text{d}t = \int\limits_{a}^{x} 2t \text{d}t = \Bigl[t^2\Bigr]_{a}^{x} = x^2-a^2 $

  Wir überprüfen nun die Aussagen:

  • $I_3(3)=0$ $\quad$ richtig wegen Aussage 1, im Beispiel gilt: $I_3(3)=3^2-3^2=0$
  • $I_3(0)=0$ $\quad$ falsch wegen Aussage 1, im Beispiel gilt: $I_3(0)=0^2-3^2=-9$
  • $I''_0(x)=f'(x)$ $\quad$ richtig wegen Aussage 2, im Beispiel gilt: $I''_0(x)=(x^2)'' = (2x)' = 2 = f'(x)$
  • $I''_3(x)=f'(x)+3x$ $\quad$ falsch wegen Aussage 2, im Beispiel gilt: $I''_0(x)=(x^2)'' = (2x)' = 2 = f'(x)$
  • $I'_0(x)=0$ $\quad$ falsch wegen Aussage 2, im Beispiel gilt: $I'_0(x)=(x^2)' = 2x$
  • $I'_1(x)=f'(x)$ $\quad$ falsch wegen Aussage 2, im Beispiel gilt: $I'_1(x)=(x^2-1)' = 2x = f(x)$