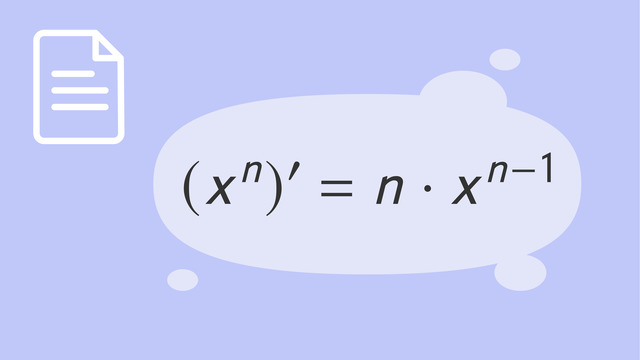Potenzregel bei Ableitungen
Du möchtest schneller & einfacher lernen?
Grundlagen zum Thema Potenzregel bei Ableitungen
Nach dem Schauen dieses Videos wirst du in der Lage sein, Potenzfunktionen mit Hilfe der Potenzregel abzuleiten.
In diesem Video lernst du, dass du den Exponenten einer Potenzfunktion als Faktor nach vorne ziehen und anschließend um 1 verringern musst, um sie abzuleiten.
Das Video beinhaltet Schlüsselbegriffe, Bezeichnungen und Fachbegriffe wie Potenzregel, Ableitung, Potenzfunktion und Exponent.
Bevor du dieses Video schaust, solltest du bereits wissen, was eine Ableitung ist.
Nach diesem Video wirst du darauf vorbereitet sein, die Faktor- und Summenregel bei Ableitungen zu lernen.
Transkript Potenzregel bei Ableitungen
Warum ist die Welt so, wie sie ist?
Wäre es nicht schön, alle Hintergründe und Zusammenhänge zu kennen?
Manchmal wünscht du dir aber vielleicht auch einfach, dass dir jemand sagt, was zu tun ist.
Das Leben ist ja so schon kompliziert genug, nicht wahr?
Zum Beispiel wenn im Matheunterricht das Thema „Ableitungen“ auf dem Programm steht.
Gut, dass es da die „Potenzregel“ gibt.
Die Potenzregel ist ganz einfach zu merken und sagt uns was zu tun ist, wenn wir die Ableitung einer Potenzfunktion bestimmen wollen.
Schnappen wir uns also mal so eine Potenzfunktion! Zum Beispiel „f von x gleich x hoch drei“.
Die Ableitungsfunktion „f-Strich von x“ bilden wir ganz einfach, indem wir den Exponenten, also die Hochzahl, als Faktor nach vorne ziehen, und den Exponenten dann um eins verringern.
„drei x hoch zwei“ ist dann unsere Ableitungsfunktion.
Okay, das ist echt kein Aufwand.
Wir müssen also – Erstens: Den Exponenten der Potenz als Faktor vor die Potenz schreiben.
Und zweitens: Den Exponenten um eins verringern.
Die Ableitung von „x hoch sechs“ lautet also?
Richtig, „sechs x hoch fünf“.
Wenn wir eine Ableitungsfunktion einer bestimmten Funktion berechnen wollen, müssen wir also nicht immer den Differentialquotienten bemühen.
Den Stress geben wir uns jetzt nicht mehr.
Stattdessen können wir Potenzfunktionen einfach nach dem hier gezeigten Muster ableiten. Komplett entspannt!
Schauen wir uns das nochmal in einer Tabelle an: Was erhalten wir denn, wenn wir x ableiten?
Nun ja, x können wir auch als „x hoch eins“ schreiben.
Wenn wir den Exponenten nach vorne ziehen und dann um eins verringern, erhalten wir als Ableitung „eins mal x hoch null“.
„X hoch null“ ist eins“.
Daher ist die Ableitung von x einfach gleich eins.
„x hoch zwei“ abgeleitet, wird „2 x hoch eins“, also einfach „zwei x“, die Ableitung von „x hoch drei“ ist „drei x hoch zwei“, und so weiter.
Allgemein formuliert lautet die Potenzregel: Die Ableitung der Funktion „x hoch n“ ist „n mal x hoch n-minus-eins“.
Mit Hilfe dieser Regel können wir auch die Steigung einer Potenzfunktion an einer bestimmten Stelle kinderleicht herausfinden.
Wir erinnern uns: Die Ableitung gibt ja die Steigung einer Funktion an jeder beliebigen Stelle an.
Wollen wir zum Beispiel wissen, welche Steigung die Funktion „x hoch drei“ an der Stelle „minus-vier“ hat, bilden wir die Ableitungsfunktion mit der Potenzregel.
Dann müssen wir dort nur noch minus-vier einsetzen und haben unser Ergebnis: Die Steigung an der betrachteten Stelle beträgt achtundvierzig.
Wir fassen noch einmal auf einen Blick zusammen.
Mit der Potenzregel können wir Potenzfunktionen ganz einfach und ohne große Rechnerei ableiten.
Im konkreten Fall müssen wir dafür nur: Den Exponenten als Faktor nach vorne ziehen, und um eins verringern.
So gelingt das Ableiten im Handumdrehen!
Und wir haben mehr Zeit, um über die ganz großen Fragen des Lebens zu philosophieren: Wie groß ist eigentlich das Universum?
Wie kann es sein, dass überhaupt etwas existiert? Und warum?
Potenzregel bei Ableitungen Übung
-
Gib die Potenzregel bei Ableitungen an.
TippsBeispiel:
$f(x) = x^4$
$f^\prime(x) = 4x^3$
Differentialquotient:
$\lim\limits_{h \to 0} \dfrac{f(x_0 + h) - f(x_0)}{h}$
Gibt die Steigung einer Funktion bei $x_0$ an.
LösungWir können die Steigung eines Funktionsgraphen bereits mithilfe des Differentialquotienten bestimmen:
$\lim\limits_{h \to 0} \dfrac{f(x_0 + h) - f(x_0)}{h}$ gibt die Steigung von $f(x)$ bei $x_0$ an.
Damit wir nicht jedes mal einen Grenzwert bilden müssen, können wir die Potenzregel zum Ableiten verwenden.Potenzregel:
$f(x) = x^n \quad \rightarrow \quad f^\prime(x) = n \cdot x^{n-1}$
Wir bilden die Ableitung, indem wir den Exponenten als Faktor nach vorne ziehen und den Exponenten dann um 1 verringern.
Beispiel:
$f(x) = x^2$
$f^\prime(x) = 2 \cdot x^{2-1} = \mathbf{2x}$ -
Berechne die Steigung des Graphen.
TippsZunächst musst du die Ableitung der Funktion mit der Potenzregel bestimmen.
Beispiel:
LösungUm die Steigung eines Funktionsgraphen an einem bestimmten Punkt zu bestimmen, können wir den zugehörigen $x$-Wert in den Term der Ableitung einsetzen. Wir erhalten die gesuchte Steigung.
Beispiel: $f(x) = x^7 \qquad x_0 = -0,8$
Wir bestimmen zunächst die Ableitung $f^\prime(x)$ mit der Potenzregel:
$f^\prime(x) = 7 \cdot x^{7-1} = 7x^6$
Die Steigung des Graphen von $f$ entspricht dem Wert der Ableitung. Um die Steigung an der Stelle $x_0 = -0,8$ zu erhalten, setzen wir diesen Wert für $x$ in den Term der Ableitung ein:
$f^\prime(-0,8) = 7 \cdot (-0,8)^6 = 7 \cdot 0,262144 = 1,8350.. \approx 1,8$
$\Rightarrow$ Der Graph von $f(x)$ hat bei $x_0 = -0,8$ die Steigung $1,8$.
-
Bestimme die Steigung an der Stelle $x_0$.
TippsPotenzregel:
$f(x) = x^n$
$f^\prime(x) = n \cdot x^{n-1}$Steigung von $f(x) = x^2$ bei $x_0 = 2$:
$f^\prime(x) = 2x$
$f^\prime(2) = 2 \cdot 2 = 4$LösungUm die Steigung eines Funktionsgraphen an einem bestimmten Punkt zu bestimmen, können wir den zugehörigen $x$-Wert in den Term der Ableitung einsetzen. Wir erhalten die gesuchte Steigung.
Beispiel: $f(x) = x^8 \qquad x_0 = -1$
Wir bestimmen zunächst die Ableitung $f^\prime(x)$ mit der Potenzregel:
$f^\prime(x) = 8 \cdot x^{8-1} = 8x^7$
Die Steigung des Graphen von $f$ entspricht dem Wert der Ableitung. Um die Steigung an der Stelle $x_0 = -1$ zu erhalten, setzen wir diesen Wert für $x$ in den Term der Ableitung ein:
$f^\prime(-1) = 8 \cdot (-1)^7 = 8 \cdot (-1) = -8$
Hinweis:
Der Wert $x_0 = -1$ muss bei der Berechnung von $f^\prime(-1)$ in Klammern gesetzt werden, da sich bei $-1^2$ der Exponent nur auf die Zahl $1$, nicht aber auf das Vorzeichen bezieht. -
Ermittle die Ableitung mithilfe der Potenzregel.
TippsPotenzregel:
- Schreibe den Exponenten als Faktor vor die Potenz.
- Verringere den Exponenten um 1.
Die Potenzregel gilt auch für Exponenten, die keine natürlichen Zahlen sind.
Beispiel:
$f(x) = x^{-2}$
$f^\prime(x) = -2x^{-3}$LösungWir können die Potenzregel anwenden, um die Ableitung einer beliebigen Funktion der Form $x^n$ zu bestimmen. Es gilt:
$f^\prime(x) = n \cdot x^{n-1}$
Die Regel gilt auch dann, wenn $n$ eine negative Zahl, ein Bruch oder eine Dezimalzahl ist.
Beispiel 1: $f(x) = x^{137}$
$\Rightarrow \quad f^\prime(x) = 137 \cdot x^{137 - 1} = 137x^{136}$Beispiel 2: $f(x) = x^{2,5}$
$\Rightarrow \quad f^\prime(x) = 2,5 \cdot x^{2,5-1} = 2,5x^{1,5}$Beispiel 3: $f(x) = x^{-5}$
$\Rightarrow \quad f^\prime(x) = -5 \cdot x^{-5-1} = -5x^{-6}$Beispiel 4: $f(x) = x^{-1,5}$
$\Rightarrow \quad f^\prime(x) = -1,5 \cdot x^{-1,5-1} = -1,5x^{-2,5}$Beispiel 5: $f(x) = x^{0,5}$
$\Rightarrow \quad f^\prime(x) = 0,5 \cdot x^{0,5-1} = 0,5x^{-0,5}$ -
Beschreibe die Bedeutung der Ableitung einer Funktion.
TippsDer Anstieg eines Funktionsgraphen wird auch momentane oder lokale Änderungsrate genannt.
Wir können die Ableitung eines Funktionsterm zum Beispiel ermitteln, indem wir den Grenzwert des Differenzenquotienten, den sogenannten Differentialquotienten, bestimmen.
LösungWenn wir die Steigung einer Funktion bestimmen wollen, dann können wir dazu die Ableitung der Funktion nutzen. Diese beschreibt den Anstieg des Funktionsgraphen für beliebige $x$-Werte.
Der Anstieg entspricht der Steigung einer Tangente an den Graphen und wird auch als lokale oder momentane Änderungsrate der Funktion bezeichnet.Die folgenden Aussagen sind daher korrekt:
- Die Ableitung gibt die Steigung einer Tangente an den Graphen an.
- Die Ableitung beschreibt die lokale Änderungsrate einer Funktion.
Die folgenden Aussagen sind nicht korrekt:
- Die Potenzregel ist die einzige Möglichkeit die Ableitung einer Funktion zu ermitteln.
- Nur Potenzfunktionen haben eine Ableitung.
-
Entscheide, ob die Potenzregel richtig angewendet wurde.
TippsÜberprüfe, ob der Faktor vor $x$ in der Ableitung dem Exponenten der Funktion entspricht.
Der Exponent wird beim Ableiten mit der Potenzregel stets um 1 verringert.
LösungZur korrekten Ableitung einer Funktion der Form $x^n$ mit der Potenzregel schreiben wir den Exponenten $n$ als Faktor vor $x$ und verringern die Zahl im Exponenten um 1. Dabei ist es nicht relevant, ob der Exponent eine natürliche Zahl, eine negative Zahl oder ein Bruch ist.
Die Regel lautet:
$f(x)=x^n \quad \rightarrow \quad f^\prime(x) = n \cdot x^{n-1}$Wir überprüfen, ob die beiden Schritte richtig angewendet wurden:
Beispiel 1: $f(x) = x^{\frac{2}{3}}$ mit $f^\prime(x) = \frac{2}{3} \cdot x^{\frac{1}{3}}$
Hier ist $n = \frac{2}{3}$ und $n - 1 = \frac{2}{3} - 1 = -\frac{1}{3}$.
$\Rightarrow \quad f^\prime(x) = \frac{2}{3} \cdot x^{-\frac{1}{3}}$
Der Faktor ist korrekt, aber der Exponent stimmt nicht.Beispiel 2: $f(x) = x^{-3}$ mit $f^\prime(x) = -3 \cdot x^{-4}$
Hier ist $n = -3$ und $n - 1 = -3 - 1 = -4$.
$\Rightarrow \quad f^\prime(x) = -3 \cdot x^{-4}$
Der Faktor und der Exponent sind korrekt.Beispiel 3: $f(x) = x^{0,2}$ mit $f^\prime(x) = 0,2 \cdot x^{-0,2}$
Hier ist $n = 0,2$ und $n - 1 = 0,2 - 1 = -0,8$.
$\Rightarrow \quad f^\prime(x) = 0,2 \cdot x^{-0,8}$
Der Faktor ist korrekt, aber der Exponent stimmt nicht.Beispiel 4: $f(x) = x^{-9}$ mit $f^\prime(x) = 9 \cdot x^{-10}$
Hier ist $n = -9$ und $n - 1 = -9 - 1 = -10$.
$\Rightarrow \quad f^\prime(x) = -9 \cdot x^{-10}$
Der Exponent ist korrekt, aber der Faktor stimmt nicht.Beispiel 5: $f(x) = x^{-1,7}$ mit $f^\prime(x) = -1,7 \cdot x^{-2,7}$
Hier ist $n = -1,7$ und $n - 1 = -1,7 - 1 = -2,7$.
$\Rightarrow \quad f^\prime(x) = -1,7 \cdot x^{-2,7}$
Der Faktor und der Exponent sind korrekt.Beispiel 6: $f(x) = x^{\frac{2}{7}}$ mit $f^\prime(x) = -\frac{2}{7} \cdot x^{-\frac{5}{7}}$
Hier ist $n = \frac{2}{7}$ und $n - 1 = \frac{2}{7} - 1 = -\frac{5}{7}$.
$\Rightarrow \quad f^\prime(x) = \frac{2}{7} \cdot x^{-\frac{5}{7}}$
Der Exponent ist korrekt, aber der Faktor stimmt nicht.
4.200
sofaheld-Level
6.572
vorgefertigte
Vokabeln
8.917
Lernvideos
38.941
Übungen
35.045
Arbeitsblätter
24h
Hilfe von Lehrer*
innen
Inhalte für alle Fächer und Schulstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Primzahlen
- Geometrische Lagebeziehungen
- Rechteck
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Quadrat
- Division
- Raute
- Parallelogramm
- Was ist eine Viertelstunde
- Prisma
- Mitternachtsformel
- Grundrechenarten Begriffe
- Dreiecksarten
- Quader
- Satz des Pythagoras
- Dreieck Grundschule
- Kreis
- Standardabweichung
- Flächeninhalt
- Volumen Kugel
- Zahlen in Worten schreiben
- Meter
- Orthogonalität
- Schriftlich multiplizieren
- Brüche multiplizieren
- Potenzgesetze
- Distributivgesetz
- Flächeninhalt Dreieck
- Rationale Zahlen
- Volumen berechnen
- Brüche addieren
- Kongruenz
- Exponentialfunktion
- Scheitelpunktform
- Logarithmus
- Skalarprodukt
- Primfaktorzerlegung
- Quadratische Ergänzung
- Zinseszins
- Geradengleichung aus zwei Punkten bestimmen
- Sinusfunktion
- Natürliche Zahlen
- Brüche dividieren
- Sinus
