Brüche addieren und subtrahieren
Hauptnenner, Nenner gleich machen, nennergleich machen, kgV
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
Was ist ein Bruch?
Was genau verstehen wir unter einem Bruch? Stell dir vor, du möchtest einen Apfel in fünf gleich große Stücke teilen. Jedes dieser Stücke ist dann ein Fünftel.
Wenn du nun deiner Schwester drei Stücke gibst und für dich zwei behältst, bekommt deine Schwester $3$ Fünftel und du $2$ Fünftel des Apfels.
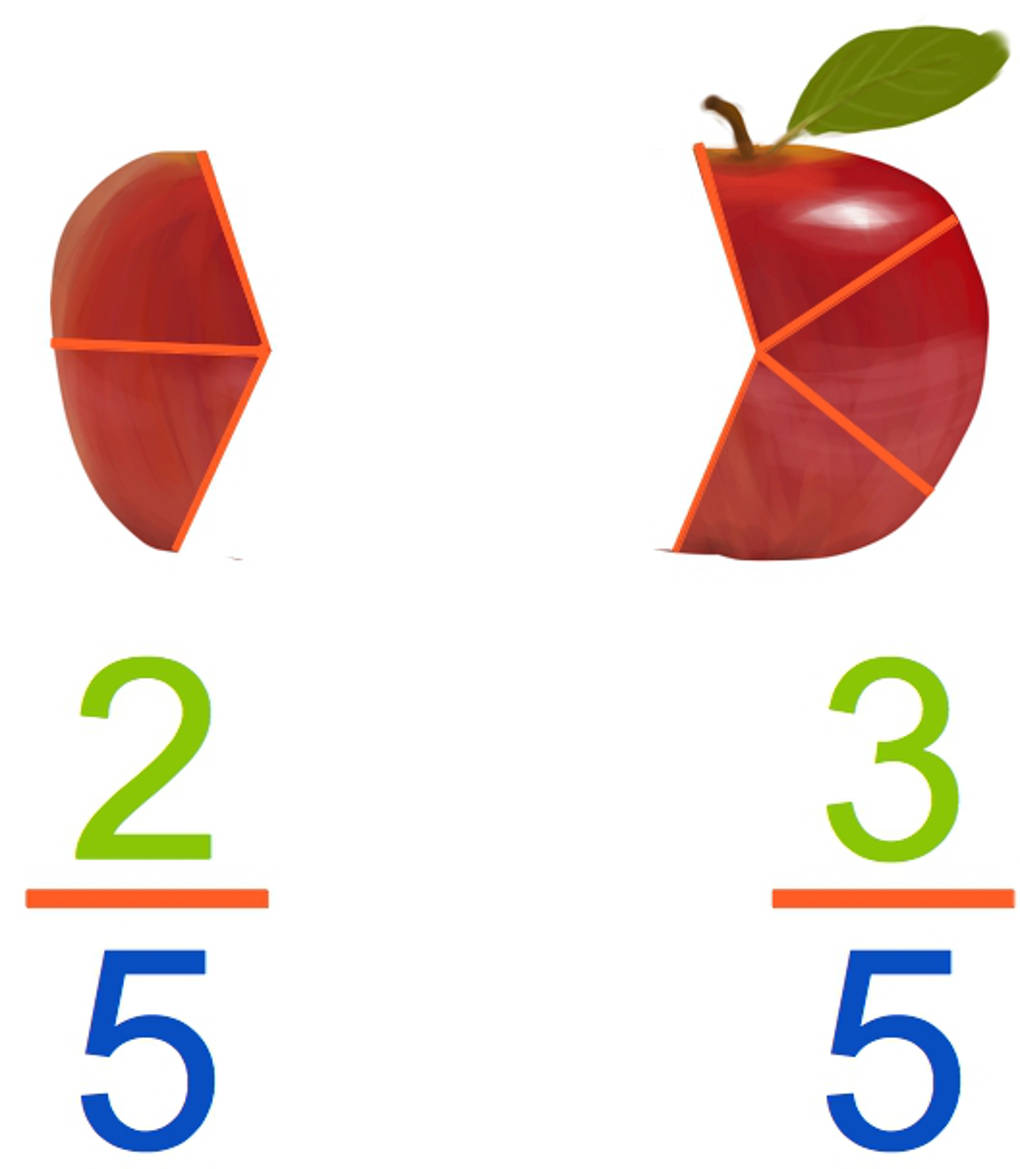
Alle Brüche sind gleich aufgebaut:
- Sie haben einen Strich, den Bruchstrich. Dieser steht für das Divisionszeichen. Es wird die obere durch die untere Zahl dividiert.
- Die Zahl unter dem Bruchstrich heißt Nenner. Dieser benennt den Bruch (hier: Fünftel). Der Nenner zeigt somit an, in wie viele Teile ein Ganzes geteilt wird.
- Die Zahl über dem Bruchstrich heißt Zähler. Er gibt die Anzahl der Teile des Ganzen an. Hier sind dies einmal $2$ und einmal $3$.
Was sind gleichnamige Brüche?
Brüche mit gleichem Nenner werden als gleichnamig bezeichnet. Die beiden Brüche, welche beim Teilen des Apfels entstehen, sind gleichnamig. Beide Brüche zeigen Fünftel an.
Nun wollen wir untersuchen, wie wir Brüche addieren können.
Wie werden zwei Brüche addiert?
Addition von gleichnamigen Brüchen
Du kannst Brüche nur addieren, wenn sie den gleichen Nenner haben, also gleichnamig sind. Was ist zu tun?
- Du addierst die Zähler und
- behältst den Nenner bei.
Lass uns dies einmal an einem Beispiel üben:
$\frac38+\frac28=\frac{3+2}8=\frac58$.
Was tun wir aber, wenn die Brüche nicht gleichnamig sind?
Addition von Brüchen, die nicht gleichnamig sind
Aber auch Brüche, die nicht gleichnamig sind, kannst du addieren. Hierfür musst du die Brüche erst einmal gleichnamig machen, indem du kürzt oder erweiterst. Wir wollen $\frac13+\frac15$ berechnen.
Bringe die beiden Brüche zuerst auf einen gemeinsamen Nenner. Das kleinste gemeinsame Vielfache der beiden Brüche ist $15$.
$\frac13+\frac15=\frac{1\cdot 5}{3\cdot 5}+\frac{1\cdot 3}{5\cdot 3}=\frac{5}{15}+\frac{3}{15}$
Nun kannst du die Zähler addieren und den Nenner beibehalten:
$\frac13+\frac15=\frac{5}{15}+\frac{3}{15}=\frac{5+3}{15}=\frac{8}{15}$.
Wie werden Brüche subtrahiert?
Ebenso wie beim Addieren von gleichnamigen Brüchen gehst du beim Subtrahieren vor. Du subtrahierst zwei Brüche, indem du
- die Zähler subtrahierst und
- den Nenner beibehältst.
Das üben wir auch gleich einmal:
$\frac78-\frac48=\frac{7-4}{8}=\frac38$.
Subtraktion von Brüchen, die nicht gleichnamig sind
Wenn die Brüche nicht gleichnamig sind, musst du sie auch beim Subtrahieren durch Erweitern oder Kürzen gleichnamig machen. Hierfür schauen wir uns wieder ein Beispiel an: $\frac13-\frac15$.
Bringe die beiden Brüche zunächst auf den gemeinsamen Nenner $15$:
$\frac13-\frac15=\frac{1\cdot 5}{3\cdot 5}-\frac{1\cdot 3}{5\cdot 3}=\frac{5}{15}-\frac{3}{15}$.
Nun kannst du die Differenz der Zähler bilden und den Nenner beibehalten:
$\frac13-\frac15=\frac{5}{15}-\frac{3}{15}=\frac{5-3}{15}=\frac{2}{15}$.
Beispiele
Pauls Geburtstagskuchen
Paul hatte Geburtstag. Es gab seinen Lieblingskuchen, einen Erdbeerkuchen. Diesen hat Paul in zwölf gleich große Stücke, also Zwölftel, geteilt. Am Abend sind noch fünf Zwölftel übrig. Er möchte seiner besten Freundin zwei Zwölftel mit nach Hause geben. Wie viel Kuchen bleibt übrig? Ja, hier muss Paul zwei gleichnamige Brüche subtrahieren:
$\frac{5}{12}-\frac{2}{12}=\frac{5-2}{12}=\frac{3}{12}$.
Ein Zwölftel ist genau ein Stück Kuchen. Dann kannst du auch von den verbleibenden fünf Stück Kuchen zwei abziehen und erhältst so drei Stück Kuchen. Das sind $\frac{3}{12}$ des Kuchens.
Luke trainiert für einen Laufwettbewerb
Luke möchte an einem Laufwettbewerb teilnehmen. Er hat zehn Tage davor begonnen zu trainieren. Drei Tage sind schon vergangen, sieben Tage hat er noch vor sich. Das sind $7$ Zehntel seiner gesamten Trainingszeit. Die nächsten $5$ Tage möchte er Ausdauerläufe trainieren. Fünf Tage sind genau die Hälfte der $10$ Tage. Welcher Teil der gesamten Trainingszeit bleibt ihm nach den $5$ Tagen noch?
$\frac{7}{10}-\frac12$
Zuerst muss er die Brüche gleichnamig machen. Siehst du den gemeinsamen Nenner? Der ist $10$. Also muss der rechte der beiden Brüche mit $5$ erweitert werden:
$\frac{7}{10}-\frac12=\frac{7}{10}-\frac{1\cdot 5}{2\cdot 5}=\frac{7}{10}-\frac{5}{10}$.
Nun subtrahiert er die Zähler und behält die Nenner bei:
$\frac{7}{10}-\frac12=\frac{7}{10}-\frac{5}{10}=\frac{7-5}{10}=\frac{2}{10}$.
Es bleiben ihm also noch zwei Zehntel der Gesamtzeit zu weiteren Trainingseinheiten.
Addition und Subtraktion von Brüchen
Paul und Luke üben gemeinsam das Addieren und Subtrahieren von Brüchen. Gemeinsam werden sie das schon schaffen: $\frac12-\frac13+\frac1{12}-\frac14$.
- Zuerst subtrahieren sie die ersten beiden Brüche: $\frac12-\frac13=\frac36-\frac26=\frac16$.
- Nun addieren sie: $\frac16+\frac1{12}=\frac2{12}+\frac1{12}=\frac3{12}$.
- Diesen Bruch können sie kürzen: $\frac3{12}=\frac14$.
- Nun müssen sie noch einmal subtrahieren: $\frac14-\frac14=0$.
Nun sind sie fertig und können endlich noch ein Stück Kuchen essen.
Alle Videos zum Thema
Videos zum Thema
Brüche addieren und subtrahieren (6 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Brüche addieren und subtrahieren (6 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung








 Brüche gleichnamig machen
Brüche gleichnamig machen
 Addition von Brüchen
Addition von Brüchen
 Brüche addieren
Brüche addieren
 Brüche addieren – Übungen
Brüche addieren – Übungen
 Brüche subtrahieren – Überblick
Brüche subtrahieren – Überblick
 Brüche subtrahieren – ausführliche Erklärung
Brüche subtrahieren – ausführliche Erklärung









