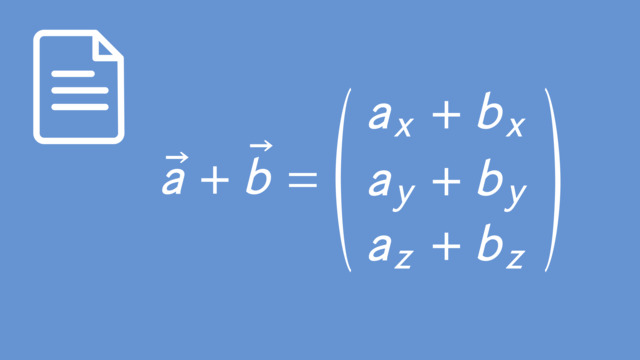Vektorrechnung

Über 1,6 Millionen Schüler*innen nutzen sofatutor!

93%
haben mit sofatutor ihre Noten in mindestens einem Fach verbessert
94%
verstehen den Schulstoff mit sofatutor besser
92%
können sich mit sofatutor besser auf Schularbeiten vorbereiten

Lerntext zum Thema Vektorrechnung

Was ist Vektorrechnung?

Die Vektorrechnung ist ein Teilbereich der Mathematik, der sich mit sogenannten Vektoren beschäftigt. Mit Hilfe von Vektoren kannst du Richtungen und Größen wie Geschwindigkeit, Kraft oder Verschiebungen mathematisch exakt darstellen.

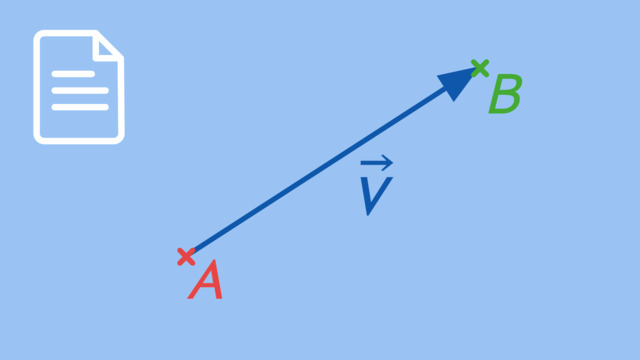
Was sind Vektoren?

Ein Vektor ist eine Größe, die sowohl eine Richtung als auch eine Länge besitzt. Stell dir vor, du gehst $5$ Schritte geradeaus und anschließend $3$ Schritte nach links. Genau diese Kombination aus Bewegungen in verschiedene Richtungen kann als Vektor dargestellt werden.

Dreidimensionale Vektoren schreibst du in der Mathematik meist so auf:

$$ \vec{v} = \begin{pmatrix} v_x \\ v_y \\ v_z \end{pmatrix} $$

Dabei gibt $v_x$, $v_y$ und $v_z$ die jeweilige Richtung in $x$-, $y$- und $z$-Achse an (manchmal auch als $x_1$-, $x_2$ und $x_3$-Achsen bezeichnet.

Beispiel: Ein Vektor $\vec{a}$ könnte so aussehen:

$$ \vec{a} = \begin{pmatrix} 2 \\ 4 \\ -3 \end{pmatrix} $$

Dieser Vektor bedeutet, du bewegst dich $2$ Einheiten in $x$-Richtung, $4$ Einheiten in $y$-Richtung und $-3$ Einheiten in $z$-Richtung (also nach unten).

Rechenoperationen mit Vektoren

Typische Rechenoperationen in der Vektorrechnung sind die Addition, Subtraktion und skalare Multiplikation.

Vektoraddition und Vektorsubtraktion

Bei der Vektoraddition addierst du die jeweiligen Komponenten der Vektoren:

$$ \vec{a} + \vec{b} = \begin{pmatrix} a_x \\ a_y \\ a_z \end{pmatrix} + \begin{pmatrix} b_x \\ b_y \\ b_z \end{pmatrix} = \begin{pmatrix} a_x + b_x \\ a_y + b_y \\ a_z + b_z \end{pmatrix} $$

Die Vektorsubtraktion erfolgt analog.

Skalare Multiplikation – Vektoren mit Zahlen multiplizieren

Bei der Multiplikation eines Vektors mit einer Zahl (Skalar) verlängerst oder verkürzt du den Vektor:

$$ k \cdot \vec{a} = k \cdot \begin{pmatrix} a_x \\ a_y \\ a_z \end{pmatrix} = \begin{pmatrix} k \cdot a_x \\ k \cdot a_y \\ k \cdot a_z \end{pmatrix} $$

Vektorrechnung Beispiele

Beispiel 1 (Addition):

$\vec{a} = \begin{pmatrix} 2 \\ 3 \\ 1 \end{pmatrix}$ und $\vec{b} = \begin{pmatrix} -1 \\ 0 \\ 4 \end{pmatrix}$

$\vec{a} + \vec{b} = \begin{pmatrix} 2+(-1) \\ 3+0 \\ 1+4 \end{pmatrix} = \begin{pmatrix} 1 \\ 3 \\ 5 \end{pmatrix}$

Beispiel 2 (Skalarmultiplikation):

$3 \cdot \vec{a} = 3 \cdot \begin{pmatrix} 2 \\ 3 \\ 1 \end{pmatrix} = \begin{pmatrix} 3 \cdot 2 \\ 3\cdot 3 \\ 3 \cdot 1 \end{pmatrix}= \begin{pmatrix} 6 \\ 9 \\ 3 \end{pmatrix}$

Wichtige Konzepte und Formeln der Vektorrechnung

Neben Addition und Multiplikation sind das Skalarprodukt, Kreuzprodukt und Linearkombinationen wichtige Konzepte der Vektorrechnung.

Skalarprodukt

Das Skalarprodukt zweier Vektoren gibt an, wie stark zwei Vektoren „miteinander übereinstimmen bzw. voneinander abweichen“.

$$ \vec{a} \cdot \vec{b} = a_x \cdot b_x + a_y \cdot b_y + a_z \cdot b_z $$

Kreuzprodukt (Vektorprodukt)

Das Kreuzprodukt zweier Vektoren liefert einen dritten Vektor, der senkrecht auf den ersten beiden steht.

$$ \vec{a} \times \vec{b} = \begin{pmatrix} a_y b_z - a_z b_y \\ a_z b_x - a_x b_z \\ a_x b_y - a_y b_x \end{pmatrix} $$

Linearkombination

Bei Linearkombinationen multiplizierst du Vektoren mit Zahlen und addierst diese anschließend:

$$ r \cdot \vec{a} + s \cdot \vec{b} = \begin{pmatrix} r a_x + s b_x \\ r a_y + s b_y \\ r a_z + s b_z \end{pmatrix} $$

Anwendungen der Vektorrechnung in der Geometrie

Mit Vektoren kannst du in der Geometrie einfach Geraden oder Ebenen im Raum beschreiben.

Gerade in der Vektorrechnung

$$ g: \vec{x} = \vec{p} + t \cdot \vec{v} $$

Hier ist $\vec{p}$ der Stützvektor und $\vec{v}$ der Richtungsvektor.

Ebene in der Vektorrechnung

$$ E: \vec{x} = \vec{p} + s \cdot \vec{u} + t \cdot \vec{v} $$

Hier verlaufen die zwei Vektoren $\vec{u}$ und $\vec{v}$ in der Ebene, und $\vec{p}$ ist der Stützvektor.

Vektorrechnung – Quiz

Ausblick – das lernst du nach Vektorrechnung

Nach diesen Grundlagen kannst du dein Wissen zu speziellen Themen wie Abstände, Winkelberechnungen oder Lagebeziehungen zwischen Geraden und Ebenen erweitern.

Zusammenfassung zum Thema Vektorrechnung

Vektoren haben eine Länge und eine Richtung.
Typische Operationen sind : Addition, Subtraktion, skalare Multiplikation.
Weitere wichtige Konzepte sind: Skalarprodukt, Kreuzprodukt, Linearkombinationen.
Anwendungen in der analytischen Geometrie: Beschreibung von Geraden und Ebenen.