Sinus, Cosinus und Tangens im rechtwinkligen Dreieck (Trigonometrie)

Inhaltsverzeichnis zum Thema

• Was ist ein rechtwinkliges Dreieck?
• Wie sind der Sinus, Cosinus und Tangens im rechtwinkligen Dreieck definiert?
  • Der Sinus
  • Der Kosinus
  • Der Tangens
  • Die trigonometrischen Funktionen
• Anwendung des Sinus, Kosinus und Tangens
  • Paul am Fluss
  • Der Flächeninhalt eines Drachenvierecks
  • Der trigonometrische Pythagoras

Was ist ein rechtwinkliges Dreieck?

Der Sinus, der Cosinus und der Tangens werden angewendet, um Winkel und Seiten rechtwinkliger Dreiecke zu bestimmen. Woran aber kannst du ein rechtwinkliges Dreieck erkennen?

Ein rechtwinkliges Dreieck ist ein spezielles Dreieck. Es hat einen rechten Winkel, das bedeutet einen Winkel von $90^\circ$. Dieser wird im Dreieck mit einem Punkt im Winkelbogen gekennzeichnet.

• Gegenüber des rechten Winkels befindet sich die längste Seite des rechtwinkligen Dreiecks. Diese wird als Hypotenuse bezeichnet.
• Die beiden übrigen Seiten liegen dem rechten Winkel an. Dies sind die Katheten.
• In Bezug auf einen spitzen Winkel, hier $\alpha$, werden die Katheten als Ankathete sowie Gegenkathete von $\alpha$ bezeichnet.
• Die Gegenkathete ist die Kathete, die dem betrachteten Winkel gegenüberliegt und die Ankathete diejenige, die dem betrachteten Winkel anliegt.

Wie sind der Sinus, Cosinus und Tangens im rechtwinkligen Dreieck definiert?

Der Sinus

Der Sinuswert eines spitzen Winkels in einem rechtwinkligen Dreieck ist der Quotient aus der Länge der Gegenkathete dieses Winkels sowie der Länge der Hypotenuse.

$\sin(\alpha)=\frac{\text{Gegenkathete von }\alpha}{\text{Hypotenuse}}$

Du musst dir also zunächst klarmachen, welche Größen du kennst. Schaue dir hierfür eine Beispielaufgabe an:

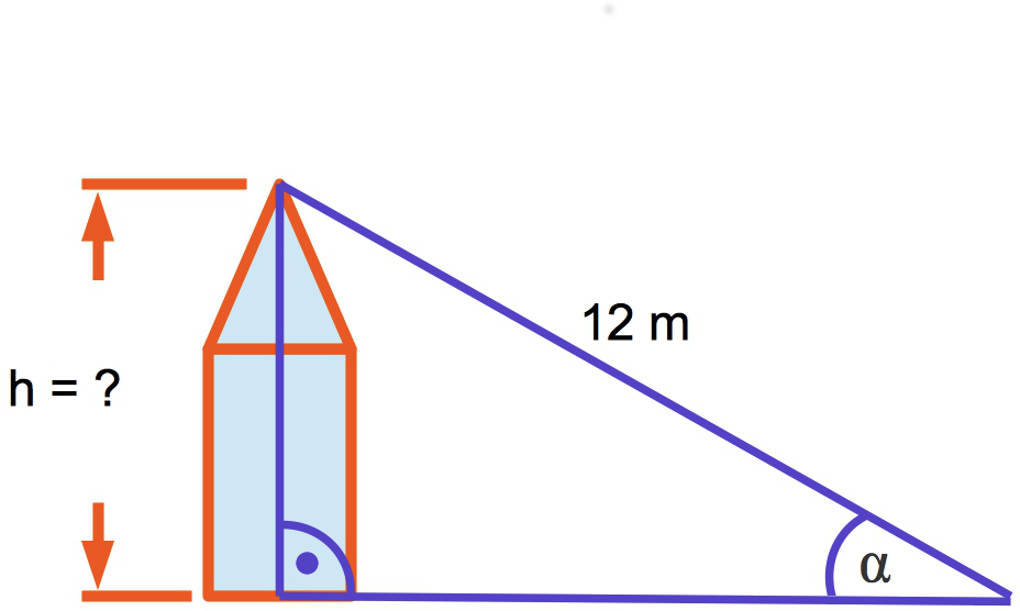
Paul hat eine Skizze von dem Haus gemacht, in dem er wohnt. An das Haus wird eine Leiter der Länge $12~\text{m}$ im Winkel $\alpha=30^\circ$ angelegt.

Du kennst also einen spitzen Winkel und die Länge der Hypotenuse. Die Länge der Gegenkathete des spitzen Winkels möchtest du berechnen: Hier verwendest du den Sinus:

$\sin(30^\circ)=\frac12=\frac h{12~\text{m}}$

Den Sinus von $30^\circ$ zeigt dir dein Taschenrechner an. Du musst noch mit $12~\text{m}$ multiplizieren. So erhältst du für die Höhe des Hauses $h=6~\text{m}$.

Der Kosinus

Der Kosinuswert eines spitzen Winkels ist definiert als der Quotient aus der Länge der Ankathete dieses Winkels sowie der Länge der Hypotenuse.

$\cos(\alpha)=\frac{\text{Ankathete von }\alpha}{\text{Hypotenuse}}$

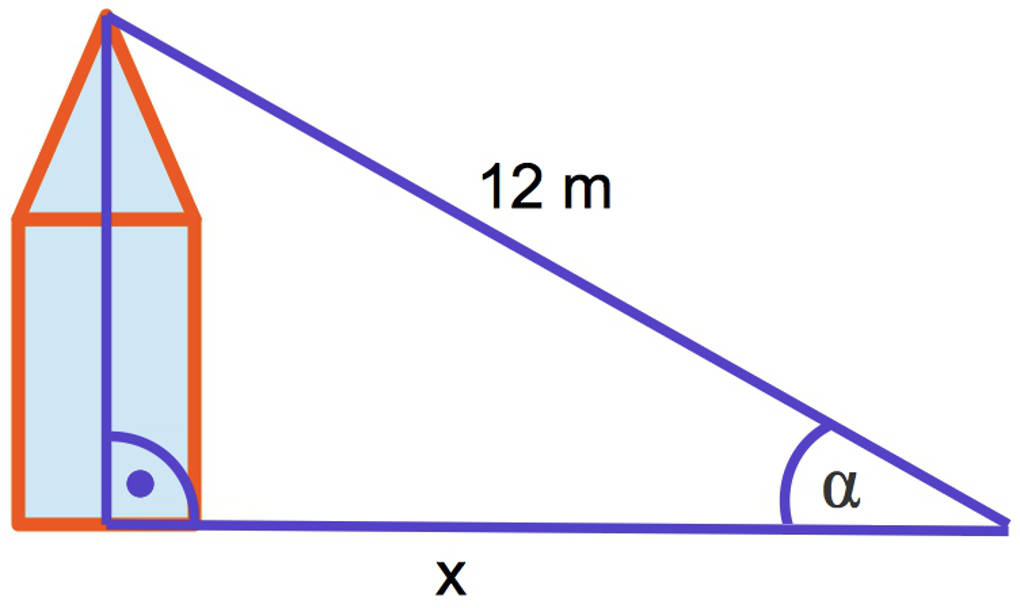
Paul schaut sich die Skizze noch einmal an. Dieses Mal möchte er wissen, wie weit die Leiter von dem Haus entfernt steht. Nun verwendet er den Kosinus:

$\cos(30^\circ)=\frac{\sqrt3}2=\frac x{12~\text{m}}$

Auch hier erhältst du den Wert des Kosinus mit dem Taschenrechner. Multipliziere mit $12~\text{m}$, so erhältst du $x\approx10,4~\text{m}$. Die Leiter steht also ungefähr $10,4~\text{m}$ von der Hauswand weg.

Der Tangens

Der Tangenswert eines spitzen Winkels ist definiert als der Quotient aus der Länge der Gegenkathete sowie der Länge der Ankathete dieses Winkels.

$\tan(\alpha)=\frac{\text{Gegenkathete von }\alpha}{\text{Ankathete von }\alpha}$

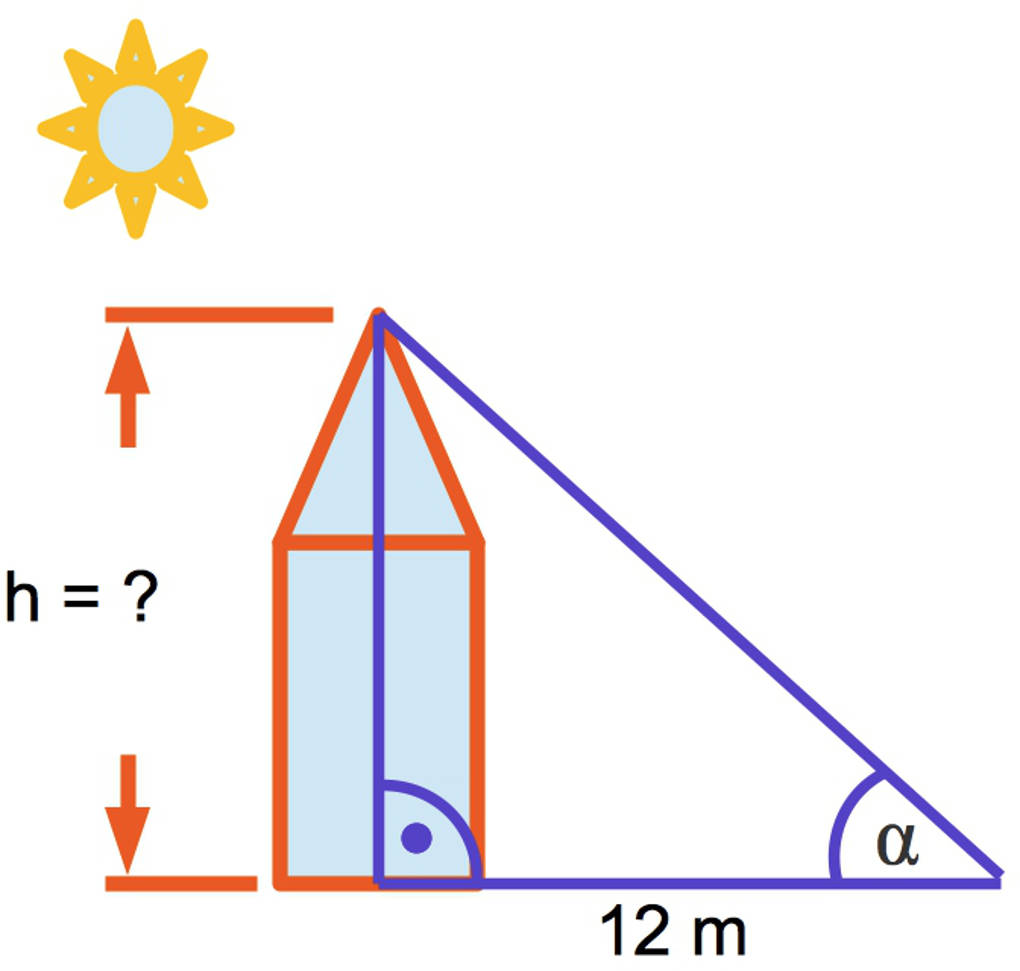
Paul fertigt eine Skizze vom Nachbarhaus an. Die Sonne scheint auf das Haus und wirft einen Schatten der Länge $12~\text{m}$. Er kennt auch noch den spitzen Winkel $\alpha=50^\circ$. Die Länge des Schattens ist die Länge der Ankathete dieses Winkels. Er möchte die Höhe des Hauses, also die Länge der Gegenkathete von $\alpha$ berechnen. Dazu muss er den Tangens verwenden:

$1,192\approx \tan(50^\circ)=\frac h{12~\text{m}}$

Den Tangenswert erhältst du durch Eingabe in deinen Taschenrechner. Multipliziere auch hier mit $12~\text{m}$. Damit erhältst du die Höhe des Hauses $h\approx14,3~\text{m}$.

Du kannst an diesen drei Beispielen bereits erkennen, wie wichtig es ist, dass du

• zum einen die Hypotenuse sowie die An- oder Gegenkathete eines spitzen Winkels erkennen kannst und
• zum anderen bei gegebenen Größen entscheiden kannst, ob du den Sinus oder den Kosinus oder den Tangens verwenden sollst.

Die trigonometrischen Funktionen

Die Sinusfunktion wird ebenso wie die Kosinus- und Tangensfunktion als trigonometrische Funktion bezeichnet.

Anwendung des Sinus, Kosinus und Tangens

Im Folgenden kannst du noch an elementaren Aufgaben üben.

Paul am Fluss

Paul ist mit seinem Freund Luke verabredet. Er überlegt sich, wie lang der Weg über die Brücke und dann am Ufer entlang ist und wie lang der Weg wäre, wenn er direkt zu Luke durch den Fluss schwimmen würde. Er kennt die folgenden Größen:

• Die Brücke ist $8,1~\text{m}$ lang und
• die Entfernung entlang des Flussufers beträgt $25~\text{m}$.

Erst einmal fertigt sich Paul eine Skizze an:

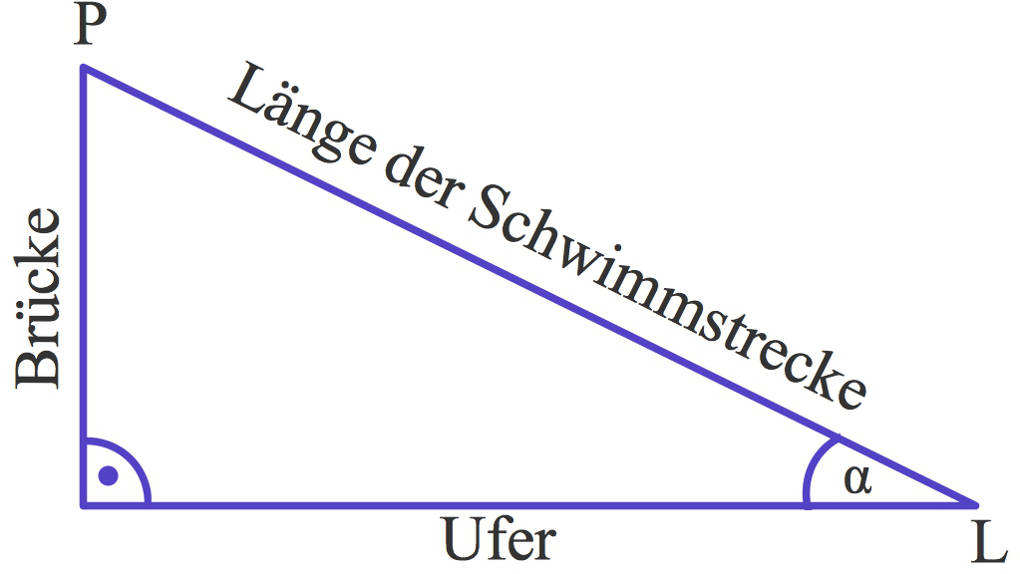
Lass uns einmal mit der Strecke über die Brücke und entlang des Flusses beginnen. Das ist einfach: $8,1~\text{m}+25~\text{m}=33,1~\text{m}$.

Wie lang ist die Schwimmstrecke? Um diese mit den trigonometrischen Funktionen zu bestimmen, musst du erst einmal den spitzen Winkel $\alpha$ berechnen. (Hinweis: Du kannst die Länge auch mit dem **Satz des Pythagoras

Du kennst die Gegen- sowie die Ankathete des spitzen Winkels. Also verwendest du den Tangens:

$\tan(\alpha)=\frac{8,1~\text{m}}{25~\text{m}}=0,324$

Um nun den Winkel zu berechnen, kannst du die $\tan^{-1}$-Taste auf deinem Taschenrechner verwenden. Es ist $\alpha=\arctan(0,324)\approx18^\circ$.

Jetzt kannst du die Länge der Schwimmstrecke berechnen. Dies ist die Hypotenuse in Pauls Skizze. Du kannst dich entscheiden, ob du lieber den Sinus oder den Kosinus verwendest, da du ja sowohl die Gegen- als auch die Ankathete von $\alpha$ kennst.

$\cos(18^\circ)\approx0,951=\frac {25~\text{m}}x$

Multipliziere mit $x$ und dividiere durch $0,951$. Du erhältst dann für die Länge der Schwimmstrecke

$x=\frac{25~\text{m}}{0,951}\approx 26,3~\text{m}$.

Der Flächeninhalt eines Drachenvierecks

Am Fluss möchten Paul und Luke einen Drachen steigen lassen.

Luke bringt den Drachen mit und fragt Paul, ob er berechnen kann, welche Fläche der Drache hat.

Luke erklärt Paul, dass der Drache $1,2~\text{m}$ breit ist und er gibt ihm diese beiden Winkel an: $\alpha=20,6^\circ$ und $\beta=56,3^\circ$.

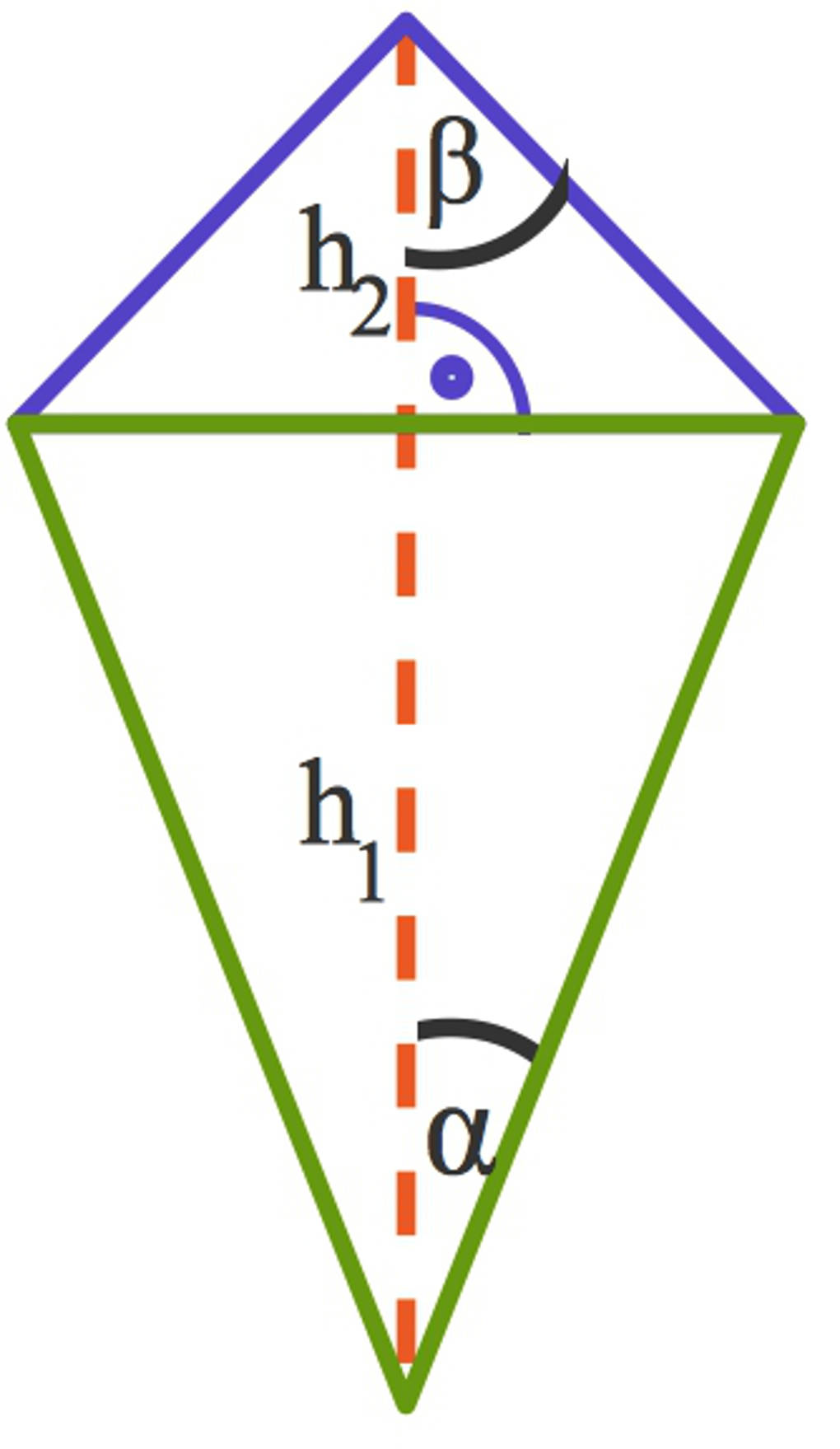
Um die fehlende Höhe des Drachens zu berechnen, verwendet Paul zweimal den Tangens. Dabei berücksichtigt er, dass die Breite des Drachens durch die Höhe halbiert wird. Zusätzlich weiß er, dass die Höhe und die Breite sich in einem rechten Winkel schneiden.

• $\tan(20,6^\circ)=\frac{0,6~\text{m}}{h_1}$: Also ist $h_1=\frac{0,6~\text{m}}{\tan(20,6^\circ)}\approx\frac{0,6~\text{m}}{0,376}\approx 1,6~\text{m}$.
• $\tan(56,3^\circ)=\frac{0,6~\text{m}}{h_2}$: Also ist $h_2=\frac{0,6~\text{m}}{\tan(56,3^\circ)}\approx\frac{0,6~\text{m}}{1,5}= 0,4~\text{m}$.

Damit beträgt die Gesamthöhe des Drachens $h=h_1+h_2=1,6~\text{m}+0,4~\text{m}=2~\text{m}$.

Die Fläche lässt sich berechnen als das Produkt der Hälfte der Breite und der Höhe. Also ist $A=0,6~\text{m}\cdot 2~\text{m}=1,2~\text{m}^2$.

Der trigonometrische Pythagoras

Du kannst dir die trigonometrischen Funktionen auch am Einheitskreis klarmachen.

Im Einheitskreis ist die Länge der Hypotenuse der Radius $r=1$. Damit ist

• $\sin(\alpha)$ die Länge der Gegenkathete und
• $\cos(\alpha)$ die Länge der Ankathete von $\alpha$.
• Übrigens: Die Bedeutung des Tangens kannst du in dem Bild auch erkennen.

Nun gilt nach dem Satz des Pythagoras, dass die Summe der Kathetenquadrate gleich dem Hypotenusenquadrat ist. Also hier:

$(\sin(\alpha))^2+(\cos(\alpha))^2=1$.

Dieser Zusammenhang gilt für jeden beliebigen Winkel $\alpha$ und wird als der trigonometrische Pythagoras bezeichnet.