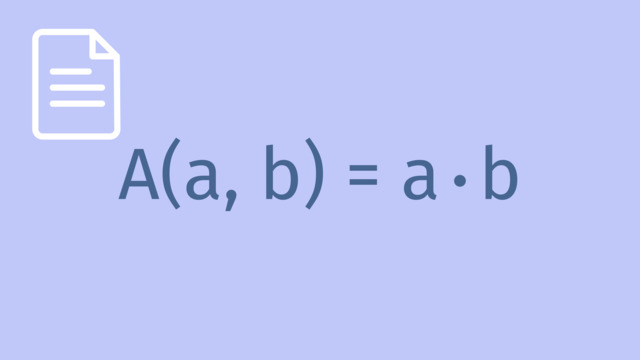Extremwertaufgaben mit quadratischen Funktionen – Anleitung
Um Extremwertaufgaben mit quadratischen Funktionen lösen zu können, ist es wichtig zu verstehen, was eine quadratische Funktion ist und den Unterschied zwischen der allgemeinen und der Scheitelpunktform zu kennen. Danach wirst du lernen, wie man den Scheitelpunkt einer Funktion bestimmt, um Extremwerte wie den maximalen Gewinn oder den minimalen Verbrauch zu ermitteln. Klingt interessant? Dies und vieles mehr erwartet dich im folgenden Text!
- Extremwertaufgaben mit quadratischen Funktionen – benötigtes Vorwissen
- Extremwertaufgaben – Definition
- Allgemeine Vorgehensweise für Extremwertaufgaben
- Extremwertaufgabe – Beispiel Kaninchenstall
- 1. Hauptbedingung aus der Grundsituation aufstellen
- 2. Nebenbedingung aus der Fragestellung aufstellen
- 3. Einsetzungsverfahren nutzen, um eine quadratische Zielfunktion zu erhalten
- 4. Scheitelpunkt der Zielfunktion bestimmen
- Scheitelpunkt über die Nullstellen
- Interpretieren der Informationen
- Extremwertaufgaben mit quadratischen Funktionen – Zusammenfassung
- Häufig gestellte Fragen zum Thema Extremwertaufgaben mit quadratischen Funktionen
in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
5 Minuten verstehen
5 Minuten üben
2 Minuten Fragen stellen
Bereit für eine echte Prüfung?
Lerntext zum Thema Extremwertaufgaben mit quadratischen Funktionen – Anleitung
Extremwertaufgaben mit quadratischen Funktionen – benötigtes Vorwissen
Für dieses Thema solltest du wissen, was eine quadratische Funktion ist. Dazu ist die Unterscheidung zwischen allgemeiner Form und Scheitelpunktform wichtig. Zur kurzen Erinnerung:
Allgemeine Form einer quadratischen Funktionsgleichung:
$y = a \cdot x^{2} + b \cdot x + c$
Scheitelpunktform einer quadratischen Funktionsgleichung:
$y = a \cdot (x~–~d) + e$
Dabei besteht die Besonderheit in der Scheitelpunktform darin, dass der Scheitelpunkt $S(d | e)$ aus der Funktionsgleichung abgelesen werden kann.
Du solltest zudem die folgende Eigenschaft des Scheitelpunkts kennen.
Der Scheitelpunkt einer quadratischen Funktion beschreibt je nach Ausrichtung der Parabel ihren höchsten oder niedrigsten Punkt und damit das Minimum oder Maximum der Funktion.
Extremwertaufgaben – Definition
Extremwertaufgaben werden so genannt, da in ihnen nach dem Extremwert in einer bestimmten Situation gefragt wird. Wie erreicht man den maximalen Gewinn? Was muss man tun, um einen minimalen Verbrauch zu erreichen? Fragen wie diese sind typisch für Extremwertaufgaben. Der Extremwert kann bei quadratischen Funktionen durch den Scheitelpunkt bestimmt werden. Dieser enthält in Form eines Hoch- oder Tiefpunkts den Extremwert als $x$-Koordinate. Wie genau der Scheitelpunkt ermittelt werden kann, wird im Folgenden gezeigt. Extremwertaufgaben werden im Übrigen oftmals auch als Optimierungsaufgaben bezeichnet, da im Sachkontext häufig etwas optimiert werden möchte, wie eben der Gewinn oder Verbrauch.
Allgemeine Vorgehensweise für Extremwertaufgaben
In Extremwertaufgaben geht es insbesondere darum, den gegebenen Sachkontext genau zu verstehen und die nötigen Informationen aus der Aufgabenstellung herauszufiltern. In der Regel wird eine Information gegeben, die Zahlenangaben beinhaltet, und eine Information, die die Fragestellung ausmacht. Dann sieht die Vorgehensweise wie folgt aus:
1. Hauptbedingung aus der Grundsituation aufstellen
2. Nebenbedingung aus der Fragestellung aufstellen
Diese beiden Gleichungen bilden ein lineares Gleichungssystem. Dieses soll nun aber nicht gelöst, sondern zur Erstellung einer Zielfunktion genutzt werden.
3. Einsetzungsverfahren** nutzen, um eine **quadratische Zielfunktion** zu erhalten
4. Scheitelpunkt der Zielfunktion bestimmen
Der letzte Schritt kann auf zwei unterschiedliche Weisen geschehen. Entweder man wandelt die Zielfunktion in die Scheitelpunktform um und liest den Scheitelpunkt ab oder man bestimmt die Nullstellen der Zielfunktion und ermittelt so den Scheitelpunkt. Dieser liegt nämlich immer genau in der Mitte zwischen den beiden Nullstellen. Dieser Scheitelpunkt gibt dann den Extremwert im Sachkontext an. Das klingt in der Theorie alles sehr kompliziert, deswegen schauen wir uns das nun an einem Beispiel an.
Extremwertaufgabe – Beispiel Kaninchenstall
| Aufgabenstellung |
|---|
| Wir wollen einen rechteckigen Kaninchenstall bauen. Insgesamt haben wir $50$ Meter Zaun gekauft. Der Stall soll von allen Seiten umzäunt sein. Mit welchen Seitenmaßen erhalten wir den maximalen Flächeninhalt? |
1. Hauptbedingung aus der Grundsituation aufstellen
Wie lautet die Fragestellung in unserer Sachsituation? Wir wollen den größtmöglichen Flächeninhalt erhalten. Dementsprechend soll der Flächeninhalt maximal werden. Also benötigen wir die Flächeninhaltsformel von Rechtecken als Hauptbedingung:
$A(a,b) = a \cdot b$
$A(a,b)$ verdeutlicht, dass der Flächeninhalt sowohl von der Variable $a$ als auch von der Variable $b$ abhängt.
2. Nebenbedingung aus der Fragestellung aufstellen
Die Grundsituation ist, dass wir $50$ Meter Zaun zur Verfügung haben, der die Stallfläche komplett umzäunen soll. Das bedeutet auch, dass der Umfang des Stallrechtecks $50$ Meter betragen muss. Schließlich wollen wir die ganzen gekauften $50$ Meter Zaun auch zum Umzäunen verwenden. Wir wissen, dass die Umfangsformel für Rechtecke $U = 2a + 2b$ lautet, mit $a$ als Länge und $b$ als Breite des Rechtecks. Dementsprechend können wir also aus den Informationen folgende Nebenbedingung als Gleichung aufstellen:
$50 = 2a + 2b$
Damit haben wir bisher lediglich gesagt, dass der Umfang des Rechtecks $50$ Meter betragen soll. Wir wissen noch nicht, wie groß $a$ und $b$ sind. Wenn der Flächeninhalt irrelevant wäre, könnten wir nun etliche mögliche Wertepaare für $a$ und $b$ benennen. Beispielsweise könnte der Stall $1$ Meter breit und $24$ Meter lang sein. Es fällt jedoch gleich auf, dass das nicht viel Sinn für einen praktikablen Kaninchenstall machen würde. Doch auch die Breite $10$ Meter und die Länge $15$ Meter wären möglich. Das würde schon mehr Sinn ergeben. Da uns aber interessiert, mit welchen Maßen wir den größtmöglichen Flächeninhalt erreichen, müssen wir noch ein paar Schritte weitergehen.
Nun haben wir sowohl unsere Hauptbedingung als auch unsere Nebenbedingung als Gleichungen aufgestellt und alle Informationen aus der Sachaufgabe erfasst.
Achtung: Nutze für beide Gleichungen die gleichen Variablen! Hätten wir zu Anfang in der Hauptbedingung die Seiten des Rechtecks anders benannt, hätten wir dies in der Nebenbedingung fortführen müssen. Ansonsten funktioniert der nächste Schritt nicht.
3. Einsetzungsverfahren nutzen, um eine quadratische Zielfunktion zu erhalten
Nun müssen wir aus den beiden Gleichungen eine machen, damit wir mit dieser weiterarbeiten können. Dazu müssen wir nach dem Einsetzungsverfahren eine der beiden Gleichungen nach einer der gemeinsamen Variablen $a$ oder $b$ umformen, sodass wir diese Gleichung in die andere einsetzen können. Dabei ist es prinzipiell egal, nach welcher Variable umgeformt und auch welche Gleichung in welche eingesetzt wird, man kommt zum gleichen Ergebnis. Der Einfachheit halber wird hier die Nebenbedingung umgeformt und in die Hauptbedingung eingesetzt.
$\begin{array}{rccccccl} 50 & & & = & 2a & + & 2b & | :2 \\ 25 & & & = & a & + & b & | –a \\ 25 & – & a & = & & & b & \\ \end{array}$
Nun wissen wir, dass $b$ das Gleiche ist wie $25~–~a$ und können diese Information in die Hauptbedingung einsetzen:
$A(a) = a \cdot b \Rightarrow A = a \cdot (25~–~a) = 25a~–~a^{2}$
Damit haben wir unsere quadratische Zielfunktion gefunden, die nun nur noch von der Variable $a$ abhängig ist.
4. Scheitelpunkt der Zielfunktion bestimmen
Nun soll der Scheitelpunkt unserer Zielfunktion bestimmt werden. Dazu gibt es, wie oben bereits erläutert, mehrere Wege. Diese sollen im Folgenden vorgestellt werden.
Scheitelpunkt über die Scheitelpunktform
Der Scheitelpunkt kann ermittelt werden, indem die Scheitelpunktform aufgestellt und dann der Scheitelpunkt aus ihr abgelesen wird. Um die Scheitelpunktform aus der allgemeinen Form aufzustellen, muss die quadratische Ergänzung angewandt werden.
$\begin{array}{rcccccccl} A & = & 25a & – & a^{2} & & & & \\ \\ & = & –(a^{2} & – & 25a) & & & & \\ \\ & = & –(a^{2} & – & 25a & + & \frac{625}{4} & – & \frac{625}{4}) \\ \\ & = & –(a^{2} & – & 25a & + & \frac{625}{4}) & + & \frac{625}{4} \\ \\ & = & –(a & – & \frac{25}{2})^{2} & + & \frac{625}{4} & & \\ \\ & = & –(a & – & 12{,}5)^{2} & + & 156{,}25 & & \\ \\ \end{array}$
Nun können wir ablesen, dass der Scheitelpunkt unserer Zielfunktion bei $S(12{,}5 | 156{,}25)$ liegt.
Dadurch dass die Scheitelpunktform $y = a \cdot (x~–~d)^{2} + e$ mit dem Scheitelpunkt $S(d | e)$ lautet, ist hier die $x$-Koordinate des Scheitelpunkts $12{,}5$ und nicht $–12{,}5$.
Scheitelpunkt über die Nullstellen
Weiterhin kann der Scheitelpunkt auch ermittelt werden, indem die Nullstellen der Zielfunktion bestimmt werden. Dies kann wie immer über die pq-Formel oder die Mitternachtsformel geschehen, aber im Fall der Extremwertaufgaben ist es in der Regel leichter, den Satz vom Nullprodukt zu nutzen.
Der Satz vom Nullprodukt besagt, dass ein Produkt immer dann $0$ ist, wenn einer der Faktoren $0$ ist.
Das können wir uns bei der Nullstellenberechnung zunutze machen. Nach dem Einsetzen der einen Gleichung in die andere haben wir nämlich ein Produkt gegeben.
$A(a) = a \cdot (25~–~a)$
$a \cdot (25~–~a)$ ist hier das Produkt, das zur Nullstellenberechnung mit $0$ gleichgesetzt wird. Nach dem Satz vom Nullprodukt müssen wir uns nun die einzelnen Faktoren anschauen. Diese sind hier zum einen $a$ und zum anderen $25~–~a$. Wenn einer davon zu $0$ wird, wird das gesamte Produkt zu $0$. Also sind die Lösungen der Gleichung $0 = a \cdot (25~–~a)$ eben genau die Lösungen der Gleichungen $a = 0$ und $25~–~a = 0$. Damit haben wir unsere beiden Nullstellen $a_1 = 0$ und $a_2 = 25$ gefunden. Der Scheitelpunkt liegt genau in der Mitte dieser beiden Nullstellen. Das liegt daran, dass jede Parabel symmetrisch zu der Gerade ist, die senkrecht durch ihren Scheitelpunkt verläuft. Also liegt der Scheitelpunkt hier bei $a = 12{,}5$.
| Funktionsgraph der Parabelfunktion |
|---|
 |
Die andere Koordinate des Scheitelpunkts lässt sich durch das Einsetzen in die Zielfunktion berechnen:
$A(12{,}5) = 12{,}5 \cdot (25~–~12{,}5) = 12{,}5 \cdot 12{,}5 = 156{,}25$
Interpretieren der Informationen
Was bedeuten nun die Werte $12{,}5$ und $156{,}25$? Es handelt sich um den Scheitelpunkt der Funktionsgleichung $A = –a^{2} + 25a$. Das bedeutet, dass $A = 156{,}25\,\pu{m^2}$ der maximale Flächeninhalt ist, der mit der Seitenlänge $a = 12{,}5\,\pu{m}$ erreicht wird. Durch eine der beiden Bedingungen können wir auch die andere Seitenlänge $b$ berechnen:
$50 = 2a + 2b \Rightarrow 50 = 25 + 2b \Rightarrow b = 12{,}5$
Also erreichen wir den maximalen Flächeninhalt für den Kaninchenstall mit einem quadratischen Stall der Längen $a = 12{,}5\,\pu{m}$ und $b = 12{,}5\,\pu{m}$.
Extremwertaufgaben mit quadratischen Funktionen – Zusammenfassung
Bei der Bearbeitung von Extremwertaufgaben mit quadratischen Funktionen solltest du folgende Schritte befolgen:
- Hauptbedingung als Gleichung aufstellen
- Nebenbedingung als Gleichung aufstellen
- Zielfunktion durch Einsetzen bestimmen
- Scheitelpunkt der Zielfunktion bestimmen
Häufig gestellte Fragen zum Thema Extremwertaufgaben mit quadratischen Funktionen
Extremwertaufgaben mit quadratischen Funktionen – Anleitung Übung
-
Schildere die Vorgehensweise zur Lösung einer Optimierungsaufgabe.
TippsBei Optimierungsaufgaben mit zwei Variablen muss eine Variable in Abhängigkeit der anderen dargestellt werden.
Optimierungsaufgaben werden oft in Form von Textaufgaben gestellt. Du musst aus der Aufgabe herleiten können, wie die Variablen miteinander verbunden sind. Ohne eine solche Angabe ist die Aufgabe nicht lösbar.
Dies führt zu der Hauptbedingung.
Die Zielfunktion $f$ könnte beispielsweise $f(x)=12x-2x^2=-2(x-3)^2+18$ sein.
LösungEine Optimierungsaufgabe ist oft eine Textaufgabe. Wenn dabei 2 Variablen vorkommen, wird wir folgt vorgegangen:
- Aus der Aufgabenstellung kann der Zusammenhang zwischen den Variablen hergeleitet werden. Dies ist die Hauptbedingung.
- Die Fragestellung enthält Teilsätze der Form „damit die Fläche möglichst groß wird“ oder „damit der Materialaufwand möglichst gering wird“. Daraus kann die Nebenbedingung aufgestellt werden.
- Die Hauptbedingung und die Nebenbedingung hängen von den beiden Variablen ab. Die Hauptbedingung wird nach einer der beiden Variablen aufgelöst. Diese Variable wird dann in der Nebenbedingung eingesetzt. Das heißt, man erhält eine Funktion, die nur noch von einer Variablen abhängt: die Zielfunktion.
- Die Zielfunktion ist eine quadratische Funktion. Durch Umformen dieser Funktion in die Scheitelform kann
- der Scheitelpunkt abgelesen werden. Der Scheitelpunkt einer quadratischen Funktion ist
- bei einer nach oben geöffneten Parabel der tiefste Punkt.
- bei einer nach unten geöffneten Parabel der höchste Punkt.
-
Berechne den maximalen Flächeninhalt des Kaninchengeheges.
TippsUte hat $12~m$ Zaun zur Verfügung. Eine Seite des Kaninchengeheges ist die Hauswand.
Das Gehege ist ein Rechteck.
Wie lautet die Formel für den Umfang eines Rechtecks?
Wie lautet die Formel für den Flächeninhalt eines Rechtecks?
Sowohl die Haupt- als auch die Nebenbedingung hängen von 2 Variablen ab.
Die Hauptbedingung wird nach einer der Variablen aufgelöst. Dabei ist es nicht von Bedeutung, nach welcher Variablen aufgelöst wird.
Die Auflösung der Hauptbedingung nach $y$ führt zu $y=12-2x$.
Die Scheitelpunktform der Zielfunktion ist $f(x)=-2(x-3)^2+18$.
Lösung- Ute hat $12~m$ Zaun zur Verfügung. Da das Kaninchengehege ein Rechteck ist, von dem eine Seite die Hauswand ist, führt dies zu der Hauptbedingung $2x+y=12$. Dabei ist $y$ die Seite, die parallel zur Hauswand verläuft. Der Umfang eines Rechtecks ist allgemein $U=2x+2y$.
- Du sollst nun so optimieren, „damit die Fläche möglichst groß wird“. Der Flächeninhalt des gesuchten Rechtecks ist $A=x\cdot y$. Dies ist die Nebenbedingung.
- Die Hauptbedingung und die Nebenbedingung hängen von den beiden Variablen $x$ und $y$ ab. Die Hauptbedingung wird nach $y$ aufgelöst: $y=12-2x$. Diese Variable wird jetzt in der Nebenbedingung eingesetzt: $A=x\cdot (12-2x)$. Man erhält also eine Funktion, die nur noch von einer Variablen abhängt: die Zielfunktion $f(x)=12x-2x^2$.
- Diese quadratische Funktion wird in die Scheitelform umgeformt.
- Aus der Scheitelform kann der Scheitelpunkt $S(3|18)$ abgelesen werden. Die Parabel ist nach unten geöffnet. Deshalb besagt der Scheitelpunkt, dass für $x=3~m$ und damit $y=6~m$ der maximale Flächeninhalt $A=18~m^2$ abgegrenzt werden kann.
$\begin{align*} 12x-2x^2&=-2(x^2-6x)\\ &=-2(x^2-6x+9-9)\\ &=-2((x-3)^2-9)\\ &=-2(x-3)^2+18. \end{align*}$
-
Bestimme den optimalen Eintrittspreis für ein Schwimmbad, der den höchsten Ertrag erbringt.
TippsDie Variable $x$ steht für die Anzahl der Reduktionen des Preises um $0,50~€$ und $y$ für den Eintrittspreis. Das heißt
- $x=1$ liefert $y=5-1\cdot 0,5=4,5$.
- $x=2$ liefert $y=5-2\cdot 0,5=4$.
Rufe dir den Vorgehensplan in Erinnerung.
Zielfunktion, Scheitelpunktsform, Haupt- und Nebenbedingung spielen dabei eine wichtige Rolle.
Stelle die Nebenbedingung auf, welche die Aufgabenstellung wiedergibt. Der Ertrag ergibt sich als Produkt der Besucher mit dem Eintrittspreis.
Die Hauptbedingung gibt an, wie $x$ und $y$ zusammenhängen.
LösungDiese Aufgabe ist etwas komplizierter.
Zunächst werden die Variablen zugeordnet:
- $x$ steht für die Anzahl der Reduktionen des Eintrittspreis. Das heiß: Wie oft wird der Eintrittspreis um $0,50~€$ reduziert?
- $y$ ist der Eintrittspreis.
- $y=5-0,5x$ die Hauptbedingung ist,
- $200+50x$ ist die Anzahl der Besucher nach Reduktion des Eintrittspreises um $x\cdot 0,5~€$.
- Somit ist der Ertrag gegeben durch $E=(200+50x)\cdot (5-0,5x)$.
$\begin{align*} f(x)&=(200+50x)\cdot (5-0,5x)\\ &=1000-100x+250x-25x^2\\ &=-25x^2+150x+1000. \end{align*}$
Diese quadratische Gleichung wird in die Scheitelform umgeformt:
$\begin{align*} -25x^2+150x+1000&=-25(x^2-6x-40)\\ &=-25(x^2-6x+9-9-40)\\ &=-25((x-3)^2-49)\\ &=-25(x-3)^2+1225. \end{align*}$
Der Scheitelpunkt ist also $S(3|1225)$. Dies bedeutet, bei einer Reduktion um $3\cdot 0,5~€$ wird ein maximaler Erlös in Höhe von $1225~€$ erzielt. Es kommen insgesamt $200+50\cdot 3=350$ Besucher.
Gefragt war nach dem optimalen Eintrittspreis. Dieser ist gegeben durch $y=5-0,5\cdot3=3,5$.
Bei einem Eintrittspreis von $3,5~€$ wird ein maximaler Erlös von $1225~€$ erwirtschaftet.
-
Bestimme die Seitenlängen des Rechtecks mit dem maximalen Flächeninhalt.
TippsDer Flächeninhalt eines Rechtecks ist $A=x\cdot y$.
Der Umfang eines Rechtecks ist $U=2x+2y$.
Bei festem Umfang ist zum Beispiel $y=\frac{U-2x}2$.
Die Zielfunktion ist $f(x)=x\cdot \frac{U-2x}2$. Bestimme die Scheitelform und den Scheitelpunkt.
LösungIn dieser Aufgabe ist der Umfang $U=40~cm$ vorgegeben.
- Die Hauptbedingung ist über den festen Umfang gegeben: $2x+2y=40$.
- Zu maximieren ist der Flächeninhalt, also ist die Nebenbedingung $A=x\cdot y$.
- Die Umformung der Hauptbedingung liefert $y=\frac{40-2x}2=20-x$. Dieses $y$ wird in der Nebenbedingung eingesetzt. So erhält man die Zielfunktion $f(x)=x\cdot (20-x)=-x^2+20x$.
- Die quadratische Zielfunktion wird in Scheitelform umgeformt und
- der Scheitelpunkt wird abgelesen.
$\begin{align*} -x^2+20x&=-\left(x^2-20 x+100-100\right)\\ &=-\left(\left(x-10\right)^2-100\right)\\ &=-\left(x-10\right)^2+100. \end{align*}$
Der Scheitelpunkt ist also $S(10|100)$. Was bedeutet dies?
- Es gilt: Für $x=10~cm$ und somit $y=10~cm$ wird der maximale Flächeninhalt $100~cm^2$ angenommen.
- Das heißt, dass die vier Seiten des Rechtecks gleich lang sind. Das flächenmaximale Rechteck ist also ein Quadrat.
- Diese Aussage gilt allgemein: Von allen Rechtecken ist bei festem Umfang das Quadrat das Rechteck mit dem maximalen Flächeninhalt.
-
Zeige die Bedeutung der Scheitelform auf.
TippsDer Graph einer quadratischen Funktion ist eine Parabel. Ist eine Parabel nach
- unten geöffnet, so hat sie einen höchsten Punkt.
- oben geöffnet, so hat sie einen tiefsten Punkt.
Aus der Scheitelform $f(x)=k(x+l)^2+m$ kann der Scheitelpunkt abgelesen werden. Dieser ist $S(-l|m)$. Beachte das vertauschte Vorzeichen in der x-Koordinate.
Dies ist die Parabel zu $f(x)=x^2+2x-1$.
- Sie ist nach oben geöffnet.
- Sie hat den Scheitelpunkt $S(-1|-2)$.
- Dieser Scheitelpunkt ist der tiefste Punkt der Parabel.
LösungEine quadratische Funktion kann in der Normalform, allgemeinen Form, $f(x)=ax^2+bx+c$ oder in der Scheitelform $f(x)=k(x+l)^2+m$ vorliegen.
- Der Faktor $a$ oder $k$ gibt an, ob die Parabel nach oben (für $a>0$ oder $k>0$) oder unten (für $a<0$ oder $k<0$) geöffnet ist. Man kann an diesem Faktor auch erkennen, wie weit die Parabel geöffnet ist.
- Die Scheitelform ist sehr praktisch zum Zeichnen der Parabel, da aus ihr der Scheitelpunkt $S(-m|l)$ ablesbar ist. Er ist im Falle einer nach oben geöffneten Parabel der tiefste und im Falle einer nach unten geöffneten Parabel der höchste Punkt der Parabel. Durch den Scheitelpunkt verläuft die Symmetrieachse der Parabel parallel zur y-Achse.
-
Berechne den minimalen Flächeninhalt.
TippsMach dir eine Skizze des roten Quadrates und zeichne ein innenliegendes Quadrat ein.
Dieses Quadrat schneidet an den 4 Ecken rechtwinklige Dreiecke aus dem roten Quadrat aus.
Sei $x$ die Seitenlänge des innenliegenden Quadrates. Dann ist der Flächeninhalt $A=x^2$.
Den Zusammenhang zwischen $x$ und $y$ erhältst du über den Satz des Phythagoras.
Aus der Scheitelform $f(x)=k(x+l)^2+m$ kann der Scheitelpunkt $S(-l|m)$ abgelesen werden. Beachte den Vorzeichenwechsel in der x-Koordinate des Scheitelpunktes.
LösungJedes Quadrat, welches in das rote Quadrat gelegt wird und dessen Ecken auf dem Rand des roten Quadrates liegen soll, hat die folgenden Eigenschaften:
- Die Seitenlängen sind die Hypotenusen von vier kongruenten, rechtwinkligen Dreiecken, welche aus dem roten Quadrat ausgeschnitten werden.
- Der Flächeninhalt ist das Quadrat dieser Hypotenuse.
- Sei die Seitenlänge des innen liegenden Quadrates $x$ und die eine Kathete $y$, dann ist die andere Kathete $20-y$. Die Summe der beiden Katheten ist die Seitenlänge des roten Quadrates $20~cm$. Nach dem Satz des Pythagoras gilt $x^2=y^2+(20-y)^2$. Dies ist der Flächeninhalt.
Diese kann in die Scheitelform durch quadratische Ergänzung überführt werden:
$\begin{align*} 2y^2-40y+400&=2(y^2-20y+200)\\ &=2(y^2-20y+100-100+200)\\ &=2((y-10)^2+100)\\ &=2(y-10)^2+200. \end{align*}$
Aus der Scheitelform kann der Scheitelpunkt abgelesen werden: $S(10|200)$. Dieser ist der tiefste Punkt der Parabel, da der Faktor vor dem $y^2$ größer ist als $0$. Das bedeutet:
- Für $y=10$ ergibt sich, dass genau in der Mitte der Seiten des roten Quadrates die Eckpunkte des innenliegenden Quadrates liegen und
- der minimale Flächeninhalt $A=200~cm^2$ ist.
8.905
sofaheld-Level
6.601
vorgefertigte
Vokabeln
7.230
Lernvideos
35.784
Übungen
32.546
Arbeitsblätter
24h
Hilfe von Lehrkräften
Inhalte für alle Fächer und Schulstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebeziehungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Quadrat
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Was Ist Eine Viertelstunde
- Prisma
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Satz Des Pythagoras
- Dreieck Grundschule
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Zahlen In Worten Schreiben
- Meter
- Orthogonalität
- Schriftlich Multiplizieren
- Brüche gleichnamig machen
- Brüche Multiplizieren
- Potenzgesetze
- Distributivgesetz
- Bruchgleichungen lösen – Übungen
- Flächeninhalt Dreieck
- Rationale Zahlen
- Volumen Berechnen
