Die Ziege – Extremwertaufgabe mit quadratischer Funktion


in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Grundlagen zum Thema Die Ziege – Extremwertaufgabe mit quadratischer Funktion
Nach dem Schauen dieses Videos wirst du in der Lage sein, Optimierungsprobleme, also Extremwertaufgaben, mit quadratischen Funktionen zu lösen.
Zunächst lernst du, wie du die Angaben der Aufgabe in mathematische Beziehungen überführst. Anschließend geht es darum, aus diesen Beziehungen eine Gleichung zu formulieren, um die Größe zu beschreiben, die optimiert werden soll.

Abschließend erfährst du, wie du diese Gleichung mithilfe einer quadratischen Ergänzung in die Scheitelpunktform bringen kannst und wie daraus die Lösung des Problems gefunden werden kann.

Lerne etwas über das Fressverhalten von Ziegen.
Das Video beinhaltet Schlüsselbegriffe, Bezeichnungen und Fachbegriffe wie Extremwertaufgabe, Extremwert, quadratische Gleichung, Parabel, Scheitelpunkt, Scheitelpunktform, quadratische Ergänzung, binomische Formel und Definitionsbereich.
Bevor du dieses Video schaust, solltest du bereits quadratische Funktionen und die Scheitelpunktform kennen. Außerdem solltest du grundlegendes Wissen zu den binomischen Formeln haben.
Nach diesem Video wirst du darauf vorbereitet sein, weitere Lösungswege für verschiedene Optimierungsprobleme kennenzulernen.
Transkript Die Ziege – Extremwertaufgabe mit quadratischer Funktion
Es gibt Klassiker unter den Matheaufgaben, die wie Märchen oder Fabeln von Generation zu Generation weitergegeben werden. So auch die „Extremwertaufgabe mit der Ziege“, mit der sich wahrscheinlich auch deine Enkel und Urenkel noch herumschlagen werden. Der Plot ist schnell erzählt: Eine Ziege soll auf einer Weide eingezäunt werden, wobei eine Seite schon von einer Mauer begrenzt ist. Für die anderen drei Seiten steht eine bestimmte Länge Zaun zur Verfügung, mit der ein rechteckiges Gehege aufgespannt werden soll. Es gibt nun verschiedene Möglichkeiten, das Gehege zu bilden, zum Beispiel schmal und lang, oder breit und kurz. Jetzt soll aber genau die Möglichkeit gefunden werden, für die die Fläche „A“ des Geheges am größten wird – bei gleichbleibender Gesamtzaunlänge „G“. Es handelt sich um eine „Extremwertaufgabe“, wobei mit „extrem“ in diesem Fall „maximal groß“ gemeint ist. Aber warum Extremwert? Da die Gesamtlänge des Zaunes feststeht, in unserem Fall zum Beispiel „Einhundert Meter“, gibt es nur einen Wert, von dem die Form des Geheges abhängt: Die Breite „x“, die wir wählen, um das Gehege aufzuspannen. Denn daraus ergibt sich auch die Länge „L“ der anderen Seite: Sie ist „Einhundert minus zwei mal x“, wie du hier sehen kannst. Wir könnten natürlich auch die Länge als „x“ definieren und berechnen, wie sich die Breite daraus ergibt. So oder so, alles hängt von einem bestimmten Wert „x“ ab. Wir suchen den Extremwert, also den Wert für „x“, bei dem die Fläche des Geheges maximal wird. Da die Fläche „A“, die wir maximieren wollen, ein Rechteck ist, wird sie aus Länge „L“ mal Breite „x“ berechnet. Hier können wir den gerade aufgestellten Term für „L“ einsetzen und erhalten so eine Gleichung für die Fläche A, die nur von „x“ abhängt. Lass uns die noch ausmultiplizieren und ordnen! Für „x“ können wir nun jeden Wert zwischen Null und Fünfzig einsetzen – das ist sozusagen unser Definitionsbereich. Größer als Fünfzig Meter kann die Breite „x“ nicht werden, denn dann bleibt schon nichts mehr für die Länge des Geheges übrig. Die Fläche wäre in dem Fall allerdings gleich Null. Genauso übrigens, wenn wir „x gleich Null“ wählen. Für welches „x“ wird nun aber „A“ am größten? „A“ ist eine quadratische Funktion, das heißt der zugehörige Funktionsgraph muss eine Parabelform haben. Da der Koeffizient vor dem „x-Quadrat“ negativ ist, handelt es sich um eine nach unten geöffnete Parabel. Die beiden Nullstellen der Parabel sind die beiden eben angesprochenen Fälle: „x gleich Null“ und „x gleich Fünfzig“. Da für diese die Fläche A gleich Null wird. Die Parabel muss also ungefähr SO aussehen! Es kann also nur einen möglichen Maximalwert geben – den Scheitelpunkt der Parabel! Hier ist der größte Funktionswert zu finden – und damit die maximale Fläche A. Nun drängt sich der Verdacht auf, dass dieser Scheitelpunkt genau zwischen den beiden Nullstellen, also bei „x gleich Fünfundzwanzig“ liegen muss. Lass uns das mal überprüfen, indem wir den Funktionsterm der Parabel in die „Scheitelpunktform“ bringen. Dazu brauchen wir ein besonderes Werkzeug: die quadratische Ergänzung. Wir klammern zunächst „Minus-Zwei“ aus, und müssen nun den Term in der Klammer so erweitern, dass wir ihn zu einer binomischen Formel zusammenfassen können. Die zweite binomische Formel passt: Sie bedingt, dass der Koeffizient „Minus-Fünfzig“ gleich „Zwei mal Y“ ist. Also muss „Y gleich Minus-Fünfundzwanzig“ und das fehlende Glied „Y-Quadrat“ demnach „Sechshundertfünfundzwanzig“ sein. Damit erweitern wir also. So können wir diesen Term mit der zweiten binomischen Formel zu „x minus Fünfundzwanzig zum Quadrat“ zusammenfassen, und haben nach dem Ausmultiplizieren der äußeren Klammer die Scheitelpunktform erreicht. Der Scheitelpunkt mit den Koordinaten „Fünfundzwanzig; Eintausendzweihundertfünfzig“ ist schon unsere Lösung. „x gleich Fünfundzwanzig“ ist also tatsächlich die gesuchte Extremstelle, und der Funktionswert „Eintausendzweihundertfünfzig“ ist der gesuchte maximale Flächeninhalt A für dieses „x“. Für unsere Gehege heißt das, dass es mit den verfügbaren einhundert Metern Zaun, genau Fünfundzwanzig Meter breit, und Fünfzig Meter lang gemacht werden soll. Für die Ziege heißt das, dass sie Eintausendzweihundertfünfzig Quadratmeter Platz hat, um sich den Bauch mit Klee vollzuschlagen. Fassen wir nochmal zusammen: Bei einer Extremwertaufgabe soll eine bestimmte Größe, hier die Fläche A, optimiert werden. Die Fläche A wird maximal groß für ein bestimmtes „x“, den gesuchten Extremwert. Aus den Bedingungen und Angaben der Aufgabe ergibt sich hier eine quadratische Gleichung, die die Beziehung zwischen „A“ und „x“ beschreibt. Diese können wir mit Hilfe einer „quadratischen Ergänzung“ in die „Scheitelpunktform“ bringen, und so den Extremwert „x“ sowie die optimierte Größe, also die maximale Fläche, ermitteln. Aus den Angaben der Aufgabe ergeben sich außerdem die Grenzen des Definitionsbereiches. In der Natur finden sich allerdings auch jenseits solcher Grenzen oft verblüffende Lösungen.
Die Ziege – Extremwertaufgabe mit quadratischer Funktion Übung
-
Fasse am Beispiel des Ziegengeheges zusammen, was man unter einer Extremwertaufgabe versteht.
TippsDie Ziegen sollen möglichst viel Platz haben. Die Gesamtlänge des Zauns soll dabei stets gleich sein.
Der Wert, für den die Größe optimal ist, heißt Extremwert.
LösungExtremwertaufgaben:
Bei einer Extremwertaufgabe handelt es sich um ein Optimierungsproblem, das bedeutet, eine Größe soll optimiert werden. Für dieses Problem ist die optimale oder bestmögliche Lösung unter bestimmte Rahmenbedingungen gesucht. Extrem bedeutet hier also beispielweise maximal groß unter den gegebenen Bedingungen.Beispiel Ziegengehege:
Bei dem Problem, ein möglichst großes Ziegengehege zu umzäunen, haben wir die Gesamtlänge des Zauns als Rahmenbedingung gegeben. Der Extremwert $x$ beschreibt die Seitenlänge des rechteckigen Geheges, mit der die maximale Fläche umzäunt wird. Hier steht extrem also für größtmöglich.Hinweis: Bei einer quadratischen Funktion liegt der Extrempunkt immer im Scheitelpunkt. Dabei entspricht die $x$-Koordinate des Scheitels dem Extremwert, die $y$-Koordinate dem optimalen Wert der Größe.
-
Bestimme die maximale Gesamtfläche des Ziegengeheges und die zugehörigen Seitenlängen.
TippsNachdem du die Variablen definiert hast, kannst du die Fläche $A$ und die Länge $l$ mit Termen beschreiben.
Wenn der Term für $A$ nur die Variable $x$ enthält, kannst du ihn in Scheitelpunktform bringen und so die Werte für $x$ und $A$ ablesen.
Erst, wenn du $x$ bestimmt hast, kannst du $l$ berechnen.
LösungDa die Gesamtfläche des umzäunten Ziegengeheges möglichst groß werden soll, handelt es sich um eine Extremwertaufgabe. Um sie zu lösen gehen wir schrittweise vor.
1. Zunächst definieren wir die Variablen $x$ und $l$ für die Seitenlängen sowie $A$ für den Flächeninhalt des Geheges.
2. Wir stellen eine Funktion für $A$ auf, indem wir in die Flächenformel eines Rechtecks $A=a \cdot b$ für die Seitenlängen $x$ und $l = 100 - 2x$ einsetzen: $A = (100 - 2x) \cdot x$
3. Wir multiplizieren aus: $A = -2x^2 + 100x$
4. Wir bringen den Term mittels quadratischer Ergänzung in Scheitelpunktform:
$\begin{array}{rl} A & = -2x^2 + 100x \\ & = -2(x^2 - 50x) \\ & = -2(x^2 - 50x + 25^2 - 25^2) \\ & = -2[(x-25)^2 - 625] \\ & = -2(x - 25)^2 + 1250 \end{array}$
5. Nun können die Koordinaten des Scheitelpunkts abgelesen werden: $S(25 \vert 1250)$
Daraus ergibt sich: $x = 25$ und $A_\text{max} = 1250$
6. Mit $x = 25$ kann $l = 100 - 2x = 100 - 2 \cdot 25 = 50$ berechnet werden.
7. Wir erhalten als Antwort:
Das Gehege hat eine maximale Fläche von $1250~\text{m}^2$, wenn die Seiten $25~\text{m}$ und $50~\text{m}$ lang sind. -
Beschreibe die quadratische Funktion, welche maximiert werden soll.
TippsDa nur drei Seiten geformt werden müssen gilt:
$l = 500-2x$Für den Flächeninhalt des Rechtecks gilt:
$A= l \cdot x$Der Scheitelpunkt liegt in der Mitte des Definitionsbereichs, da dieser durch die Nullstellen der Parabel begrenzt ist.
LösungWir wollen aus einem $500~\text{cm}$ langen Draht drei Seiten eines Rechtecks mit mögllichst großem Flächeninhalt formen. Dabei verwenden wir die Variablen:
- Flächeninhalt $A$
- Seite parallel zur Wand $l$
- Seiten senkrecht zur Wand $x$
Da von den drei Seiten zwei die Länge $x$ haben, gilt für die dritte Seite $l$:
$l = 500-2x$Für den Flächeninhalt des Rechtecks gilt:
$A= l \cdot x$Durch Einsetzen von $l$ und Ordnen, erhalten wir die quadratische Funktion:
$A=(500-2x) \cdot x = 500x-2x^2 = -2x^2+500x$Da für $x = 250$ gilt $l = 0$, hat das Rechteck für $x = 0$ und $x = 250$ jeweils die Fläche $0$. Dies sind die Grenzen des Definitionsbereichs: $[0,250]$.
Das bedeutet, wir können für $x$ Werte zwischen $0$ und $250$ einsetzen.Der Scheitelpunkt liegt genau in der Mitte des Definitionsbereichs, also bei $x=125$.
Wir können dies auch rechnerisch mithilfe der quadratischen Ergänzung überprüfen. Dazu formen wir folgendermaßen um:
$\begin{array}{rl} A(x) & = -2x^2+500x \\ & = -2(x^2-250x) \\ & = -2(x^2 - 2 \cdot 125 \cdot x + 125^2-125^2) \\ & = -2\left[\left(x-125\right)^2 - 125^2\right] \\ & = -2\left[\left(x-125\right)^2 - 15\,625\right] \\ & = -2\left(x - 125\right)^2 + 31\,250 \end{array}$Der Scheitelpunkt lautet also $S(125 \vert 31\,250)$.
Die eine Seitenlänge beträgt somit $125~\text{cm}$, und die andere Seitenlänge $500~\text{cm} - 2 \cdot 125~\text{cm} = 250~\text{cm}$. Damit ergibt sich ein maximaler Flächeninhalt von $31\,250~\text{cm}^2 = 3{,}125~\text{m}^2$.
-
Berechne die größtmögliche Fläche.
TippsEine nach unten geöffnete Parabel hat ihren maximalen Wert im Scheitelpunkt.
Skizziere die Situation und benenne die Variablen, um einen Funktionsterm aufzustellen.
LösungBei Extremwertaufgaben suchen wir nach einem optimalen Wert für eine Größe, zum Beispiel einem maximalen Flächeninhalt.
Beispiel 1:
Das Kaninchengehege von Rudi hat drei Seiten, von denen zwei die Länge $x$ haben. Die dritte Seite, die parallel zur Hauswand verläuft, hat dann die Länge $6 - 2x$, da Rudi insgesamt $6~\text{m}$ Zaun zur Verfügung hat.Für die Fläche des Geheges gilt:
$A = x \cdot (6 - 2x) = -2x^2 + 6x$Wir bringen den Term durch quadratische Ergänzung in die Scheitelpunktform:
$\begin{array}{rl} A & = -2x^2 + 6x \\ & = -2(x^2 - 3x) \\ & = -2(x^2 - 2 \cdot 1{,}5 \cdot x + 1{,}5^2 - 1{,}5^2) \\ & = -2\left[(x^2 - 1{,}5)^2 - 2{,}25\right] \\ & = -2(x^2 - 1{,}5)^2 + 4{,}5 \end{array}$Wir können die Koordinaten des Scheitelpunkts ablesen: $S(1{,}5 \vert 4{,}5)$
Damit ergibt sich als maximale Größe des Geheges: $4{,}5~\text{m}^2$
Beispiel 2:
Der Schwimmbereich wird auf einer Seite durch den Strand begrenzt, die anderen drei Seiten bilden die Begrenzung des Schwimmbereichs. Dabei haben zwei Seiten die Länge $x$, für die dritte Seite verbleiben dann $48 - 2x$, da Bianca insgesamt $48~\text{m}$ der Begrenzung zur Verfügung hat.
Für die Fläche des Schwimmbereichs gilt:
$A = x \cdot (48 - 2x) = -2x^2 + 48x$Wir bringen den Term durch quadratische Ergänzung in die Scheitelpunktform:
$\begin{array}{rl} A & = -2x^2 + 48x \\ & = -2(x^2 - 24x) \\ & = -2(x^2 - 2 \cdot 12 \cdot x + 12^2 - 12^2) \\ & = -2\left[(x^2 - 12)^2 - 144\right] \\ & = -2(x^2 - 12)^2 + 288 \end{array}$Wir können die Koordinaten des Scheitelpunkts ablesen: $S(12 \vert 288)$
Damit ergibt sich als maximale Größe des Schwimmbereichs: $288~\text{m}^2$
-
Gib an, wozu die quadratische Ergänzung genutzt wird.
TippsDie quadratische Ergänzung wird auf quadratische Funktionen angewandt.
Für die Funktion $2x^2 + 4x $ sieht die quadratische Ergänzung folgendermaßen aus:
$\begin{array}{rcl} 2x^2 + 4x & = & 2(x^2 + 2x) \\ & = & 2(x^2 + 2x + 1^2 - 1^2) \\ & = & 2\bigl[(x + 1)^2 - 1\bigr] \\ & = & 2(x + 1)^2 - 2 \end{array}$
Der Scheitelpunkt $S(-1|{-}2)$ kann nun direkt abgelesen werden.
Die Normalform für eine allgemeine quadratische Funktion sieht folgendermaßen aus: $f(x) = ax^2 + bx +c$
Beispiel: $f(x) = 2x^2 + 4x + 7$Die Scheitelpunktform für eine allgemeine quadratische Funktion sieht folgendermaßen aus: $f(x) = a(x - d)^2 + e$
Beispiel: $f(x) = 2(x - 3)^2 + 5$LösungDie quadratische Ergänzung:
Bei der quadratischen Ergänzung wird ein Term so um eine Quadratzahl ergänzt, dass eine binomische Formel entsteht. Dadurch kann ein Funktionsterm, der in Normalform ($ax^2 + bx + c$) vorliegt, in Scheitelpunktform ($a(x - d)^2 + e$) gebracht werden. In dieser Form können die Koordinaten des Scheitelpunktes $S(d \vert e)$ direkt abgelesen werden.Beispiel zur quadratischen Ergänzung:
Wir betrachten die folgende Funktion in Normalform:
$y = x^2 + 6x - 1$
Um eine binomische Formel zu erhalten, müssen wir mit $\left(\frac{6}{2}\right)^2 = 3^2$ ergänzen. Damit der Term dadurch nicht verändert wird müssen wir dieselbe Zahl auch subtrahieren, denn es gilt: $3^2 - 3^2 = 0$.
$y = \overbrace{x^2 + 6x + 3^2}^{\text{binomische Formel}} - 3^2 - 1$
Wir fassen den vorderen Teil mit der binomischen Formel zu $(x+3)^2$ zusammen und verrechnen die restlichen Werte.
$y =(x+3)^2 - 9 - 1 = (x+3)^2 - 10$
Wir erhalten den Funktionsterm in Scheitelpunktform und können die Koordinaten des Scheitelpunkts $S(-3|{-}10)$ direkt ablesen.Folgende Aussage sind somit korrekt:
- Man kann den Scheitelpunkt einer quadratischen Funktion ermitteln.
- Man kann eine quadratische Funktion, die in Normalform vorliegt, in die Scheitelpunktform umformen.
- Man kann die Nullstellen einer linearen Funktion finden.
- Man kann eine quadratische Funktion, die in Scheitelpunktform vorliegt, in die Normalform umformen.
-
Stelle allgemein eine Funktionsgleichung für den Flächeninhalt des Geheges in Abhängigkeit von der Gesamtlänge $u$ des Zauns auf.
TippsStelle zunächst wieder die Beziehung zwischen $l$ und $x$ auf und setze sie in die Funktion $A$ ein. Damit bekommst du eine Funktion, die $x$ und $u$ als Variablen enthält.
Quadratische Ergänzung allgemein:
$\begin{array}{l} \textstyle ax^2 + bx + c \\ ~ \textstyle = a\left(x^2 + \frac{b}{a}x + \frac{c}{a}\right) \\ ~ \textstyle = a\left[x^2 + \frac{b}{a}x + \left(\frac{b}{2a}\right)^2 - \left(\frac{b}{2a}\right)^2 + \frac{c}{a}\right] \\ ~ \textstyle = a\left[\left(x + \frac{b}{2a}\right)^2 - \frac{b^2}{4a^2} + \frac{c}{a}\right] \\ ~ \textstyle = a\left(x + \frac{b}{2a}\right)^2 - \frac{b^2}{4a} + c \end{array}$
LösungHier ist die Gesamtzaunlänge als Parameter $u$ gegeben. Wir führen die Lösungsschritte daher allgemein durch:
Breite des Geheges: $x$
Länge des Geheges: $l = u-2x$
Fläche des Geheges: $A = l \cdot x = (u-2x) \cdot x$Wir wandeln die Formel für die Fläche des Geheges durch quadratische Ergänzung in die Scheitelpunktform um:
$\begin{array}{rl} A & = (u - 2x)x \\ & = -2x^2 +ux \\ & = -2(x^2 - \dfrac{u}{2}x) \\ & = -2\left[x^2 - \dfrac{u}{2}x +\left(\dfrac{u}{4}\right)^2 - \left(\dfrac{u}{4}\right)^2\right] \\ & = -2\left[\left(x - \dfrac{u}{4}\right)^2 - \dfrac{~u^2}{16}\right] \\ & = -2\left(x - \dfrac{u}{4}\right)^2 + \dfrac{~u^2}{8} \end{array}$
Aus der Scheitelpunktform können wir nun den Scheitelpunkt allgemein ablesen:
$S\left(\dfrac{u}{4} \Big| \dfrac{~u^2}{8}\right)$Damit erhalten wir allgemein für die Zaunlänge $u$ einen maximalen Flächeninhalt $A_\text{max} = \dfrac{~u^2}{8}$ mit den Seitenlängen $x = \dfrac{u}{4}$ und $l = \dfrac{u}{2}$.
9.931
sofaheld-Level
6.600
vorgefertigte
Vokabeln
7.800
Lernvideos
37.167
Übungen
32.630
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Schulstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung




 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?
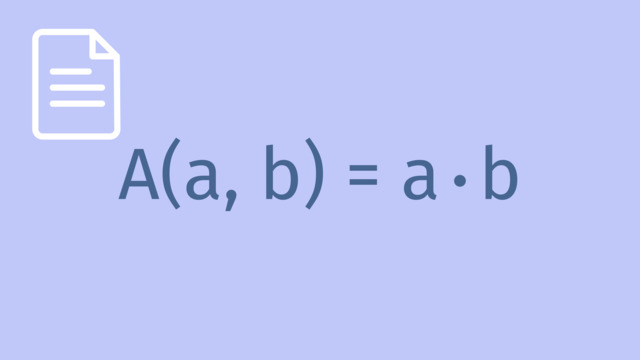










Sehr gutes Video , danke !😊🐐