Rationale Zahlen – Multiplikation und Division
Lerne, wie man rationale Zahlen multipliziert und dividiert, warum das wichtig ist und wie es dir hilft, zum Beispiel Temperaturwerte zu verstehen. Interessiert? Das und vieles mehr findest du im folgenden Text!


in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.

Grundlagen zum Thema Rationale Zahlen – Multiplikation und Division
Rationale Zahlen – Multiplikation und Division – Mathe
Nicht nur im Matheunterricht ist es wichtig zu wissen, wie man rationale Zahlen multiplizieren und dividieren kann. Dies zu können ist zum Beispiel hilfreich, um Temperaturen besser einschätzen und vergleichen zu können, denn bei Temperaturangaben tauchen rationale Zahlen auf.
In diesem Text und Video wird das Multiplizieren und Dividieren von rationalen Zahlen einfach erklärt und du lernst, wie man mal und geteilt durch mit rationalen Zahlen rechnet.
Rationale Zahlen - Wiederholung
Rationale Zahlen sind positive und negative Zahlen, die sich als Bruch darstellen lassen. Dazu gehören also alle ganzen Zahlen und alle Brüche, die jeweils zwischen zwei ganzen Zahlen liegen.
Wie multipliziert man rationale Zahlen?
Die Regeln zum Multiplizieren von rationalen Zahlen sind die gleichen wie zum Multiplizieren von ganzen Zahlen.
- Wenn du zwei positive Zahlen miteinander multiplizierst, erhältst du wieder eine positive Zahl.
- Wenn du zwei negative Zahlen miteinander multiplizierst, erhältst du eine positive Zahl. Dies kannst du dir mithilfe eines Beispiels merken: Die Aussage „Der Film hat mir nicht nicht gefallen.“ bedeutet das Gleiche wie „Der Film hat mir gefallen.“ Eine doppelte Verneinung hebt sich auf und genauso ist es auch in der Mathematik: Minus mal minus ist plus.
- Wenn du eine positive Zahl mit einer negativen Zahl multiplizierst, oder andersherum, so erhältst du eine negative Zahl.
| Beispiele: |
|---|
| $(+2,5)\cdot (+4,2)=+10,5$ |
| $(-2,5)\cdot (-4,2)=+10,5$ |
| $(+2,5)\cdot (-4,2)=-10,5$ |
| $(-2,5)\cdot (+4,2)=-10,5$ |
Wie sieht es aus, wenn wir mehr als zwei Faktoren in unserer Rechnung haben, also wenn wir mehrere rationale Zahlen multiplizieren möchten? Dabei können wir schrittweise vorgehen:
$(-2,5)\cdot (-1,5)\cdot 3,5 = 3,75\cdot 3,5 = 13,125$
Wenn wir in dieser Rechnung ein Minuszeichen weglassen, ergibt sich Folgendes:
$(-2,5)\cdot 1,5\cdot 3,5 = -3,75\cdot 3,5 = -13,125$
Wenn wir die beiden Rechnungen vergleichen, stellen wir fest, dass im ersten Fall zwei negative Zahlen in dem Produkt enthalten waren, im zweiten Beispiel aber nur eine negative Zahl. Es gibt dafür eine allgemeine Regel:
- Ist die Anzahl negativer Faktoren in einem Produkt gerade, so ist das Ergebnis positiv.
- Ist die Anzahl negativer Faktoren in einem Produkt ungerade, so ist das Ergebnis negativ.
Wie dividiert man mit rationalen Zahlen?
Bei der Division sind die Regeln zum Rechnen mit rationalen Zahlen die gleichen wie bei der Multiplikation. Das liegt daran, dass man jede Division durch eine rationale Zahl auf eine Multiplikation zurückführen kann, indem man mit dem Kehrwert multipliziert.
- Wenn du eine positive Zahl durch eine positive Zahl teilst, erhältst du wieder eine positive Zahl.
- Wenn du eine negative Zahl durch eine negative Zahl teilst, erhältst du eine positive Zahl.
- Wenn du eine positive Zahl durch eine negative Zahl teilst, oder andersherum, so erhältst du eine negative Zahl.
Schauen wir uns auch dazu Beispiele an:
Dividieren wir eine Zahl durch einen Bruch, so bilden wir zunächst den Kehrwert des Divisors und multiplizieren dann:
$\left(+\frac{3}{2}\right) : \left(+\frac{8}{3}\right) = \left(+\frac{3}{2}\right) \cdot \left(+\frac{3}{8}\right) = +\frac{9}{16}$
Wir haben also ein positives Ergebnis.
Wie wäre das Ergebnis, wenn wir in der gleichen Rechnung negative Zahlen hätten?
$\left(-\frac{3}{2}\right) : \left(-\frac{8}{3}\right) = \left(-\frac{3}{2}\right) \cdot \left(-\frac{3}{8}\right) = +\frac{9}{16}$
Auch hier erhalten wir eine positive Zahl als Ergebnis.
Nun rechnen wir: $(-10,25):(+5)$. Wir teilen eine negative Zahl durch eine positive, also müssen wir als Ergebnis eine negative Zahl bekommen:
$(-10,25):(+5) = -2,05$
Auch bei Rechnungen mit mehreren Zahlen gilt das Gleiche wie bei der Multiplikation:
- Ist die Anzahl negativer Zahlen bei einer Division gerade, so ist das Ergebnis positiv.
- Ist die Anzahl negativer Zahlen bei einer Division ungerade, so ist das Ergebnis negativ.
Rationale Zahlen multiplizieren und dividieren – Zusammenfassung
Nun hast du die Regeln zum Multiplizieren und Dividieren von rationalen Zahlen kennengelernt und einige Beispiele gesehen.
Bei der Division gelten die gleichen Regeln, weil man jede Division auf eine Multiplikation zurückführen kann, indem man mit dem Kehrwert multipliziert.
Für Rechnungen mit mehreren Zahlen kannst du dir merken:
- Ist die Anzahl negativer Zahlen gerade, so erhält man immer ein positives Ergebnis.
- Ist die Anzahl negativer Zahlen ungerade, so erhält man immer ein negatives Ergebnis.
Nun kannst du überprüfen, wie gut du diese Regeln bereits beherrscht: Schaue dir dazu die interaktiven Übungen und das Arbeitsblatt mit Lösungen zum Thema rationale Zahlen multiplizieren und dividieren auf der Seite an.
Transkript Rationale Zahlen – Multiplikation und Division
Das ist Peter Paket. Er ist Paketbote und wird jeden Tag vor eine neue Herausforderung gestellt. Brr es ist ja dreimal so kalt wie gestern und da waren es schon Minusgrade. Doch als Paketbote muss man auch bei so einem Wetter raus. Und wenn Peter die Multiplikation und Division von rationalen Zahlen versteht, kann er die Temperatur das nächste Mal auch besser einschätzen. Wiederholen wir dazu zunächst einmal, was rationale Zahlen überhaupt sind. Rationale Zahlen sind positive und negative Zahlen, die sich als Bruch darstellen lassen. Auch die ganzen Zahlen sind in der Menge der rationalen Zahlen enthalten. An der Zahlengeraden haben wir also den negativen Bereich, die Null und den positiven Bereich. Wir können Brüche zwischen den ganzen Zahlen eintragen. Der Betrag einer Zahl ist der Abstand dieser Zahl zu 0. So ist der Betrag von -3,5 gleich dem Betrag von 3,5 und das ist gleich 3,5. Schauen wir uns nun die Multiplikation von rationalen Zahlen an. Du weißt ja schon, dass sich bei der Multiplikation von zwei positiven Zahlen ein positives Ergebnis ergibt. Wie sieht es denn bei zwei negativen Zahlen aus? Dort erhält man ebenfalls ein positives Ergebnis. Stell dir mal vor du verneinst eine schon verneinte Aussage, d.h. du sagst zum Beispiel: „Der Film hat mir nicht nicht gefallen“. Das ist ja das gleiche wie „Der Film hat mir gefallen“, also eine positive Aussage. So kannst du dir auch merken, dass minus mal minus plus ergibt. Bei verschiedenen Vorzeichen der Faktoren erhält das Ergebnis das Vorzeichen Minus. Schauen wir uns das doch einmal an ein paar Beispielen an. 2,5 mal 4,2 ist gleich 10,5. Wir multiplizieren zwei positive Zahlen und erhalten ebenfalls ein positives Ergebnis. Minus 2,5 mal minus 4,2 ist ebenfalls 10,5. Wir multiplizieren zwei negative Zahlen und erhalten ebenfalls ein positives Ergebnis. Sowohl minus 2,5 mal 4,2, als auch 2,5 mal -4,2 ergeben -10,5. Bei beiden Rechnungen haben wir jeweils eine positive Zahl und eine negative Zahl. Daher ist auch das Ergebnis negativ. Aber wie sieht es denn bei mehr als zwei Faktoren aus? Wir beginnen mit minus 2,5 mal minus 1,5. Wir haben zwei negative Zahlen, also ein positives Ergebnis. Dann müssen wir nur noch 3,75 mit 3,5 multiplizieren und erhalten 13,125. Aber was passiert, wenn wir bei der gleichen Rechnung ein minus-Zeichen wegnehmen? Wir erhalten zunächst -3,75 und multiplizieren dann mit 3,5. Das Endergebnis ist also negativ. Vergleichen wir diese beiden Rechnungen. Bei der ersten Rechnung hatten wir 2 negative Zahlen und eine positive Zahl, also eine gerade Anzahl an negativen Faktoren. Und bei der zweiten Rechnung 1 negative Zahl und zwei positive Zahlen, also eine ungerade Anzahl an negativen Faktoren. Ist die Anzahl der negativen Zahlen gerade, so erhält man immer ein positives Ergebnis. Ist die Anzahl der negativen Zahlen allerdings ungerade, so erhält man ein negatives Ergebnis. Und wie sieht es bei der Division aus? Auch hier kannst du dir folgende Regeln merken: Dividiert man zwei positive Zahlen, so erhält man auch ein positives Ergebnis. Dividiert man zwei negative Zahlen, so ist auch das Ergebnis positiv. Sind die Vorzeichen unterschiedlich, so erhält man ein negatives Ergebnis. Das ist dasselbe wie bei der Multiplikation, denn du kannst bei den rationalen Zahlen jede Division in eine Multiplikation umschreiben. Schauen wir uns dazu einige Beispiele an. Dividieren wir durch einen Bruch, so schreiben wir die Division zunächst als Multiplikation, indem wir den Kehrwert des Divisors bilden, und multiplizieren dann. Da wir hier zwei positive Zahlen haben, erhalten wir auch ein positives Ergebnis. Wären diese beiden Zahlen negativ, würden wir ebenfalls ein positives Ergebnis erhalten. Was ist denn -10,25 geteilt durch 5? Da wir eine negative Zahl und eine positive Zahl haben, erhalten wir ein negatives Ergebnis. Dies ist auch der Fall, wenn wir 10,25 geteilt durch minus 5 rechnen. Bei der Division mit mehreren Zahlen gelten dieselben Regeln, wie bei der Multiplikation: Ist die Anzahl der negativen Zahlen gerade, so erhält man immer ein positives Ergebnis. Ist die Anzahl der negativen Zahlen ungerade, so erhält man immer ein negatives Ergebnis. Bevor wir sehen, an wen Peter sein Paket heute überhaupt ausliefert, fassen wir zusammen. Bei der Multiplikation und Division von rationalen Zahlen gelten folgende Regeln. Bei gleichen Vorzeichen ist das Ergebnis positiv bei unterschiedlichen Vorzeichen negativ. Multipliziert oder dividiert man rationalen Zahlen, so kann man sich folgendes merken: Ist die Anzahl der negativen Zahlen gerade, so erhält man immer ein positives Ergebnis. Die Regeln sind dieselben, da man jede Division rationaler Zahlen als Multiplikation schreiben kann. Und Peter hat sein Ziel erreicht. Oh, das ist wohl ein ganz besonderer Kunde!
Rationale Zahlen – Multiplikation und Division Übung
-
Berechne die Produkte und Quotienten.
TippsBeachte die Vorzeichenregel Minus mal Minus ergibt Plus.
Das Doppelte von $-4,8$ ist $-9,6$.
Hier ist eine Beispielrechnung:
$ (-2,3) \cdot 3,1 = 2,3 \cdot (-3,1) = - 7,13 $
LösungBei der Multiplikation und Division rationaler Zahlen kannst du zunächst mit den reinen Zahlenwerten rechnen und das Vorzeichen dann mit der Regel Minus mal Minus ergibt Plus bestimmen. Etwas genauer: Ist die Anzahl der Minuszeichen der Fakoren gerade, hat das Produkt das Vorzeichen $+$. Ist die Anzahl der Minuszeichen der Faktoren ungerade, hat das Produkt das Vorzeichen $-$. Bei Divisionen gilt dasselbe.
So erhältst du folgende Gleichungen:
- $(-2,5) \cdot (-4,2) = + 10,5$
- $2,5 \cdot (-4,2) = - 10,5$
- $(-2,5) \cdot (-1,5) \cdot 3,5 = 13,125$
- $(-2,5) \cdot (-1,5) = 3,75$
- $(-10,25) : 5 = - 2,05$
-
Bestimme die Gleichungen.
TippsÜberprüfe die Vorzeichen der beiden Seiten jeder Gleichung.
Die Anzahl an Minuszeichen in einer Gleichung von Produkten oder Quotienten ist auf beiden Seiten gerade oder auf beiden Seiten ungerade.
Folgende Gleichung ist falsch:
$ (-1,1) \cdot (1,1) \cdot (-2) = - 2,42 $
Auf der linken Seite steht eine gerade Anzahl von Minuszeichen, auf der rechten Seite eine ungerade Anzahl.
LösungUm die Gleichungen zu überprüfen, kannst du zuerst auf die Vorzeichen achten: Nach der Regel Minus mal Minus ergibt Plus ist das Produkt zweier negativer Zahlen immer positiv, das Produkt dreier negativer Zahlen immer negativ usw. Stimmen die Vorzeichen beider Seiten einer Gleichung überein, musst du noch die Zahlenwerte rechnerisch überprüfen.
Folgende Gleichungen sind richtig:
- $(-2,5) \cdot (-1,5) = 3,75$
- $3,75 \cdot 3,5 = 13,125$
- $(-2,5) \cdot (-4,2) = 10,5$
- $(-10,25):(-5) \neq -2,05$, denn die Vorzeichen auf beiden Seiten der Gleichung sind nicht konsistent. Tatsächlich ist $(-10,25):(-5) = +2,05$.
- $(-2,5) \cdot (-1,5) \cdot (-3,5) \neq 13,125$, denn $(-2,5) \cdot (-1,5) = 3,75$ und $3,75 \cdot (-3,5) = -13,125$.
- $(-2,5) \cdot (-1,5) \neq 3,5$, denn hier stimmen zwar die Vorzeichen, aber nicht der Zahlenwert. Tatsächlich ist $(-2,5) \cdot (-1,5) = 3,75$.
-
Bestimme die Produkte und Quotienten.
TippsVergleiche die Vorzeichen der beiden Seiten einer Gleichung.
Hier ist eine Beispielrechnung:
$(-5,5) : (-1,1) = 5$
Dividierst du eine Zahl durch einen positiven Dezimalbruch $<1$, so wird die Zahl größer.
LösungBei der Division rationaler Zahlen gilt eine ähnliche Regel wie die Regel Minus mal Minus ergibt Plus für die Multiplikation: Sind Dividend und Divisor beide negativ, ist der Quotient positiv. Ist von Divisor und Dividend nur einer der beiden negativ, der andere positiv, ist der Quotient negativ.
Bei der Rechnung kannst du zunächst mit den reinen Zahlenwerten rechnen und dann die Vorzeichen vergleichen.
So erhältst du folgende Gleichungen:
- $(-1,2) \cdot (-2,3) \cdot (-1,1) = -3,036$
- $(-1,4) \cdot 0,9 \cdot (-1,1) = 1,386$
- $1,2 \cdot (-1,5) \cdot 1,8 = -3,24$
- $1,3 :(-0,2) = -6,5$
- $(-7,2):(-2,4) = 3$
-
Erschließe die rationalen Zahlen.
TippsDas Produkt aus dem Divisor und dem Quotienten einer Division ergibt wieder den Dividenden.
Bei einer Division mit negativen Vorzeichen kannst du zuerst die Division mit den Zahlenwerten mit positiven Vorzeichen ausrechnen und danach das Vorzeichen ergänzen: Sind Dividend und Divisor beide negativ, so ist der Quotient positiv. Sind nur der Divisor oder nur der Dividend negativ, so ist der Quotient ebenfalls negativ.
LösungUm die Aufgabe zu lösen, musst du die fehlenden Terme in den Rechnungen erschließen. Die Rechnungen sind Multiplikationen und Divisionen rationaler Zahlen. Allerdings fehlen nicht immer die Ergebnisse, sondern machmal auch Zwischenschritte, die du aus dem Ergebnis erschließen kannst. Dabei gilt neben der Berechnung der reinen Zahlenwerte immer die Vorzeichenregel Minus mal Minus ergibt Plus.
Du kannst folgende Rechnungen erschließen:
- $(-1,3) : (-0,65) =\Box$: Gesucht ist eine positive Zahl, da auf der linken Seite zwei negative Zahlen multipliziert werden. Den Zahlenwert ermittelst du, indem du $1,3 : 0,65 = 2$ rechnest. Die vollständige Rechnung lautet: $(-1,3) : (-0,65) = +2 = 2$.
- $(1,2) \cdot (\Box)\cdot (-1,5) = 4,14$: Gesucht ist hier eine rationale Zahl, die mit den beiden anderen Faktoren der linken Seite zusammen das Produkt $4,14$ ergibt. Die gesuchte Zahl muss negativ sein, denn auf der linken Seite steht nur eine weitere negative Zahl, auf der rechten Seite der Gleichung aber eine positive Zahl. Den Zahlenwert erhältst du, indem du zunächst die beiden Zahlenwerte links multiplizierst zu $1,2 \cdot 1,5 = 1,8$ und dann die rechte Seite durch $1,8$ dividierst zu $4,14 : 1,8 = 2,3$. Die vollständige Rechnung lautet also: $(1,2) \cdot (-2,3) \cdot (-1,5) = 4,14$.
- $(1,98) : (-0,9) = (\Box)$: Der Quotient auf der rechten Seite muss negativ sein, da der Dividend positiv und der Divisor negativ ist. Du kannst zuerst die Division für die Zahlenwerte ausrechnen und dann das Vorzeichen ergänzen: $1,98:0,9 = 2,2$. Daher lautet die vollständige Rechnung mit den korrekten Vorzeichen: $(1,98) : (-0,9) = (-5,5) \cdot (+0,4) = 2,2$.
-
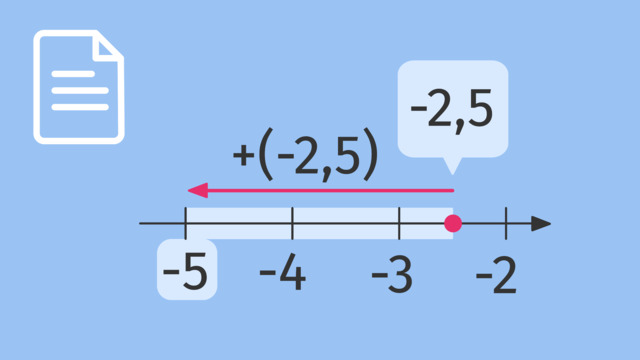
Zeige die rationalen Zahlen auf dem Zahlenstrahl.
TippsJe größer der Zahlenwert einer negativen Zahl ist, desto kleiner ist die Zahl.
Auf der Zahlengeraden stehen die Zahlen nach der Größe geordnet, von links nach recht aufsteigend.
Die rationale Zahl $-\frac{1}{3}$ ist größer als $-1$ und kleiner als $0$.
LösungAuf der Zahlengeraden sind die Zahlen nach der Größe angeordnet: Je kleiner eine Zahl ist, desto weiter links steht sie. Negative Zahlen sind kleiner als $0$ und stehen daher links von $0$ auf dem Zahlenstrahl. Von zwei negativen Zahlen ist jeweils die mit dem größeren Zahlenwert die kleinere Zahl.
Der Abstand zweier benachbarter ganzer Zahlen ist auf der Zahlengeraden immer derselbe. Nicht ganze rationale Zahlen stehen jeweils zwischen zwei ganzen Zahlen. Die Zahl $-\frac{1}{3}$ steht zwischen den Zahlen $-1$ und $0$, die Zahl $\frac{1}{3}$ zwischen $0$ und $1$. Die Zahlen $1,7$ und $-1,7$ haben jeweils denselben Abstand zur $0$. Die Zahl $1,7$ steht zwischen $1$ und $2$. Auch die Zahlen $-3,5$ und $3,5$ haben denselben Abstand zu $0$. Die Zahl $-3,5$ steht rechts der $-4$ und links der $-3$.
-
Berechne die Produkte und Quotienten.
TippsEs gilt:
$(2 \cdot 3) : 4 = 6 : 4 = 1,5$ und $2 \cdot (3:4) = 2 \cdot 0,75 = 1,5$
LösungDu kannst je nach Belieben zuerst die Multiplikationen oder zuerst die Divisionen ausführen und erhältst folgende Gleichungen:
- $(-1,1) \cdot (-2,2) : 0,5 = 4,84 = 4,84 \cdot 0,5 \cdot 2$
- $0,25 \cdot (-4,84) : (-0,2) = 6,05 = 0,5 \cdot (-24,2):(-2)$
- $(-1,3) \cdot (-2,4) :(-1,5) = -2,08 = 4,16:(-2)$
- $(-4,0) \cdot 0,125 \cdot (-4,16) = 2,08 = (-8,32) \cdot (-0,25)$
9.711
sofaheld-Level
6.600
vorgefertigte
Vokabeln
7.787
Lernvideos
37.112
Übungen
32.540
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Schulstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung


 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?

















Das hat‘s richtig gut erklärt, ich schreib in ein paar Tagen einen Test und kann jetzt das super gut!
Thus ist perfekt!
Super erklärt !
Ich finde die Videos sehr hilfreich 😊 🤗 🥹🥹🥹 endlich verstehe ich es ein bisschen mehr 🫶🏻🥳🥳
Die Animation ist super bitte mehr davon