Rationale Zahlen – Addition und Subtraktion
Rationale Zahlen leicht erklärt! In diesem Text erfährst du, wie man rationale Zahlen addiert und subtrahiert. Dazu gibt es hilfreiche Beispiele und Erklärungen mit dem Zahlenstrahl. Kennst du den Unterschied zwischen den Vorzeichen? Neugierig geworden? Das und noch viel mehr wirst du im folgenden Text entdecken!
in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
5 Minuten verstehen
5 Minuten üben
2 Minuten Fragen stellen
Bereit für eine echte Prüfung?
Grundlagen zum Thema Rationale Zahlen – Addition und Subtraktion
Rationale Zahlen – Addition und Subtraktion – Mathe
In diesem Text wird einfach erklärt, wie man rationale Zahlen addieren und subtrahieren kann. Das Addieren und Subtrahieren rationaler Zahlen wird anhand von Beispielen erklärt. Es wird zunächst gezeigt, wie du mithilfe eines Zahlenstrahls rationale Zahlen addieren kannst. Anschließend lernst du die Regeln kennen, welche dir bei der Addition rationaler Zahlen helfen können. Danach wird noch darauf eingegangen, wie du dieses Wissen bei der Subtraktion rationaler Zahlen anwenden kannst.
Rationale Zahlen – Wiederholung
Was sind rationale Zahlen? Alle Zahlen, die als Bruch aus ganzen Zahlen darstellbar sind, gehören zu den rationalen Zahlen.
Der Betrag einer Zahl ist der Abstand dieser Zahl zur Null. So ist der Betrag von $-3,5$ gleich der Betrag von $3,5$ und das ist gleich $3,5$. Wir schreiben das als:
$\vert-3,5\vert = \vert3,5\vert = 3,5$
Beide Zahlen haben den gleichen Abstand zur Null. Die eine Zahl in negativer und die andere Zahl in positiver Richtung.
Um bei der Addition und Subtraktion rationaler Zahlen die Vorzeichen und Rechenzeichen unterscheiden zu können, setzt man eine Klammer um die Zahl mit ihrem zugehörigen Vorzeichen. Das Vorzeichen und die Klammer bei positiven Zahlen werden dabei häufig weggelassen.
Wie addiert man rationale Zahlen?
Betrachten wir für die Addition rationaler Zahlen zunächst das folgende Beispiel:
$1,5 + 2,5$
Beim Addieren einer positiven Zahl geht man auf dem Zahlenstrahl um ihren Betrag nach rechts. In diesem Beispiel müssen wir um $2,5$ von der $1,5$ aus nach rechts gehen.
Wir landen bei der $4$, es gilt:
$1,5 + 2,5 = 4$
Betrachten wir nun die Addition einer negativen Zahl:
$(-2,5) + (-2,5)$
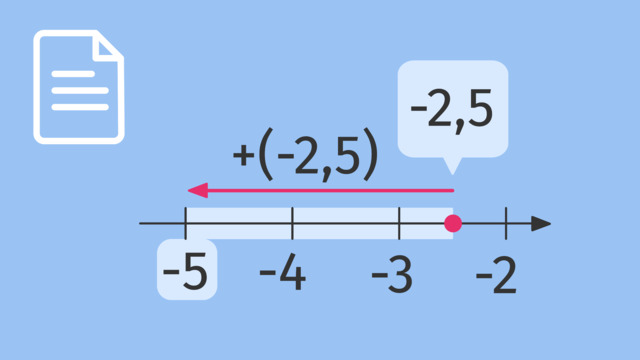
Bei der Addition einer negativen Zahl gehen wir auf dem Zahlenstrahl um ihren Betrag nach links. Wir starten bei der $-2,5$ auf dem Zahlenstrahl und gehen um $2,5$ nach links.
Wir erhalten $-5$, es gilt:
$(-2,5) + (-2,5) = -5$
Betrachten wir ein weiteres Beispiel:
$(-\frac{1}{2}) + 1,5$
Den Bruch können wir umschreiben als $-0,5$. Wir addieren nun eine positive Zahl, gehen also auf dem Zahlenstrahl nach rechts. Bis zur Null sind es $0,5$ Schritte. Bleibt noch ein Schritt übrig. Wir erhalten $1$:
$-\frac{1}{2} + 1,5 = -0,5 + 1,5 = 1$
Betrachten wir eine weitere Aufgabe:
$-5 + 3,5$
Wieder müssen wir uns auf dem Zahlenstrahl nach rechts bewegen. Wir erhalten:
$-5 + 3,5 = -1,5$
Man kann rationale Zahlen auch ohne Zahlenstrahl addieren. Es gibt Regeln, welche dabei helfen, rationale Zahlen geschickt zu addieren. Betrachten wir dafür noch einmal die Aufgaben.
$1,5 + 2,5 = 4$
Es wurden zwei positive Zahlen addiert und das Ergebnis ist ebenfalls positiv.
$(-2,5) + (-2,5) = -5$
Zwei negative Zahlen wurden addiert. Das Ergebnis ist ebenfalls negativ.
$\Rightarrow$ Haben beide Summanden das gleiche Vorzeichen, so hat das Ergebnis ebenfalls dieses Vorzeichen. Die Beträge der Summanden werden addiert.
Bei den folgenden beiden Aufgaben waren die Vorzeichen der Summanden verschieden:
$(-\frac{1}{2}) + 1,5 = 1$
$-5 + 3,5 = -1,5$
Es wurden zwei Zahlen mit verschiedenen Vorzeichen addiert. Die Ergebnisse haben verschiedene Vorzeichen.
$\Rightarrow$ Haben beide Summanden verschiedene Vorzeichen, so hat das Ergebnis dasselbe Vorzeichen wie der Summand, der den größeren Betrag hat. Es wird der kleinere Betrag vom größeren Betrag subtrahiert.
Wie subtrahiert man rationale Zahlen?
Betrachten wir die Subtraktion rationaler Zahlen zunächst wieder anhand des Zahlenstrahls:
Subtrahieren wir eine positive Zahl, so gehen wir den Betrag dieser Zahl nach links.
$3,5 - (+2,5) = 1$
Subtrahieren wir eine negative Zahl, so gehen wir ihren Betrag nach rechts.
$(-3,5) - (-2,5) = -1$
Man kann jede Subtraktion als Addition darstellen, indem man die Gegenzahl des Subtrahenden addiert. Die Gegenzahl ist die Zahl mit gleichem Betrag aber umgekehrten Vorzeichen.
$\Rightarrow$ Man subtrahiert eine rationale Zahl, indem man ihre Gegenzahl addiert.
Es gilt zum Beispiel:
$(-3,5) - (-2,5) = (-3,5) + 2,5$
$(-3,5) - 2,5 = (-3,5) + (-2,5)$
Wie addiert und subtrahiert man rationale Zahlen? – Zusammenfassung
Regeln zum Addieren und Subtrahieren rationaler Zahlen:
Addition:
- Haben die Summanden das gleiche Vorzeichen, so hat auch das Ergebnis das gemeinsame Vorzeichen.
- Haben die Summanden verschiedene Vorzeichen, so subtrahiert man den kleineren Betrag vom größeren Betrag. Das Ergebnis erhält das Vorzeichen des Summanden mit dem größeren Betrag.
Subtraktion:
- Man kann eine rationale Zahl subtrahieren, indem man ihre Gegenzahl addiert. Wir können so die Differenz in eine Summe umschreiben.
Zusätzlich zum Video und dem Text findest du auf der Seite noch Übungen und Arbeitsblätter mit Aufgaben zum Thema rationale Zahlen addieren und subtrahieren.
Transkript Rationale Zahlen – Addition und Subtraktion
Das ist Peter Paket. Er ist Paketbote und wird jeden Tag vor eine neue Herausforderung gestellt. Wie das eine Mal als er bis in den elften Stock gelaufen ist und dann hing ein Schild an der Tür, dass er das Paket 16 Halbe Stockwerke weiter unten abgeben soll. Hier wohnt eindeutig ein Scherzkeks. Um herauszufinden, wo er wirklich hinmuss, muss er Rationale Zahlen addieren und subtrahieren. Wiederholen wir dazu zunächst einmal, was rationale Zahlen überhaupt sind. Rationale Zahlen sind positive und negative Zahlen, die sich als Bruch darstellen lassen. Auch die ganzen Zahlen sind in der Menge der rationalen Zahlen enthalten. An der Zahlengeraden haben wir also den negativen Bereich, die Null und den positiven Bereich. Wir können Brüche und Dezimalbrüche zwischen den ganzen Zahlen eintragen. Der Betrag einer Zahl ist der Abstand dieser Zahl zur 0. So ist der Betrag von Minus 3,5 gleich dem Betrag von 3,5 und das ist gleich 3,5. Beginnen wir mit der Addition und schauen uns dazu dieses Beispiel an: 1,5 + 2,5. 1,5 liegt auf dem Zahlenstrahl hier. Nun wollen wir 2,5 dazu addieren. Wir gehen also 2,5 Schritte in die positive Richtung und erhalten 4. Beim Addieren einer positiven Zahl geht man auf der Zahlengerade also um ihren Wert nach rechts. Aber wie sieht es denn aus, wenn wir eine negative Zahl addieren? Schauen wir uns dazu dieses Beispiel an: minus 2,5 + minus 2,5. Da wir eine negative Zahl addieren, gehen wir dieses mal 2,5 Schritte nach links und erhalten minus 5. Beim Addieren einer negativen Zahl geht man um deren Betrag nach links. Wie sieht es denn bei dieser Aufgabe aus? Minus ein Halb ist das gleiche wie minus 0,5. Wir addieren dann eine positive Zahl, gehen also um ihren Wert nach rechts. Bis zur 0 sind es 0,5 Schritte, bleibt also noch ein Schritt übrig. Wir erhalten 1. Und was ist Minus 5 plus 3,5? Minus 5 liegt hier. Da wir eine positive Zahl addieren, gehen wir 3,5 Schritte nach rechts und erhalten Minus 1,5. Wir müssen uns aber nicht immer einen Zahlenstrahl zur Hilfe nehmen, um rationale Zahlen zu addieren. Schauen wir uns die Rechnungen dazu doch noch einmal genau an, um einige Regeln zu finden. Bei dieser Rechnung haben wir zwei positive Zahlen addiert und ein positives Ergebnis erhalten und hier haben wir zwei negative Zahlen addiert und ein negatives Ergebnis erhalten. Haben die Summanden also das gleiche Vorzeichen, so hat auch das Ergebnis das gemeinsame Vorzeichen. Wir addieren die Beträge und müssen dann nur noch darauf achten, welches Vorzeichen wir vor das Ergebnis setzen. Bei diesen beiden Rechnungen hatten wir jeweils unterschiedliche Vorzeichen, haben aber einmal ein positives Ergebnis und einmal ein negatives Ergebnis. Um herauszufinden, welches Vorzeichen das Ergebnis erhält, müssen wir die Beträge der Summanden miteinander vergleichen. Da 1,5 größer als ein halb ist, haben wir hier ein positives Vorzeichen. Du kannst dir dabei vorstellen, dass du 1,5 minus ein halb gerechnet hast. Weil 5 größer als 3,5 ist, haben wir hier ein negatives Vorzeichen. Das Ergebnis hat nämlich immer das Vorzeichen der Zahl mit dem größeren Betrag. Wie funktioniert denn die Subtraktion bei rationalen Zahlen? Schauen wir uns das zunächst wieder am Zahlenstrahl an. Subtrahieren wir eine positive Zahl, so gehen wir den Betrag dieser Zahl nach links. 3,5 minus 2,5 ist also 1. Subtrahieren wir eine negative Zahl, so machen wir genau das Gegenteil: wir gehen den Betrag der Zahl nach rechts. Minus 3,5 - Minus 2,5 ist also gleich Minus 1. Aber haben wir dann nicht eigentlich addiert? Das Ergebnis ist ja größer als der Minuend. Genau! Du kannst nämlich jede Subtraktion als Addition darstellen, indem du ihre Gegenzahl verwendest. So ist minus 3,5 - minus 2,5 das gleiche wie minus 3,5 plus 2,5. Und Minus 3,5 - 2,5 ist das gleiche wie Minus 3,5 + Minus 2,5. Man kann also eine rationale Zahl subtrahieren, indem man ihre Gegenzahl addiert. Bevor wir sehen, ob Peter es die ganzen Treppenstufen hinunter geschafft hat, um das Paket zuzustellen, fassen wir zusammen. Du kannst dir folgende Regeln merken: Haben die Summanden das gleiche Vorzeichen, so hat auch das Ergebnis das gemeinsame Vorzeichen. Haben die Summanden verschiedene Vorzeichen, dann subtrahiert man den kleineren Betrag vom größeren Betrag. Das Ergebnis erhält das Vorzeichen des Summanden mit dem größeren Betrag. Man subtrahiert eine rationale Zahl, indem man ihre Gegenzahl addiert. Es hilft also die Differenz in eine Summe umzuschreiben. Und Peter hat es geschafft! Da hat er aber nochmal Glück gehabt.
Rationale Zahlen – Addition und Subtraktion Übung
-
Bestimme das Ergebnis.
TippsDie Subtraktion einer Zahl ist dasselbe wie eine Addition mit der Gegenzahl.
Beachte, dass gilt:
$-(-3)=+3$
Beispielrechnung:
$2,\!3-(-1,\!1) = 2,\!3+1,\!1=3,\!4$
LösungBei der Addition positiver Zahlen gehst du auf dem Zahlenstrahl um die entsprechenden Schritte nach rechts, bei der Addition negativer Zahlen nach links.
Bei der Addition von $2,\!5$ gehst du also um $2,\!5$ Schritte nach rechts:
$1,\!5 + 2,\!5 = 4$
Das Ergebnis einer Addition mit $-2,\!5$ liegt um $2,\!5$ Schritte weiter links als die Zahl, zu der du $-2,\!5$ addierst:
$(-2,\!5)+(-2,\!5) = -5$
Bei der Subtraktion ist es genau umgekehrt: Die Subtraktion einer positiven Zahl führt dich um die entsprechenden Schritte nach links, die Subtraktion einer negativen Zahl nach rechts. Insbesondere ist die Subtraktion einer negativen Zahl dasselbe wie die Addition der positiven Gegenzahl:
$3,\!5 -(-2,\!5) = 3,\!5 + 2,\!5 = 6$
Ganz analog ist auch die Addition einer negativen Zahl dasselbe wie die Subtraktion der positiven Gegenzahl.
Einen Bruch kannst du in einen Dezimalbruch umwandeln, um die Rechnung auszuführen:
$-0,\!5+1,\!5=1$
So erhältst du folgende Zuordnung:
- $1,\!5+2,\!5=4$
- $-0,\!5 + 1,\!5 = 1$
- $(-2,\!5)+(-2,\!5) = -5$
- $3,\!5-(-2,\!5) = 6$
-
Nenne ein Zahlenbeispiel, das die Aussage bestätigt.
TippsDie Subtraktion von $-1$ liefert dasselbe Ergebnis wie die Addition von $1$.
Die Gegenzahl hat ein umgekehrtes Vorzeichen.
Beispiel:
$5$ ist die Gegenzahl von $-5$.
LösungBeim Addieren einer positiven Zahl gehst du auf dem Zahlenstrahl nach rechts, beim Subtrahieren nach links. Für negative Zahlen ist es genau umgekehrt: Die Addition einer negativen Zahl führt auf dem Zahlenstrahl nach links, die Subtraktion nach rechts.
Die Gegenzahl einer Zahl ist die betragsgleiche Zahl mit dem umgekehrten Vorzeichen. Der Betrag jeder Zahl außer $0$ ist positiv, denn der Betrag ist genau der Abstand der Zahl zu $0$. Daher haben eine Zahl und ihre Gegenzahl denselben Abstand zu $0$.
So findest du folgende Beispiele:
- Die Addition einer Zahl ergibt dasselbe wie die Subtraktion der Gegenzahl.
$3 + 5 = 3 - ({-}5) = 8$
$4,3+(-1,1) = 4,3 - 1,1 = 3,2$- Die Subtraktion einer negativen Zahl ist dasselbe wie die Addition der positiven Gegenzahl.
$7 - ({-}2) = 7 + 2$
$-1,5 -(-2,3) = -1,5 + 2,3 = 0,8$
$~$- Die Summe zweier positiver Zahlen ist eine positive Zahl.
Beispiel:
$5 + 1 = 6 > 0$
$~$- Die Differenz zweier negativer Zahlen ist nicht notwendigerweise eine negative Zahl. //
Beispiele:
$-2 - ({-}4) = 2 > 0$
$-2,3-(-3,2) = -2,3+3,2 = 0,9$ -
Erschließe die Rechnungen.
TippsDu kannst die Differenz $1,4-5,7$ auch als Summe $1,4+(-5,7)$ schreiben.
Das Ergebnis der Subtraktion $1,4-5,7$ hat ein negatives Vorzeichen, denn:
$|1,4|<|5,7|$
LösungDie Summe positiver Zahlen ist positiv, die Summe negativer Zahlen ist negativ. Bei der Addition von Zahlen mit verschiedenen Vorzeichen hat die Summe dasselbe Vorzeichen wie der betragsgrößte Summand. Um das Vorzeichen einer Differenz zu bestimmen, kannst du die Differenz als Summe schreiben. Dazu musst du nur den Subtrahenden durch seine Gegenzahl ersetzen.
So erhältst du folgende Zuordnungen:
$2,8$:
- $1,3-(-1,5) = 1,3+1,5=2,8$
- $4,1-1,3 = 2,8$
- $(-2,8)-(-5,6) = -2,8-5,6=2,8$
- $3-4,6 =3+(-4,6)=-1,6$
- $-2,8+1,2=-1,6$
- $(-1,8)-(-0,2)=-1,8+0,2=-1,6$
- $2,3+2,4=4,7$
- $5,3-0,6=4,7$
- $(-0,8)-(-5,5)=-0,8+5,5=4,7$
- $3,8-4,1=3,8+(-4,1)=-0,3$
- $(-1,2)+0,9=-0,3$
- $0,3-0,6=0,3+(-0,6)=-0,3$
-
Bestimme die Lösungen.
TippsDu kannst jede Differenz als Summe schreiben, indem du den Subtrahenden durch seine Gegenzahl ersetzt.
Die Gegenzahl von $-1,7$ ist $1,7$.
Hier ist eine Beispielrechnung:
$3,2-(-3,3) = - 3,2+3,3=0,1$
LösungBei der Addition einer positiven Zahl gehst du auf dem Zahlenstrahl nach rechts, bei der Addition einer negativen Zahl nach links. Bei der Addition und Subtraktion von Kommazahlen musst du immer den Übertrag zwischen den Kommastellen beachten. So ist z. B. $0,6 + 0,5 = 1,1$.
Die Addition einer negativen Zahl führt dich auf dem Zahlenstrahl nach links, die Subtraktion nach rechts. Außerdem ist immer die Addition einer Zahl dasselbe wie wie Subtraktion der Gegenzahl.
Die Summe zweier positiver Zahlen ist positiv, die Summe zweier negativer Zahlen ist negativ. Die Summe einer positiven und einer negativen Zahl hat das Vorzeichen der Zahl, deren Betrag größer ist. Um das Vorzeichen einer Differenz zu bestimmen, kannst du die Differenz als Summe schreiben, indem du den Subtrahenden durch seine Gegenzahl ersetzt.
So erhältst du folgende Rechnungen:
- $1,3 +3,8 =5,1$.
- $(-1,1) +(-3,4) =-4,5$.
- $1,2-(-2,1) =3,3$.
- $1,2-2,1=-0,9$.
- $-2,3-(-2,3)=0$.
- $3,4-\frac{3}{2} =1,9$.
-
Benenne die Eigenschaften rationaler Zahlen.
TippsJede natürliche Zahl ist eine rationale Zahl.
Haben zwei Zahlen denselben Betrag, so sind sie gleich oder Gegenzahlen voneinander.
Je weiter eine negative Zahl von $0$ entfernt ist, desto größer ist ihr Betrag.
LösungFolgende Aussagen sind richtig:
- Eine Zahl und ihre Gegenzahl haben denselben Betrag.
- Jede Kommazahl ist eine rationale Zahl.
- Der Betrag einer Zahl ist ihr Abstand zu $0$.
Folgende Aussagen sind falsch:
- Der Betrag einer negativen Zahl ist negativ.
- Jede rationale Zahl liegt zwischen zwei natürlichen Zahlen.
- Jede rationale Zahl ist eine Kommazahl.
-
Bestimme die Lösungen.
TippsDas Ergebnis der Addition $-1,3+5,1$ ist positiv, da $|-1,3|<|5,1|$.
Das Kommutativgesetz der Addition, kann dir helfen, Aufgaben zu vereinfachen:
$a+b=b+a$
LösungDie Summe einer positiven und einer negativen Zahl ist positiv, wenn der Betrag des positiven Summanden größer ist als der Betrag des negativen Summanden. Ist der Betrag des negativen Summanden größer, ist auch die Summe negativ. Haben beide Summanden denselben Betrag, so ist die Summe $0$.
Du kannst jede Differenz als Summe schreiben, indem du den Subtrahenden durch seine Gegenzahl ersetzt. Bei einer Summe mit mehr als zwei Summanden kannst du das Assoziativgesetz verwenden und jeweils zwei Summanden zusammenfassen.
Beispiel:
$1,2-2,1-(-1,7) = (1,2-2,1)+1,7 = (-0,9)+1,7 = 0,8$
Zur Vereinfachung der Rechnungen kannst du auch das Kommutativgesetz der Addition verwenden und die Reihenfolge von Summanden vertauschen. Aber Achtung: Das Kommutativgesetz gilt nur für die Addition, nicht für die Subtraktion!
So findest du folgende Ergebnisse für die vorgegebenen Rechnungen:
Grün
Zuerst kannst du die Rechnung als Summe umschreiben und erhältst:
$-2,3+1,8+3,2-(-2,3) = -2,3+1,8+3,2+2,3$
Mit dem Kommutativgesetz der Addition kannst du die Reihenfolge der Summanden vertauschen:
$-2,3+1,8+3,2+2,3=-2,3+2,3+1,8+3,2$
Mit dem Assoziativgesetz der Addition kannst du die beiden ersten und die beiden letzten Summanden zusammenfassen:
$ \begin{array}{rcl} -2,3+2,3+1,8+3,2 &=& (-2,3+2,3)+(1,8+3,2) \\ &=& 0+5 \\ &=& 5 \end{array} $
Gelb
In dem Term $1,2 -0,75 + \frac{3}{4} -1$ kannst du zunächst den Bruch in einen Dezimalbruch umwandeln:
$1,2 -0,75 + \frac{3}{4} -1 = 1,2 -0,75 + 0,75 -1$
Als Nächstes schreibst du die Differenz als Summe:
$1,2 -0,75 + 0,75 -1 = 1,2+( -0,75) + 0,75 +(-1)$
Nun kannst du mit dem Assoziativgesetz die beiden mittleren Summanden zusammenfassen:
$ \begin{array}{rcl} 1,2+( -0,75) + 0,75 +(-1) &=& 1,2+( -0,75+ 0,75) +(-1) \\ &=& 1,2+(-1) \\ &=& 0,2 \end{array} $
Blau
Bei dem Term $-1,9+\frac{4}{5} +1,1 - 0,4$ schreibst du wieder zuerst den Bruch als Dezimalbuch um:
$-1,9+\frac{4}{5} +1,1 - 0,4 = -1,9+0,8 +1,1 - 0,4$
Jetzt schreibst du die Differenz als Summe:
$-1,9+0,8 +1,1 - 0,4 = -1,9+0,8 +1,1 +(- 0,4)$
Mit dem Assoziativgesetz fasst du die beiden ersten Summanden zusammen:
$ \begin{array}{rcl} -1,9+0,8 +1,1 +(- 0,4) &=& (-1,9+0,8) +1,1 +(- 0,4) \\ &=& (-1,1) + 1,1+(-0,4) \end{array} $
Nun kannst du wieder die beiden ersten Summanden zusammenfassen:
$ \begin{array}{rcl} -1,1 + 1,1+(-0,4) &=& (-1,1+1,1) +(-0,4) \\ &=& 0+(-0,4) \\ &=& -0,4 \end{array} $
Violett
Du kannst wieder zuerst den Bruch in einen Dezimalbruch umwandeln:
$7,3-1,4+\frac{12}{5}-9,2=7,3-1,4+2,4-9,2$
Als Nächstes kannst du die Differenz als Summe schreiben und die beiden mittleren Summanden zusammenfassen:
$ \begin{array}{rcl} 7,3-1,4+2,4-9,2 &=& 7,3+(-1,4)+2,4+(-9,2) \\ &=& 7,3+(-1,4+2,4)+(-9,2) \\ &=& 7,3+1+(-9,2) \end{array} $
Hier kannst du noch einmal die beiden ersten Summanden zusammenfassen:
$ \begin{array}{rcl} 7,3+1+(-9,2) &=& (7,3+1)+(-9,2) \\ &=& (8,3)+(-9,2) \\ &=& -0,9 \end{array} $
8.905
sofaheld-Level
6.601
vorgefertigte
Vokabeln
7.228
Lernvideos
35.778
Übungen
32.540
Arbeitsblätter
24h
Hilfe von Lehrkräften
Inhalte für alle Fächer und Schulstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebeziehungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Quadrat
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Was Ist Eine Viertelstunde
- Prisma
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Satz Des Pythagoras
- Dreieck Grundschule
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Zahlen In Worten Schreiben
- Meter
- Orthogonalität
- Schriftlich Multiplizieren
- Brüche gleichnamig machen
- Brüche Multiplizieren
- Potenzgesetze
- Distributivgesetz
- Bruchgleichungen lösen – Übungen
- Flächeninhalt Dreieck
- Rationale Zahlen
- Volumen Berechnen
Perfekt
Vielen Dank hab es endlich verstanden❤️🌸✨
Toll
Ich hasse mathe doch Sofatutor hilft mir es viel besser zu verstehen
🤫🧏gut