Determinante berechnen
Wenn du die Determinante einer Matrix berechnest, erfährst du, ob sie invertierbar ist. Sie ist auch nützlich für die Flächen- und Volumenberechnung. Möchtest du wissen, wie das funktioniert? Schau dir den folgenden Text an und lerne mehr!
- Determinante einer Matrix
- Determinante berechnen
- Determinante einer $2{\times}2$-Matrix
- Determinante einer $3{\times}3$-Matrix
- Determinante einer $n{\times}n$-Matrix


in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.

Grundlagen zum Thema Determinante berechnen
Determinante einer Matrix
Die Determinante einer quadratischen Matrix ist eine Zahl, die aus den Einträgen der Matrix berechnet werden kann.
Für die Determinante einer Matrix $A$ schreiben wir kurz:
- $\text{det}(A)$ oder
- $\vert A \vert$
Anhand der Determinante kannst du direkt ablesen, ob eine Matrix $A$ invertierbar ist:
- Hat die Determinante von $A$ den Wert $0$ so ist die Matrix nicht invertierbar.
- Gilt dagegen $\text{det}(A) \neq 0$, so kann die Inverse $A^{-1}$ gebildet werden.
Schlaue Idee
Sobald du Informationen über die Invertierbarkeit einer Koeffizientenmatrix hast, weißt du auch, ob das zugehörige lineare Gleichungssystem lösbar ist oder nicht! Das bedeutet, dass du durch das Bestimmen der Determinante direkt eine Aussage über das Gleichungssystem treffen kannst!
Im Folgenden betrachten wir Möglichkeiten zur Berechnung der Determinante. Außerdem zeigen wir dir, wo du die Determinante in Mathe anwenden kannst.
Hinweis: Eine quadratische Matrix ist eine Matrix, die gleich viele Zeilen und Spalten hat, wir können daher auch von einer $n{\times}n$-Matrix sprechen.
Die Determinante ist nur für solche quadratische Matrizen definiert.
Eine quadratische Matrix $A$ mit $2$ (oder $3$) Zeilen und Spalten hat die folgende Gestalt. Eine $[2\times 2]$-Matrix
$A=\begin{pmatrix} a& b \\c&d \end{pmatrix}$
oder eine $[3\times 3]$-Matrix
$A=\begin{pmatrix} a&b&c \\ d&e&f\\ g&h&i \end{pmatrix}$
Determinante berechnen
Je nach Dimension einer quadratischen Matrix gibt es verschiedene Möglichkeiten die Determinante zu berechnen.
Hat eine Matrix nur einen Eintrag, so entspricht dieser auch dem Wert der Determinante:
Für $A = \begin{pmatrix} a \end{pmatrix}$ ist $\text{det}(A) = a$.
Determinante einer $2{\times}2$-Matrix
Die Determinante einer $2{\times}2$-Matrix kannst du in zwei Schritten berechnen.

- Du multiplizierst die Elemente der Hauptdiagonalen, von oben links nach unten rechts, und
- subtrahierst davon das Produkt der Elemente der Nebendiagonalen, von unten links nach oben rechts.
Formel für die Determinante einer $2{\times}2$-Matrix:
$\text{det}\begin{pmatrix} a& b \\c&d \end{pmatrix}=\begin{vmatrix} a & b \\ c & d \end{vmatrix} = a \cdot d - c \cdot b$
Lass uns dies einmal an einem Beispiel üben.
$\begin{vmatrix} 2 & 3 \\ 4 & -1 \end{vmatrix} = 2\cdot ({-}1)-4\cdot 3=-2-12=-14$
Übrigens ist die Determinante einer Matrix $0$, wenn eine Zeile ein Vielfaches der anderen ist. Hier ein Beispiel:
$\begin{vmatrix} 2 & 4 \\ -1 & -2 \end{vmatrix} = 2\cdot ({-}2) - ({-}1) \cdot 4 = -4 - ({-}4) = -4 + 4 = 0$
Determinante einer $3{\times}3$-Matrix
Auch zur Berechnung der Determinante einer $3{\times}3$-Matrix verwendest du die Haupt- und Nebendiagonalen der Matrix. Die Regel ist nach dem französischen Mathematiker Pierre Frédéric Sarrus benannt.
Regel von Sarrus in Worten:
- Du multiplizierst die Einträge der erweitereten Matrix von oben links nach unten rechts und addiertst die Produkte.
- Davon subtrashierst du die Produkte der Einträge der erweiterten Matrix, die du von unten links nach oben rechts multiplizierst.
Regel von Sarrus – Formel
$\begin{array}{rccccccc} \begin{array}{|ccc|cc} a & b & c & \color{dodgerblue}{a} & \color{dodgerblue}{b} \\ d & e & f & \color{dodgerblue}{d} & \color{dodgerblue}{e} \\ g & h & i & \color{dodgerblue}{g} & \color{dodgerblue}{h} \end{array} & = && a \cdot e \cdot i &+& b \cdot f \cdot g &+& c \cdot d \cdot h \\ &&-& g \cdot e \cdot c &-& h \cdot f \cdot a &-& i \cdot d \cdot b \end{array}$

Wir berechnen zwei Beispiele mit Hilfe der Regel:
$\begin{array}{rrcl} \bullet & \begin{array}{|rrr|rr} 2 & 5 & -1 & \color{dodgerblue}{2} & \color{dodgerblue}{5} \\ -3 & 1 & 0 & \color{dodgerblue}{-3} & \color{dodgerblue}{1} \\ 4 & -2 & 2 & \color{dodgerblue}{4} & \color{dodgerblue}{-2} \end{array} & = & 2 \cdot 1 \cdot 2 + 5 \cdot 0 \cdot 4 + ({-}1) \cdot ({-}3) \cdot ({-}2) \\ &&& - 4 \cdot 1 \cdot ({-}1) - ({-}2) \cdot 0 \cdot 2 - 2 \cdot ({-}3) \cdot 5 \\ \\ && = & 4 + 0 + ({-}6) - ({-}4) - 0 - ({-}30) \\ \\ && = & \underline{\underline{32}} \end{array}$
$\begin{array}{rrcl} \bullet & \begin{array}{|rrr|rr} 3 & -1 & 2 & \color{dodgerblue}{3} & \color{dodgerblue}{-1} \\ 1 & 1 & 2 & \color{dodgerblue}{1} & \color{dodgerblue}{1} \\ 2 & 1 & -1 & \color{dodgerblue}{2} & \color{dodgerblue}{1} \end{array} &=& 3\cdot 1\cdot (-1) + ({-}1) \cdot 2 \cdot 2 + 2 \cdot 1\cdot 1 \\ &&& - 2 \cdot 1 \cdot 2 - 1 \cdot 2 \cdot 3 - ({-}1) \cdot 1 \cdot ({-}1) \\ \\ &&=& -3 - 4 + 2 - 4 - 6 - 1 \\ \\ &&=& \underline{\underline{-16}} \end{array}$
Fehleralarm
Vergiss nicht, dass das Produkt auf der Nebendiagonalen abgezogen wird. Das bedeutet, dass diese Terme ein negatives Vorzeichen haben! Benutze Klammern, falls du negative Einträge in der Matrix hast, damit du dich nicht selbst verwirrst.
Determinante einer $n{\times}n$-Matrix
Die Determinante einer $n{\times}n$-Matrix kann ganz allgemein auch mit dem Laplace'schen Entwicklungssatz berechnet werden. Dabei wird die Determinante entweder spalten- oder zeilenweise entwickelt.
Zum Beispiel kannst du die Determinante der zweiten $3{\times}3$-Matrix von oben auch mit der ersten Spalte entwickeln:
- Du multiplizierst das $(-1)^{i+1}$-fache des Elementes in der $i$-ten Zeile und ersten Spalte mit der Determinante der Untermatrix, welche entsteht, wenn du aus der Ausgangsmatrix die $i$-te Zeile und erste Spalte streichst.
- Dieses Produkt berechnest du für jedes Element in der ersten Spalte und
- addierst die Produkte.
$\begin{array}{rcl} \begin{vmatrix} \color{gold}{3} & -1 & 2 \\ \color{gold}{1} & 1 & 2 \\ \color{gold}{2} & 1 & -1 \end{vmatrix} & = & ({-}1)^{1+1} \cdot \color{gold}{3} \color{#666666}{~\cdot~} \begin{vmatrix} 1 & 2 \\ 1 & -1 \end{vmatrix} + ({-}1)^{2+1} \cdot \color{gold}{1} \color{#666666}{~\cdot~} \begin{vmatrix} -1 & 2 \\ 1 & -1 \end{vmatrix} + ({-}1)^{3+1} \cdot \color{gold}{2} \color{#666666}{~\cdot~} \begin{vmatrix} -1 & 2 \\ 1 & 2 \end{vmatrix} \\ \\ &=& 3 \cdot ({-}1-2) -1 \cdot (1-2) + 2 \cdot ({-}2-2) \\ \\ &=& -9 + 1 - 8 \\ \\ &=& \underline{\underline{-16}} \end{array}$
Wie du siehst, erhalten wir den gleichen Wert für die Determinante.
Mit dem Laplace'schen Entwicklungssatz kannst du die Determinante einer beliebigen quadratischen Matrix schrittweise berechnen.
Dabei reduziert sich mit jeder Anwendung des Entwicklungssatzes die Anzahl der Zeilen und Spalten der Matrizen, deren Determinanten berechnet werden müssen, um eins.
So reduzierst du die Berechnung der Determinante einer
Determinante – Eigenschaften und Rechenregeln
Für die Determinante einer $n{\times}n$-Matrix $A$ gilt:
- Determinante der Transponierten $A^{\text{T}}$ (Zeilen und Spalten vertauscht):
$\text{det}(A^{\text{T}})$ = $\text{det}(A)$ - Determinante der Inversen $A^{-1}$:
$\text{det}(A^{-1}) = \dfrac{1}{\text{det}(A)}$ - Determinante des Produkts mit einem Skalar $a \in \mathbb{R}$:
$\text{det}(a \cdot A) = a^n \cdot \text{det}(A)$ - Determinante des Produkts mit einer $n{\times}n$-Matrix $B$:
$\text{det}(A \cdot B) = \text{det}(A) \cdot \text{det}(B)$ - Bei Vertauschung von zwei Zeilen oder Spalten ändert sich lediglich das Vorzeichen der Determinante.
- Wird eine einzelne Zeile oder Spalte der Matrix mit einem Faktor $a \in \mathbb{R}$ multipliziert, so ändert sich auch die Determinante um diesen Faktor.
- Bei Addition eines Vielfachen einer Zeile oder Spalte zu einer anderen Zeile oder Spalte bleibt der Wert der Determinante unverändert.
Determinante – Anwendung
Im Folgenden betrachten wir die wichtigsten Anwendungen der Determinante.
Flächenberechnung mit Determinante
Du kannst durch die Berechnung der Determinante einer $2{\times}2$-Matrix die Fläche einer ebenen Figur berechnen.
Flächeninhalt Parallelogramm – Herleitung
Um zu verstehen, wie wir die Determinante und der Flächeninhalt eines Parallelogramms zusammenhängen, betrachten wir die folgende Abbildung:
Wir wollen den Flächeninhalt $A$ des Parallelogramms $ABCD$ bestimmen. Es wird durch die zwei Vektoren $\vec{a} = \overrightarrow{AB} = \overrightarrow{DC}$ und $\vec{b} = \overrightarrow{AD} = \overrightarrow{BC}$ aufgespannt. Die beiden Vektoren können wir in der Komponentenschreibweise auch folgendermaßen aufschreiben:
$\vec{a} = \begin{pmatrix} a_x \\ a_y \end{pmatrix} \quad$ und $\quad \vec{b} = \begin{pmatrix} b_x \\ b_y \end{pmatrix}$
Wenn wir ein Rechteck mit den Eckpunkten $A$, $E$, $C$ und $F$ um das Parallelogramm zeichnen, können wir die Seiten des Rechtecks jeweils als Summe der Komponenten der Vektoren darstellen. Die Seite $\overline{AF}$ setzt sich beispielsweise aus den Komponenten $b_y$ und $a_y$ zusammen.
Mit den eingezeichneten Vektorkomponenten ergeben sich sechs weitere, kleine Flächen, die das Parallelogramm umgeben. Um die Fläche des Parallelogramms zu bestimmen, können wir daher die Gesamtfläche des Rechtecks $A_{\text{Ges}}$ berechnen und diese sechs Flächen abziehen.
Die Fläche des Rechtecks berechnen wir folgendermaßen:
$\begin{array}{rcl} A_{\text{Ges}} &=& (a_x + b_x) \cdot (a_y + b_y) \\ \\ &=& a_x \cdot a_y + a_x \cdot b_y + b_x \cdot a_y + b_x \cdot b_y \end{array}$
Um die Fläche des Parallelogramms zu erhalten, müssen wir jetzt die sechs kleineren Flächen abziehen. Zunächst betrachten wir das blau schraffierte rechtwinklige Dreieck. Seine Katheten haben die Längen $b_y$ und $b_x$. Das Dreieck hat damit die Fläche:
- $A_{\color{blue}{\triangle}} = \frac{1}{2} \cdot b_y \cdot b_x$
Das gelb schraffierte Dreieck hat Katheten der Länge $a_y$ und $a_x$ und die Fläche:
- $A_{\color{gold}{\triangle}} = \frac{1}{2} \cdot a_y \cdot a_x$
Das rot schraffierte, kleine Rechteck hat die Seitenlängen $a_y$ und $b_x$ und folglich den Flächeninhalt:
- $A_{\color{red}{\square}} = a_y \cdot b_x$
Da die zwei Dreiecke und das Rechteck unter dem Parallelogramm exakt dieselben Maße haben und lediglich gespiegelt sind, müssen wir die drei so bestimmten Flächeninhalten jeweils zweimal abziehen:
$A_{\text{Parallelogramm}} = A_{\text{Ges}} - 2 \cdot A_{\color{blue}{\triangle}} - 2 \cdot A_{\color{gold}{\triangle}} - 2 \cdot A_{\color{red}{\square}}$
Wir setzten ein und fassen gleichnamige Terme zusammen:
$\begin{array}{rcl} A_{\text{Parallelogramm}} &=& a_x \cdot a_y + a_x \cdot b_y + b_x \cdot a_y + b_x \cdot b_y - b_y \cdot b_x - a_y \cdot a_x - 2 \cdot a_y \cdot b_x \\ &=& a_x \cdot a_y - a_x \cdot a_y + a_x \cdot b_y + b_x \cdot b_y - b_x \cdot b_y + a_y \cdot b_x - 2 \cdot a_y \cdot b_x \\ &=& a_x \cdot b_y - a_y \cdot b_x \end{array}$
Weil mehrere Terme sowohl mit positivem als auch negativem Vorzeichen auftreten, addieren sie sich zu null und fallen weg. Wir erhalten somit:
$A_{\text{Parallelogramm}} = a_x \cdot b_y - a_y \cdot b_x$
Das entspricht der Determinante einer $2{\times}2$-Matrix:
$A_{\text{Parallelogramm}} = \text{det}\begin{pmatrix} a_x & b_x \\ a_y & b_y \end{pmatrix} = a_x \cdot b_y - a_y \cdot b_x$
Die Matrix $\begin{pmatrix} a_x & b_x \\ a_y & b_y \end{pmatrix}$ enthält die Vektoren $\vec{a}$ und $\vec{b}$, die den Seiten des Parallelogramms entsprechen, als Spalten. Die Determinante ist aber nur dann gleich dem Flächeninhalt des von den Vektoren aufgespannten Parallelogramms, wenn zwei Bedingungen erfüllt sind:
- Die beiden Vektoren müssen denselben Fußpunkt haben.
- Der Vektor in der ersten Spalte der Matrix muss – in der Zeichnung gegen den Uhrzeigersinn zu dem Vektor der zweiten Spalte gedreht – die Fläche des Parallelogramms überstreichen.
Sind diese Bedingungen nicht erfüllt, kann man die Determinante zwar trotzdem berechnen, sie kann aber einen negativen Wert liefern, der dann im Betrag dem Flächeninhalt des Parallelogramms entspricht.
Flächeninhalt Dreieck
Wenn du ein Dreieck an einer seiner Seiten spiegelt, erhältst du ein Parallelogramm, dessen Flächeninhalt genau doppelt so groß ist, wie der des Dreiecks. Entsprechend hat das Dreieck genau den halben Flächeninhalt des Parallelogramms. Wir können also auch hier die Formel für den Flächeninhalt eines Parallelogramms mit der Determinante aus dem letzten Kapitel nutzen.
$A_{\text{Dreieck}} = \dfrac{1}{2} \cdot \left\vert\text{det}\begin{pmatrix} a_x & b_x \\ a_y & b_y \end{pmatrix}\right\vert = \dfrac{1}{2} \cdot \vert a_x \cdot b_y - a_y \cdot b_x \vert$
Auch hier sind die Koeffizienten der Matrix die Einträge von Vektoren, die Seiten des Dreiecks beschreiben.
Volumenberechnung mit Determinante
Ein Spat oder auch Parallelepiped ist ein geometrischer Körper. Die begrenzenden Flächen sind paarweise kongruente, in parallelen Ebenen liegende Parallelogramme. Hier siehst du einen Spat.

Dieser Spat wird von den drei Vektoren $\vec a$, $\vec b$ und $\vec c$ aus dem $\mathbb{R}^3$ aufgespannt.
Das Volumen eines solchen Spats ist gegeben durch das Spatprodukt:
$V_{\text{Spat}}=\left|\left(\vec a\times\vec b\right)\cdot \vec c \right| $
Dieses Spatprodukt ist der Betrag der Determinante der $3{\times}3$-Matrix, welche entsteht, wenn du die drei Vektoren $\vec a$, $\vec b$ und $\vec c$ nebeneinander schreibst.
Wusstest du schon?
Die Determinante kann dir auch in der Informatik begegnen! Sie wird häufig in der Computergrafik verwendet, um Transformationen wie Drehungen und Skalierungen zu berechnen. Wenn du also einmal ein cooles 3D-Spiel spielst, steckt bestimmt irgendwo eine Determinantenberechnung dahinter, die für die richtigen Winkel und Proportionen sorgt!
Gleichungssysteme lösen mit Determinante
Mit Hilfe der Cramerschen Regel kannst du lineare Gleichungssysteme lösen. Dies ist hier am Beispiel eines Gleichungssystems mit zwei Gleichungen und zwei Unbekannten zu sehen.
$\begin{array}{rcrcr} 2x&-&3y&=&7\\ x&+&4y&=&-2 \end{array}$
$~~$
- Zuerst stellst du die Koeffizientenmatrix $A$ dieser Gleichung auf. Diese erhältst du, indem du die Koeffizienten der Unbekannten in einer $2{\times}2$-Matrix aufschreibst. Von dieser Matrix berechnest du die Determinante.
$\quad~~~\text{det}(A)=\begin{vmatrix} 2 & -3 \\ 1 & 4 \end{vmatrix} = 8-({-}3) = 11$
- Zur Berechnung der Lösung für $x$ ersetzt du in der Koeffizientenmatrix die entsprechende, also die erste, Spalte durch die rechte Seite der Gleichung und berechnest von der so erhaltenen Matrix $A_x$ wieder die Determinante.
$\quad~~~\text{det}(A_x) = \begin{vmatrix} 7 & -3 \\ -2 & 4 \end{vmatrix} = 28-6 =22$
- Nun kannst du $x$ berechnen. Du dividierst dazu die berechneten Determinanten.
$\quad~~~x=\dfrac{\text{det}(A_x)}{\text{det}(A)}=\dfrac{22}{11}=2$
- Ebenso kannst du die Lösung für $y$ ermitteln. Dieses Mal ersetzt du in der Koeffizientenmatrix die zweite Spalte ($y$-Spalte) durch die rechte Seite der Gleichung und berechnest die Determinante.
$\quad~~~\text{det}(A_y) = \begin{vmatrix} 2 & 7 \\ 1 & -2 \end{vmatrix} = -11$
- Du erhältst für $y$ als Quotient der Determinanten:
$\quad~~~y=\dfrac{\text{det}(A_y)}{\text{det}(A)}=\dfrac{-11}{11}=-1$
Abhängigkeit von Vektoren prüfen mit Determinante
Eine weitere Anwendung findet die Determinante, wenn du Vektoren auf lineare Unabhängigkeit prüfen möchtest. Sind Vektoren linear abhängig, so ist dies gleichbedeutend damit, dass sich einer der Vektoren als Linearkombination der anderen Vektoren schreiben lässt.
Zur Überprüfung schreibst du die Vektoren nebeneinander in eine Matrix und berechnest die Determinante.
Sind die Vektoren linear abhängig, so ergibt sich für die Determinante der Wert $0$. Umgekehrt weißt du, dass bei einer Ergebnis ungleich $0$ die Vektoren linear unabhängig sind.
Ausblick – das lernst du nach Determinante berechnen
Als nächstes kommen die Themen Cramersche Regel und Inverse Matrizen auf dich zu. Erweitere dein Wissen mit dem Thema Eigenwerten und Eigenvektoren und entdecke wie lineare Abbildungen mit Matrizen zusammenhängen.
Wenn du das Gelernte direkt üben möchtest, kannst du dir den Übungstext zur Determinante angucken.
Zusammenfassung – Determinante
- Die Determinante einer quadratischen Matrix ist eine charakteristische Zahl, die aus den Einträgen der Matrix berechnet werden kann. Mit der Determinante lässt sich unter anderem Aussagen über die Invertierbarkeit von Matrizen treffen.
- Im Allgemeinen lässt sich die Determinante einer $n{\times}n$-Matrix mit dem Laplace'schen Entwicklungssatz berechnen. In den Sonderfällen einer $3{\times}3$-Matrix lässt sich die Regel von Sarrus anwenden:
$$\begin{array}{rccccccc} \begin{array}{|ccc|cc} a & b & c & \color{dodgerblue}{a} & \color{dodgerblue}{b} \\ d & e & f & \color{dodgerblue}{d} & \color{dodgerblue}{e} \\ g & h & i & \color{dodgerblue}{g} & \color{dodgerblue}{h} \end{array} & = && a \cdot e \cdot i &+& b \cdot f \cdot g &+& c \cdot d \cdot h \\ &&-& g \cdot e \cdot c &-& h \cdot f \cdot a &-& i \cdot d \cdot b \end{array}$$
-
Für eine $2{\times}2$-Matrix gilt außerdem:
$$\text{det}\begin{pmatrix} a& b \\ c&d \end{pmatrix}=\begin{vmatrix} a & b \\ c & d \end{vmatrix} = a \cdot d - c \cdot b$$
Mithilfe der Determinante lassen sich im zweidimensionalen Raum auch Flächeninhalte von Parallelogrammen und Dreiecken bestimmen, wenn die Vektoren diese Figur aufspannen und die Matrix als Spaltenvektoren bilden. Gleiches kann im dreidimensionalen Raum angewandt werden, wodurch die Volumenberechnung eines Spats durch die Determinante ermöglicht wird.
Häufig gestellte Fragen zum Thema Determinante
Transkript Determinante berechnen
In diesem Video: Der DeTERMINATOR! Ach, ne. Das Ding hieß "Determinante". Auch nicht schlecht. Schauen wir mal, was es damit auf sich hat. Was könnte sich wohl hinter einem solch bemerkenswerten Fachbegriff verbergen? Nun, im Endeffekt ist es ganz einfach: Eine Zahl. Und zwar eine Zahl, die einer quadratischen Matrix zugeordnet wird. Eine quadratische Matrix ist eine Matrix, die genauso viele Spalten wie Zeilen hat. Also "Zwei-Kreuz-Zwei" , "Drei-Kreuz-Drei" und so weiter. Und diesen Matrizen wird jetzt einfach eine "Zahl" zugeordnet? Das klingt erstmal sehr willkürlich. Wir können eine Determinante aber ganz konkret aus den Einträgen einer gegebenen Matrix berechnen! Wir schauen uns zuerst den einfachsten Fall an und betrachten eine "zwei-Kreuz-zwei"-Matrix. Für die Determinante dieser Matrix gibt es jetzt verschiedene Schreibweisen. Eine Möglichkeit besteht darin, einfach die Abkürzung "det" vor die Matrix zu setzen, eine andere darin, senkrechte Striche um die Matrix zu setzen, die in diesem Kontext nicht mit Betragsstrichen verwechselt werden sollten. Aber egal welche Schreibweise wir wählen, die Rechenvorschrift bleibt die selbe! Wir multiplizieren entlang der Hauptdiagonalen und ziehen anschließend das Produkt der Einträge auf der Nebendiagonalen ab. Bei der Berechnung muss man aufpassen, dass man mit den Vorzeichen nicht durcheinander kommt. Aber dann erhalten wir (wie versprochen) eine ganz konkrete Zahl als Ergebnis. Für eine allgemeine "zwei-Kreuz-zwei"-Matrix mit den Einträgen a, b, c und d lautet die Formel für die Determinante also: Hauptdiagonale, sprich "a mal d", minus Nebendiagonale, sprich "c mal b". Am Besten verinnerlicht man das, wenn man es ein paar mal selber durchrechnet. Hier sind noch zwei Matrizen zur Übung. Pausiere das Video doch kurz und rechne selbst! Wie wir sehen, kann die Determinante auch eine negative Zahl sein. Ob das Ergebnis positiv oder negativ sein wird, lässt sich aber nicht unbedingt direkt an den Einträgen der Matrix ablesen. Etwas aufwendiger wird es, wenn wir die Determinante einer "drei-Kreuz-drei"-Matrix berechnen möchten. Grundsätzlich funktioniert dabei aber die gleiche Vorgehensweise, nur dass wir jetzt einen kleinen Trick anwenden. Um die Determinante leichter berechnen zu können, schreiben wir uns nämlich die ersten beiden Spalten der Matrix nochmal rechts daneben. Dann müssen wir zunächst wieder die Hauptdiagonale betrachten, genauer gesagt: die Hauptdiagonalen. Denn jetzt gibt es nicht nur eine Diagonale von links oben nach rechts unten, sondern drei! Die Produkte dieser drei Diagonalen müssen wir also zunächst addieren. Dann schauen wir auf die Nebendiagonalen. Also die die drei Diagonalen von links unten nach rechts oben. Diese drei Produkte werden jeweils abgezogen. Der Rest ist Fleißarbeit. Wie du siehst, ist der Rechenweg etwas länger. Aber wenn wir uns das Muster gemerkt haben, ist es trotzdem nicht schwer. Es wird übrigens üblicherweise "Regel von Sarrus" genannt. Wenn du magst, kannst du die Vorgehensweise ja mal an dieser Matrix (der sogenannten "Telefonmatrix") trainieren. Bekommst du Null raus, hast du alles richtig gemacht! Glaubst du nicht!? Dann rechne nach! Okay, lass uns nochmal zusammenfassen, was wir uns zur Berechnung von Determinanten merken sollten. Wenn wir eine quadratische Matrix gegeben haben, also eine Matrix, deren Anzahl an Zeilen gleich ihrer Anzahl an Spalten ist, können wir für eine solche Matrix die Determinante berechnen. Für "Zwei-Kreuz-Zwei"- und "Drei-Kreuz-Drei"-Matrizen ist es am einfachsten, die Hauptdiagonalen und Nebendiagonalen zu nutzen. Hier siehst du die entsprechenden Formeln. Bei "Drei-Kreuz-Drei"-Matrizen nennt man die Vorgehensweise auch "Regel von Sarrus". Es kann sich lohnen, die ersten beiden Spalten nochmal rechts neben die Matrix zu schreiben, um den Überblick zu behalten. Klasse, dann bleibt eigentlich nur noch eine Frage: Wozu machen wir den ganzen Quatsch eigentlich? Nun, für manche Rechnungen, wie zum Beispiel auch das Lösen von linearen Gleichungssystemen, kann die Determinante ziemlich nützlich sein und uns Arbeit ersparen. Unter bestimmten Voraussetzungen kann man mit ihr sogar Flächeninhalte und Volumina sehr effizient bestimmen! Wenn du also weißt, wie du die Determinante von Matrizen berechnen kannst, hast du einen mächtigen Verbündeten an deiner Seite!
Determinante berechnen Übung
-
Beschreibe, was man unter einer Determinante versteht.
TippsFür die Determinante der Matrix $A$ gibt es verschiedene Schreibweisen:
$\det (A)$
beziehungsweise:
$\det \begin{pmatrix} a & b \\ c & d \end{pmatrix}$
Wir können die Determinante einer $2{\times}2$-Matrix mit der folgenden Formel berechnen:
$\begin{vmatrix} a & b \\ c & d \end{vmatrix} = a \cdot d - c \cdot b$
Zwei der Aussagen sind falsch.
Lösung- Eine Determinante ist eine Zahl, die einer quadratischen Matrix zugeordnet wird.
Eine quadratische Matrix ist eine Matrix, die genauso viele Spalten wie Zeilen hat, also beispielsweise eine $2{\times}2$- oder eine $3{\times}3$-Matrix.
Für die Determinante der Matrix $A$ gibt es verschiedene Schreibweisen:
$\det (A)$
beziehungsweise:
$\det \begin{pmatrix} a & b \\ c & d \end{pmatrix}$
oder auch:
$|A|$
beziehungsweise:
$\begin{vmatrix} a & b \\ c & d \end{vmatrix}$
Dabei handelt es sich jedoch nicht um die Betragsstriche.
Die Schreibweise $\det |A|$ ist hingegen falsch, somit auch diese Aussage:
- Für die Determinante der Matrix $A$ schreiben wir kurz: $\det |A|$.
Wir können die Determinante einer $2{\times}2$-Matrix mit der folgenden Formel berechnen:
$\begin{vmatrix} a & b \\ c & d \end{vmatrix} = a \cdot d - c \cdot b$
- Zur Berechnung der Determinanten einer $2{\times}2$-Matrix multiplizieren wir entlang der Hauptdiagonalen und ziehen das Produkt der Nebendiagonalen ab.
Wir können die Determinante einer $3{\times}3$-Matrix mithilfe der Regel von Sarrus berechnen:
$\begin{vmatrix} a & b & c \\ d & e & f \\ g & h & i \end{vmatrix} = aei + bfg + cdh - gec - hfa - ibd$
Somit ist folgende Aussage falsch:
- Die Regel von Sarrus bezieht sich auf $4{\times}4$-Matrizen.
-
Bestimme die Determinanten der $2{\times}2$-Matrizen.
TippsAchte auf negative Vorzeichen.
LösungEine Determinante ist eine Zahl, die einer quadratischen Matrix zugeordnet ist.
Für eine $2{\times}2$-Matrix gilt zur Bestimmung der Determinante diese Rechenvorschrift:
$\begin{vmatrix} a & b \\ c & d \end{vmatrix} = a \cdot d - c \cdot b$
Wir berechnen nun die Determinaten der gegebenen Matrizen:
$\begin{vmatrix} 2 & 6 \\ 5 & 7 \end{vmatrix} = 2 \cdot 7 - 5 \cdot 6 = 14 - 30 = -16$
$\begin{vmatrix} -3 & -2 \\ 1 & -4 \end{vmatrix} = -3 \cdot (-4) - 1 \cdot (-2) = 12 + 2 = 14$
$\begin{vmatrix} 2 & 2 \\ 2 & -2 \end{vmatrix} = 2 \cdot (-2) - 2 \cdot 2 = -4-4=-8$
$\begin{vmatrix} 5 & 2 \\ -1 & 8 \end{vmatrix} = 5 \cdot 8 - (-1) \cdot 2 = 40 + 2 = 42$
-
Berechne die Determinanten der $3{\times}3$-Matrizen.
Tipps$\begin{vmatrix} a & b & c \\ d & e & f \\ g & h & i \end{vmatrix} = aei + bfg + cdh - gec - hfa - ibd$
Achte auf negative Vorzeichen.
LösungUm die Determinante einer $3{\times}3$-Matrix zu berechnen, müssen wir eine ganz konkrete Zahl ermitteln. Wir können die Determinante einer $3{\times}3$-Matrix mithilfe der Regel von Sarrus berechnen:
$\begin{vmatrix} a & b & c \\ d & e & f \\ g & h & i \end{vmatrix} = aei + bfg + cdh - gec - hfa - ibd$
Zur Berechnung der Determinante addieren wir die Produkte der Hauptdiagonalen und ziehen die Produkte der Nebendiagonalen ab. Die Haupt- und Nebendiagonalen können wir dabei gut erkennen, wenn wir die ersten beiden Spalten der Matrix noch einmal rechts daneben ergänzen:
$\begin{vmatrix} a & b & c \\ d & e & f \\ g & h & i \end{vmatrix} \begin{matrix} a \\ d \\ g \end{matrix} \quad \begin{matrix} b \\ e \\ h \end{matrix}$
Wir kennen nun die Vorgehensweise und können so die Determinanten der gegebenen Matrizen berechnen:
Matrix 1:
$\begin{array}{ll} \begin{vmatrix} 9 & -2 & 1 \\ 0 & 4 & -5 \\ 5 & 2 & 1 \end{vmatrix} &= 9 \cdot 4 \cdot 1 + (-2) \cdot (-5) \cdot 5 + 1 \cdot 0 \cdot 2 - 5 \cdot 4 \cdot 1 - 2 \cdot (-5) \cdot 9 - 1 \cdot 0 \cdot (-2) \\ &= 36 + 50 + 0 - 20 - (-90) - 0 \\ &= 156 \end{array}$
Matrix 2:
$\begin{array}{ll} \begin{vmatrix} 3 & -5 & 1 \\ 8 & 0 & -1 \\ 10 & 2 & 1 \end{vmatrix} &= 3 \cdot 0 \cdot 1 + (-5) \cdot (-1) \cdot 10 + 1 \cdot 8 \cdot 2 - 10 \cdot 0 \cdot 1 - 2 \cdot (-1) \cdot 3 - 1 \cdot 8 \cdot (-5) \\ &= 0 + 50 + 16 - 0 - (-6) - (-40) \\ &= 112 \end{array}$
Matrix 3:
$\begin{array}{ll} \begin{vmatrix} 0 & -2 & 0 \\ 9 & 4 & -6 \\ 2 & -1 & 3 \end{vmatrix} &= 0 \cdot 4 \cdot 3 + (-2) \cdot (-6) \cdot 2 + 0 \cdot 9 \cdot (-1) - 2 \cdot 4 \cdot 0 - (-1) \cdot (-6) \cdot 0 - 3 \cdot 9 \cdot (-2) \\ &= 0 + 24 + 0 - 0 - (-54) \\ &= 78 \end{array}$
-
Ordne die Matrizen nach der Größe ihrer Determinanten.
TippsUm die Determinante einer $2{\times}2$-Matrix zu berechnen, berechnen wir das Produkt der Hauptdiagonalen und ziehen das Produkt der Nebendiagonalen davon ab:
$\begin{vmatrix} a & b \\ c & d \end{vmatrix} = ad - bc$
Berechne zuerst die Determinanten aller vier Matrizen. Arbeite schriftlich. Anschließend kannst du sortieren.
LösungUm die Determinante einer $2{\times}2$-Matrix zu berechnen, berechnen wir das Produkt der Hauptdiagonalen und ziehen das Produkt der Nebendiagonalen davon ab:
$\begin{vmatrix} a & b \\ c & d \end{vmatrix} = ad - bc$
Wir berechnen jetzt die Determinanten der gegebenen Matrizen und sortieren anschließend:
$\begin{array}{ll} \begin{vmatrix} 1 & 2 \\ 3 & 2 \end{vmatrix} &= 1\cdot 2 - 3\cdot 2 \\ &= 2 - 6\\ &= -4 \end{array}$
$\begin{array}{ll} \begin{vmatrix} 1 & 0 \\ 2 & 2 \end{vmatrix} &= 1\cdot 2 - 2\cdot 0 \\ &= 2 - 0\\ &= 2 \end{array}$
$\begin{array}{ll} \begin{vmatrix} 3 & 1 \\ 1 & 2 \end{vmatrix} &= 3\cdot 2 - 1\cdot 1 \\ &= 6 - 1\\ &= 5 \end{array}$
$\begin{array}{ll} \begin{vmatrix} 3 & 1 \\ -2 & 3 \end{vmatrix} &= 3\cdot 3 - 1\cdot (-2) \\ &= 9 - (-2) = 9+2 \\ &= 11 \end{array}$
Die richtige Reihenfolge lautet also:
$\begin{vmatrix} 1 & 2 \\ 3 & 2 \end{vmatrix} \quad < \quad \begin{vmatrix} 1 & 0 \\ 2 & 2 \end{vmatrix} \quad < \quad \begin{vmatrix} 3 & 1 \\ 1 & 2 \end{vmatrix} \quad < \quad \begin{vmatrix} 3 & 1 \\ -2 & 3 \end{vmatrix}$
-
Gib an, von welchen mathematischen Objekten sich eine Determinante berechnen lässt.
TippsEine Determinante ist eine Zahl, die einer quadratischen Matrix zugeordnet wird.
Du musst zwei Objekte auswählen.
LösungEine Determinante ist eine Zahl, die einer quadratischen Matrix zugeordnet wird.
Eine quadratische Matrix ist eine Matrix, die genauso viele Spalten wie Zeilen hat, also beispielsweise eine $2{\times}2$- oder eine $3{\times}3$-Matrix.Wir betrachten die gegebenen Objekte:
- $\begin{pmatrix} 2 & 3 & 9 \\ 0 & -1 & -10 \\ 10 & 0 & 1 \end{pmatrix}$
$\begin{array}{ll} \begin{vmatrix} 2 & 3 & 9 \\ 0 & -1 & -10 \\ -10 & 0 & 1 \end{vmatrix} &= 2 \cdot (-1) \cdot 1 + 3 \cdot (-10) \cdot (-10) + 9 \cdot 0 \cdot 0 - (-10) \cdot (-1) \cdot 9 - 0 \cdot (-10) \cdot 2 - 1 \cdot 0 \cdot 3 \\ & = -2 + 300 + 0 - 90 - 0 - 0 \\ &= 208 \end{array}$
- $\begin{pmatrix} 3 \\ 5 \\ -1 \end{pmatrix}$
- $\begin{pmatrix}-1 & -1 & 3 \\ 0 & 4 & 2 \end{pmatrix}$
- $\begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}$
$\begin{vmatrix} 1 & 2 \\ 3 & 4 \end{vmatrix} = 1 \cdot 4 - 3 \cdot 2 = 4 - 6 = -2$
- $\begin{pmatrix} 2 & -4 \\ 3 & -10 \\ 0 & 9 \end{pmatrix}$
- $\begin{pmatrix} 2 \\ -2 \end{pmatrix}$
-
Vervollständige die Matrix mit der Zahl $a$ so, dass die Determinante genau $0$ ergibt.
TippsBestimme zunächst die Determinante mithilfe der Regel von Sarrus. Nimm dabei die Variable $a$ wie eine Zahl mit.
Du erhälst:
$2 \cdot a \cdot 10 + 5 \cdot (-10) \cdot 2 + (-2) \cdot 0 \cdot 2 - 2 \cdot a \cdot (-2) - 2 \cdot (-10) \cdot 2 - 10 \cdot 0 \cdot 5$
Vereinfache den Term und setze ihn gleich $0$. Löse ihn dann nach $a$ auf.
LösungWir betrachten die gegebene Matrix:
$\begin{pmatrix} 2 & 5 & -2 \\ 0 & a & -10 \\ 2 & 2 & 10 \end{pmatrix}$
Da es sich um eine $3{\times}3$-Matrix handelt, können wir ihre Determinante mithilfe der Regel von Sarrus berechnen:
$\begin{vmatrix} a & b & c \\ d & e & f \\ g & h & i \end{vmatrix} = aei + bfg + cdh - gec - hfa - ibd$
Wir berechnen nun zunächst die Determinante unter Verwendung der obigen Formel:
$\begin{vmatrix} 2 & 5 & -2 \\ 0 & a & -10 \\ 2 & 2 & 10 \end{vmatrix} = 2 \cdot a \cdot 10 + 5 \cdot (-10) \cdot 2 + (-2) \cdot 0 \cdot 2 - 2 \cdot a \cdot (-2) - 2 \cdot (-10) \cdot 2 - 10 \cdot 0 \cdot 5$
Diesen Term vereinfachen wir zu:
$20a + (-100) + 0 - (-4a) - (-40) - 0 = 20a - 100 + 4a +40 = 24a -60$
Jetzt setzen wir den Term gleich $0$ und lösen nach $a$ auf:
$\begin{array}{lll} 24a - 60 &= 0 &|+60 \\ 24a &= 60 &|:24 \\ a &= 2{,}5 & \\ \end{array}$
Wenn wir für $a=2{,}5$ einsetzen, ist die Determinante der Matrix genau $0$. Die Matrix lautet also:
$\begin{pmatrix} 2 & 5 & -2 \\ 0 & 2{,}5 & -10 \\ 2 & 2 & 10 \end{pmatrix}$
9.713
sofaheld-Level
6.600
vorgefertigte
Vokabeln
7.837
Lernvideos
37.239
Übungen
32.630
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Schulstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung





 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?





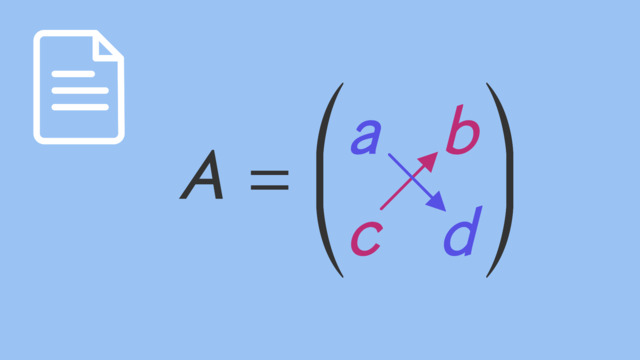









Mathe ist sooo schwierig 😥. Schade, dass man das nicht irgendwann abwählen kann wie Latein 😅
ok
Das ist doch nie im leben 10.klasse ich schwöre ich habe kein wort verstanden was das gelabert wurde
Sehr gut erklärt 👍
Danke😘🥰
Determinator 3000 : )