Cramersche Regel – Beispiele


in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Grundlagen zum Thema Cramersche Regel – Beispiele
In diesem Video wird dir anhand von Beispielen gezeigt, wie du die Cramersche Regel zum Lösen von linearen Gleichungssystemen mit zwei Unbekannten anwenden kannst. Zuerst wiederholen wir gemeinsam die Cramersche Regel und die Berechnung der Determinante einer 2x2-Matrix. Im Anschluss siehst du an zwei Beispielen, wie lineare Gleichungssysteme mit Hilfe der Cramerschen Regel gelöst werden können. Ganz zum Schluss fasse ich noch einmal das Wichtigste für dich zusammen.
Cramersche Regel – Beispiele Übung
-
Bestimme die Lösung für x und y des linearen Gleichungssystems mit der Cramerschen Regel.
TippsUm die Cramersche Regel anwenden zu können, benötigen wir zunächst die Werte der Determinanten.
Die Cramersche Regel lautet:
$x=\frac{det~A_x}{det~A}$
$y=\frac{det~A_y}{det~A}$
Lösung- Zunächst erstellen wir die $2~x~3$ Matrix B:
2. Dann berechnen wir die $det~A$:
$det~A=det \begin{pmatrix} 8 & 9 \\ 11 & 12 \end{pmatrix}=8 \cdot 12 - 11 \cdot 9=96 - 99=-3$
3. Als nächstes berechnen wir die Determinanten $det~A_x$ und $det~A_y$:
$det~A_x= det \begin{pmatrix} 10 & 9 \\ 13 & 12 \end{pmatrix}=10 \cdot 12 - 13 \cdot 9=120 - 117=3$
$det~A_x= det \begin{pmatrix} 8 & 10 \\ 11 & 13 \end{pmatrix}=8 \cdot 13 - 11 \cdot 10=104 - 110=-6$
4. Anschließend setzen wir die Werte in die Cramersche Regel ein:
$x=\frac{det~A_x}{det~A}=\frac{3}{-3}=-1$
$y=\frac{det~A_y}{det~A}=\frac{-6}{-3}=2$
$L=\{(-1;2)\}$
5. Schlussendlich müssen wir noch überprüfen, ob wir richtig gerechnet haben. Wir machen die Probe:
$\begin{align} &\text{I}& 8(-1)+9(2)&=10 \\ &\text{II}& 11(-1)+12(2)&=13 \\ \\ &\text{I}& -8+18&=10 \\ &\text{II}& -11+24&=13 \\ \\ &\text{I}& 10&=10 \\ &\text{II}& 13&=13 \\ \end{align}$
Wir erhalten eine wahre Aussage! Also stimmt die angegebene Lösungsmenge.
-
Berechne die Lösungsmenge für x und y mit der Cramerschen Regel.
TippsUm die Matrix $B$ zu bestimmen, lies einfach die Koeffizienten aus dem linearen Gleichungssystem ab und trage sie der Reihe nach in die Matrix ein.
Den Wert einer Determinante errechnet man durch das Produkt der Hauptdiagonalelemente minus dem Produkt der Nebendiagonalelemente einer quadratischen $2$ x $2$ Matrix.
Lösung- Zunächst erstellen wir die $2~x~3$ Matrix $B$:
2. Dann berechnen wir die $det~A$:
$det~A=det \begin{pmatrix} 3 & 9 \\ 4 & 12 \end{pmatrix}=3 \cdot 9 - 4 \cdot 9=36 - 36=0$
Als Voraussetzung für die Cramersche Regel gilt allerdings, dass die $det~A \neq 0$ sein muss. Was auch Sinn macht, denn wäre die Determinante $A$ gleich $0$, würden wir durch $0$ teilen, was wir aber in der Mathematik niemals machen dürfen.
Das lineare Gleichungssystem hat also keine Lösung.
Demzufolge verlaufen die beiden Geraden parallel zueinander und haben keinen Schnittpunkt.
-
Berechne die Werte der Determinanten.
TippsDie allgemeine Formel zur Berechnung des Wertes einer Determinanten lautet:
$det~A=\begin{vmatrix} a & b \\ c & d \end{vmatrix}=a \cdot d - c \cdot b$
LösungDie allgemeine Formel zur Berechnung des Wertes einer Determinanten lautet:
$det~A=\begin{vmatrix} a & b \\ c & d \end{vmatrix}=a \cdot d - c \cdot b$
Bezogen auf die Aufgaben lassen sich die Determinanten wie folgt bestimmen:
$det \begin{pmatrix} 2 & 2 \\ 2 & 2 \end{pmatrix}=4 - 4=0$
$det \begin{pmatrix} 0 & 4 \\ 2 & 6 \end{pmatrix}=0 - 8=-8$
$det \begin{pmatrix} 4 & 5 \\ 6 & 7 \end{pmatrix}=28 - 30=-2$
$det \begin{pmatrix} -3 & 4 \\ 6 & -2 \end{pmatrix}=6 - 24=-18$
-
Gib an, in welchem Diagramm die Determinante A des zugrunde liegenden linearen Gleichungssystems den Wert „0“ besitzt.
TippsAls Voraussetzung damit wir die Cramersche Regel anwenden können, darf die Determinante A nicht gleich „0“ sein.
Gibt es für das lineare Gleichungssystem keine Lösung, sind die Geraden parallel zueinander.
LösungMit der Cramerschen Regel können wir die Lösungsmenge eines linearen Gleichungssystem mit zwei Unbekannten bestimmen.
Hierzu brauchen wir allerdings die Determinante A. Als Voraussetzung damit wir die Cramersche Regel anwenden können, darf die Determinante A nicht gleich „0“ sein.
Falls doch, gibt es für das lineare Gleichungssystem keine Lösung und die Geraden sind parallel zueinander.
Genau diese Erkenntnis hilft uns bei der Lösung dieser Aufgabe.
- Die Diagramme, die zwei parallele Geraden darstellen, können wir einem Gleichungssystem mit der Determinante $det~A=0$ zuordnen.
- Andersherum können wir die Diagramme, die zwei Geraden mit einem Schnittpunkt, bzw. einem Schnittpunkt außerhalb des Blickfensters, einem Gleichungssystem mit der Determinante $det~A \neq 0$ zuordnen.
-
Gib an, welche Merksätze richtig oder falsch sind.
TippsÜberlege dir, welche Voraussetzung die Cramersche Regel hat.
Den Wert $x$ der Lösungsmenge berechnet man mit Hilfe der Cramerschen Regel wie folgt:
$x=\frac{det~A_x}{det~A}$
Wenn wir den Wert für $det~A$ berechnen und dieser Wert $0$ beträgt, was bedeutet das dann für die Berechnung von $x$?
LösungDie Cramersche Regel lautet:
$x=\frac{det~A_x}{det~A}~~~y=\frac{det~A_y}{det~A}$
Voraussetzung: $det~A \neq 0$
Mit Hilfe von Determinanten können wir also feststellen, ob ein lineares Gleichungssystem eindeutig lösbar ist.
Ist die $det~A \neq 0$, kann man die Lösung für $x$ und $y$ mit der Cramerschen Regel ausrechnen und die Lösung ist eindeutig.
Falls die $det~A=0$, hat das lineare Gleichungssystem keine Lösung. Die Geraden verlaufen parallel zueinander und haben keinen Schnittpunkt.
Mit der Probe kannst du lediglich überprüfen, ob deine Lösungsmenge richtig ist. Du bestimmst mit der Probe allerdings keine Werte für x und y.
Die Cramersche Regel ist nicht die einzige Methode um ein lineares Gleichungssystem zu lösen. Neben der Cramerschen Regel gibt es noch das Additions-, Gleichsetzungs- und Einsetzungsverfahren, sowie graphisches Lösen.
-
Berechne den Schnittpunkt zweier Geraden mit der Cramerschen Regel.
Tipps$f(x)$ bzw. $g(x)$ steht in linearen Funktionen für $y$.
Zunächst müssen wir die beiden Geraden in ein lineares Gleichungssystem schreiben. Wir achten darauf, dass die Variablen x und y auf der einen Seite und der Wert der Konstanten auf der anderen Seite der Gleichung stehen.
Um die linearen Funktionen in ein lineares Gleichungssystem umzuformen, ersetzt man zunächst $f(x)$ und $g(x)$ durch y und stellt die Gleichungen so um, dass $x$ und $y$ auf der linken Seite der Gleichung stehen.
Ein Beispiel:
$\begin{array}{rcll} f(x) &=& 2\cdot x + 1 & \vert& f(x) \text{ durch } y \text{ ersetzen}\\ y &=& 2\cdot x + 1 & \vert& -2\cdot x\\ -2\cdot x + y &=& 1 & \vert& \cdot (-1)\\ 2\cdot x - y &=& -1 \end{array}$
Die Lösungsmenge für x und y sind die Koordinaten des Schnittpunktes $S(x\vert y)$.
LösungWir haben zwei Geraden gegeben:
$y=2x+1$
$y=3x$
Daraus können wir zunächst ein lineares Gleichungssystem bestimmen: (Achte hierbei darauf, dass die Variablen x und y auf der einen Seite und der Wert der Konstante auf der anderen Seite des Gleichung stehen.)
$\begin{align} &\text{I}& 2x-1y&=-1 \\ &\text{II}& 3x-1y&=0 \\ \end{align}$
Wir wollen nun mit der Cramerschen Regel die Lösungsmenge $L=\{(x;y)\}$ bestimmen. Hierzu erstellen wir zunächst die Matrix B:
$B= \begin{pmatrix} 2 & -1 & -1 \\ 3 & -1 & 0 \end{pmatrix}$
Nun bestimmen wir die Determinanten:
$det~A=det \begin{pmatrix} 2 & -1 \\ 3 & -1 \end{pmatrix}=2 \cdot (-1) - 3 \cdot (-1)=-2 - (-3)=1$
$det~A_x=det \begin{pmatrix} -1 & -1 \\ 0 & -1 \end{pmatrix}=-1 \cdot (-1) - 0 \cdot (-1)=1$
$det~A_y=det \begin{pmatrix} 2 & -1 \\ 3 & 0 \end{pmatrix}=2 \cdot 0 - 3 \cdot (-1)=0 - (-3)=3$
Jetzt müssen wir nur noch unsere Werte in die Cramersche Regel einsetzen und wir erhalten die x und y Koordinaten des Schnittpunktes beider Geraden.
$x=\frac{1}{1}=1$
$y=\frac{3}{1}=3$
Somit lautet der Schnittpunkt $S(1|3)$.
9.819
sofaheld-Level
6.600
vorgefertigte
Vokabeln
7.800
Lernvideos
37.183
Übungen
32.618
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Schulstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung




 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?



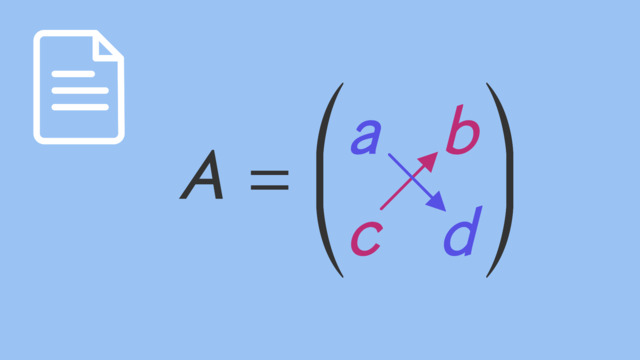









Hi
;-)
Einfach :-) Dankeschön fürs tolle Erklärung
ach kann das Leben einfach sein:-) Danke für die tolle Erläuterung!