Flächenberechnungen bei Kurvendiskussionen
Wie groß ist die Flächen zwischen einem Funktionsgraphen und der x-Achse oder einem zweiten Funktionsgraphen?
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Flächenberechnung
- Der Hauptsatz der Differential- und Integralrechnung
- Das unbestimmte Integral
- Rechenregeln für Integrale
- Das bestimmte Integral
Flächenberechnung
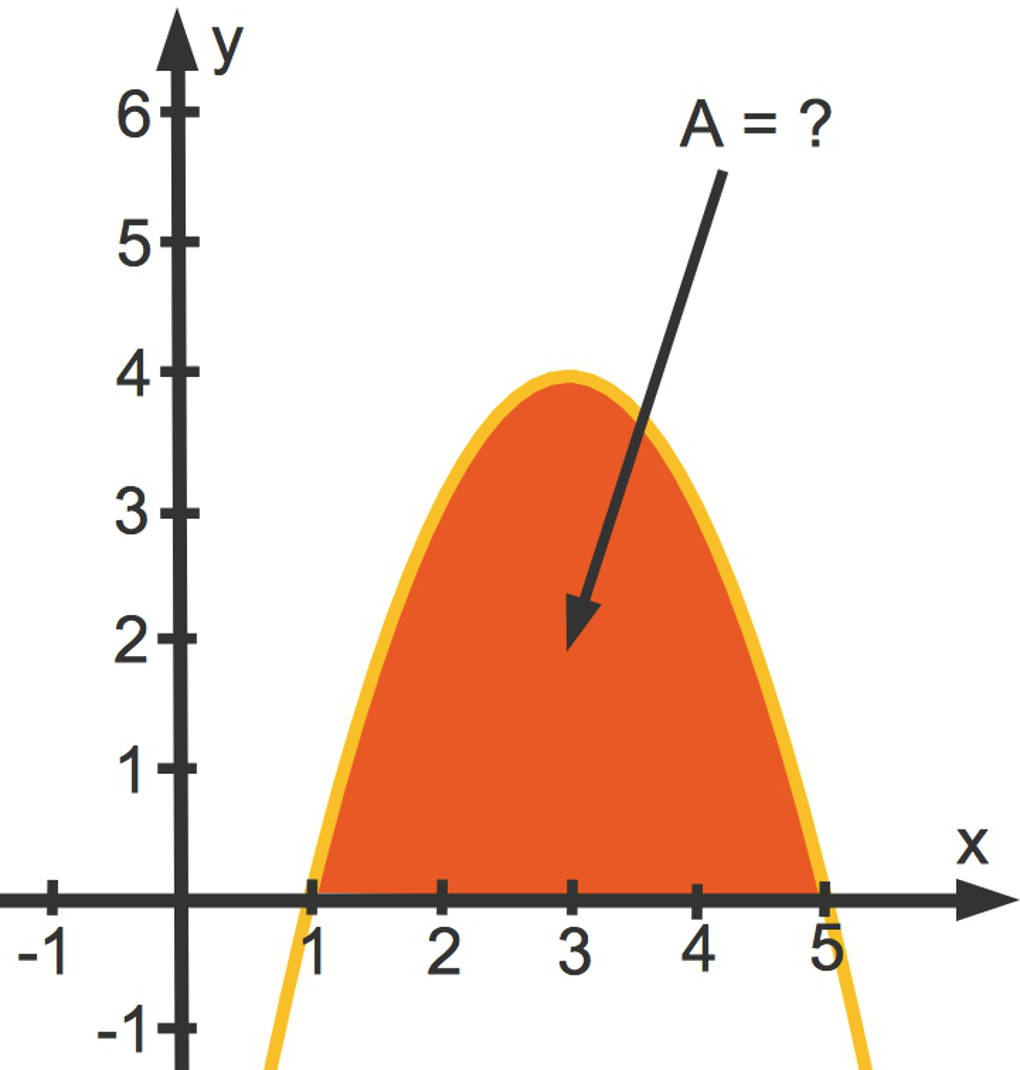
Eine wichtige Anwendung der Integralrechnung ist die Flächenberechnung. Dabei wird der Inhalt von Flächenstücken berechnet, welche entweder von einem Funktionsgraphen und der x-Achse eingeschlossen werden (siehe erste Abbildung)
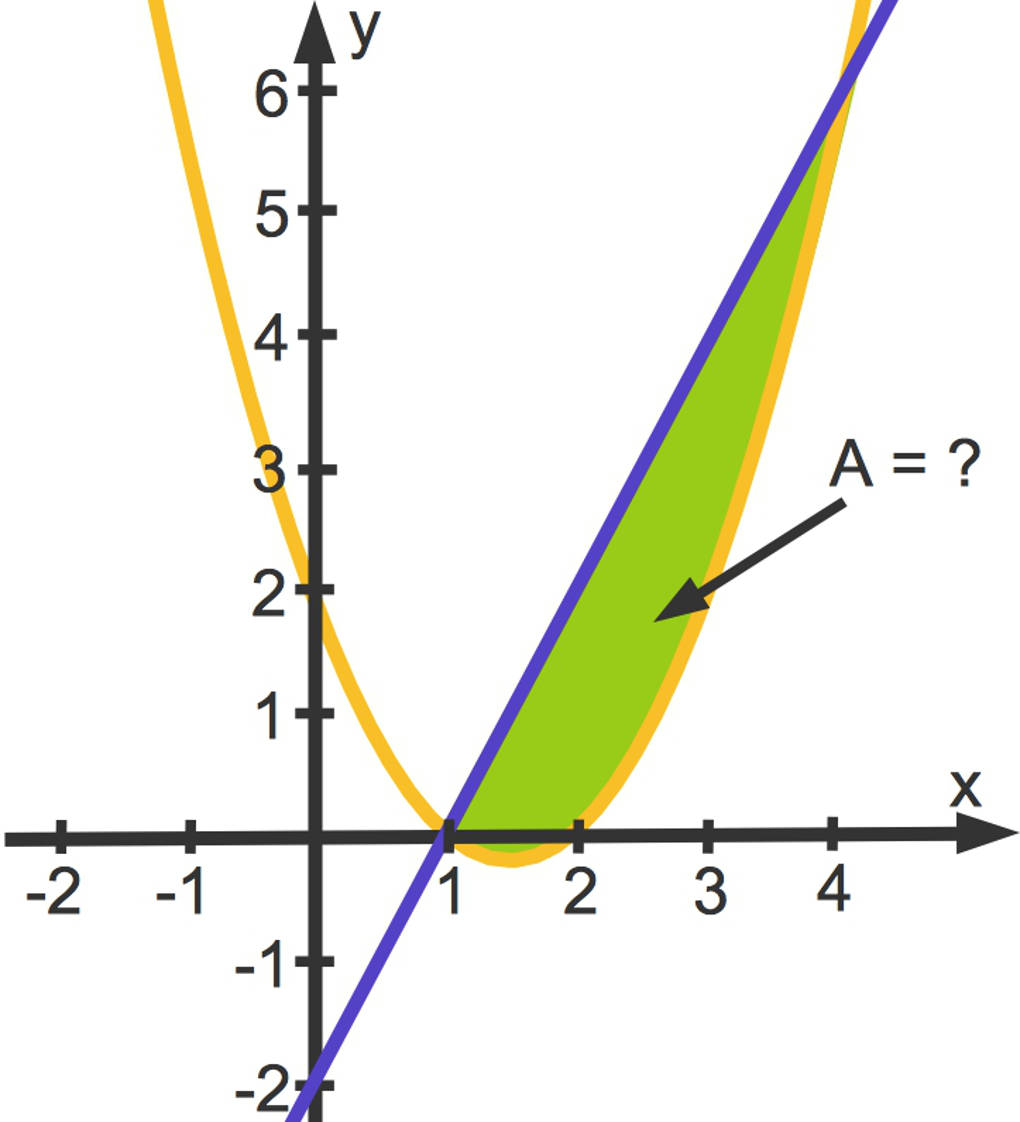
oder welche zwischen zwei Funktionsgraphen liegen (siehe zweite Abbildung).
In beiden Fällen benötigen wir den Hauptsatz der Differential- und Integralrechnung.
Der Hauptsatz der Differential- und Integralrechnung
Das unbestimmte Integral
Jede Funktion $F(x)$, deren Ableitung $F'(x)=f(x)$ ist, heißt Stammfunktion von $f(x)$. Die Menge aller Stammfunktionen wird als unbestimmtes Integral $\int~f(x)~dx$ bezeichnet.
Dabei ist
- $\int$ das Integrationszeichen,
- $f(x)$ die zu integrierende Funktion und
- $dx$ zeigt die Integrationsvariable $x$ an.
Das unbestimmte Integral einer Funktion $f(x)$ ist somit selbst wieder eine Funktion oder eine Menge von Funktionen (Es ist eine Menge von Funktionen, weil es unendlich viele Konstanten $C$ gibt, die wir zu $F(x)$ addieren können, sodass die Ableitung wieder $f(x)$ ist; $C$ fällt als Konstante nämlich immer weg).
Rechenregeln für Integrale
Auch in der Integralrechnung gibt es wichtige Rechenregeln, die wir verwenden wollen.
- Potenzregel: $\int~x^n~dx=\frac1{n+1}x^{n+1}+C;~n\neq-1$
- Faktorregel: $\int~(k\cdot f(x))~dx=k\cdot \int~f(x)~dx$
- Summenregel: $\int~(f(x)+g(x))~dx=\int~f(x)~dx+\int~g(x)~dx$
Das bestimmte Integral
Das bestimmte Integral hat im Unterschied zum unbestimmten Integral eine untere Integrationsgrenze $a$ sowie eine obere Integrationsgrenze $b$:
$\int\limits_a^b~f(x)~dx$.
Der Hauptsatz der Differential- und Integralrechnung besagt, dass sich das bestimmte Integral der Funktion $f(x)$ in den Grenzen von $a$ bis $b$ wie folgt berechnen lässt:
$\int\limits_a^b~f(x)~dx=[F(x)]_a^b=F(b)-F(a)$.
Dabei ist $F(x)$ eine Stammfunktion von $f(x)$.
Bei der Berechnung des bestimmten Intervalls gehen wir wie folgt vor:
- Stammfunktion $F(x)$ von $f(x)$ berechnen
- Differenz von $F(x)$ an der oberen Integrationsgrenze und $F(x)$ an der unteren Integrationsgrenze berechnen
Das bestimmte Integral ist, sofern die Integrationsgrenzen feste Zahlen sind, ein Wert. Dieser wird auch als Flächenbilanz bezeichnet.
Flächen zwischen einem Funktionsgraphen und der x-Achse
Flächen oberhalb der x-Achse
Wir wollen uns zunächst eine Fläche ansehen, die oberhalb der x-Achse liegt.
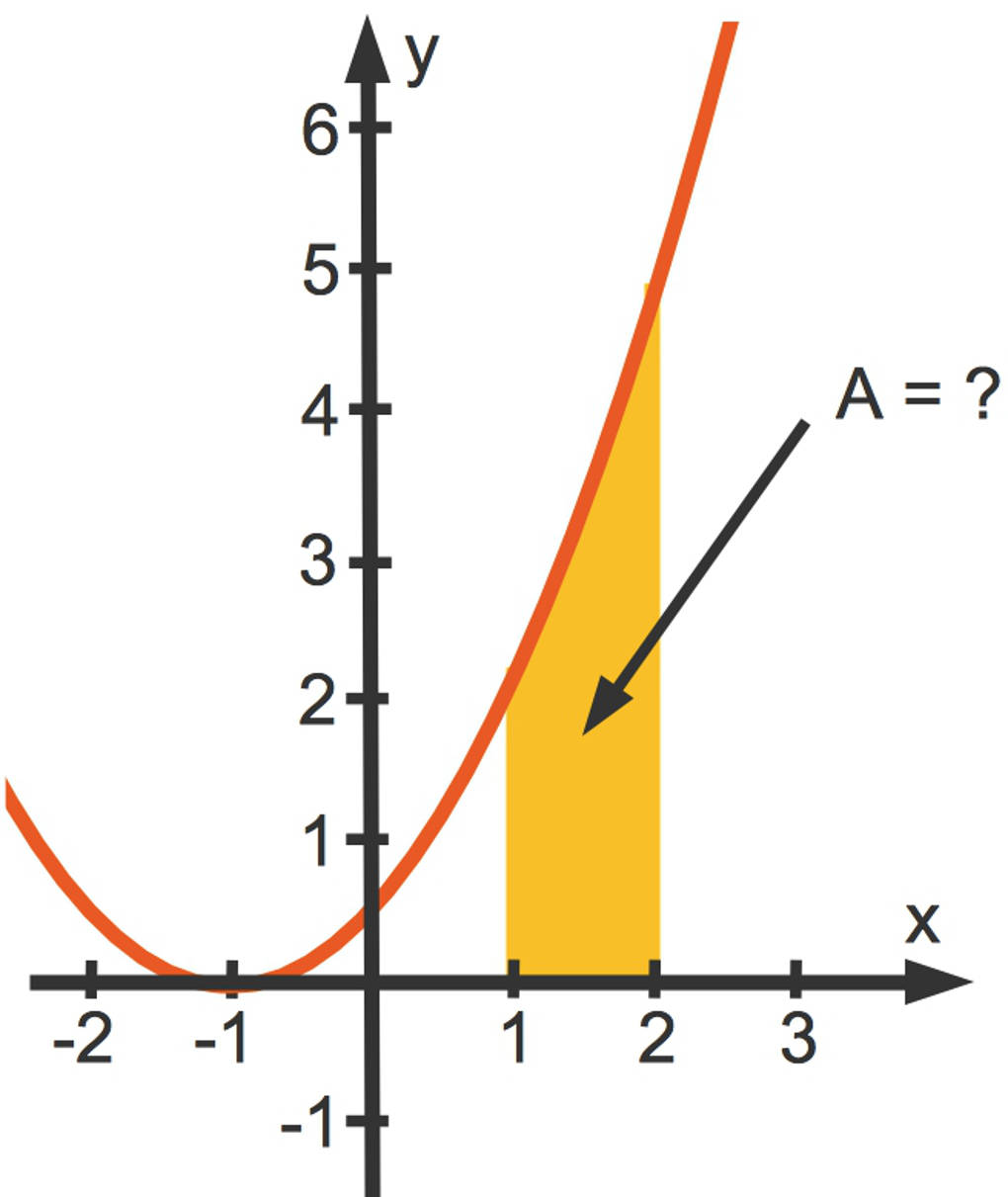
Der Graph der Funktion lautet:
$f(x)=\frac12x^2+x+\frac12$.
Es soll das gelbe Flächenstück unter dem Funktionsgraphen von $f(x)$ über dem Intervall $[1;2]$ berechnet werden. Das bestimmte Integral
$\int\limits_1^2~\left(\frac12x^2+x+\frac12\right)~dx$
gibt den Inhalt dieses Flächenstücks an. Um den Hauptsatz der Differential- und Integralrechnung anzuwenden, musst du zunächst eine Stammfunktion $F(x)$ von $f(x)$ bestimmen. Eine solche ist mit den Rechenregeln der Integration gegeben durch
$F(x)=\frac16x^3+\frac12x^2+\frac12x$.
Wir können die Konstante $C$ am Ende weglassen, da diese bei der folgenden Differenz sowieso wegfällt. Damit ist
$\begin{array}{rcl}A&=&\int\limits_1^2~\left(\frac12x^2+x+\frac12\right)~dx\\ &=&\left[\frac16x^3+\frac12x^2+\frac12x\right]_1^2\\ &=&\left(\frac16 \cdot 2^3+\frac12 \cdot 2^2+\frac12 \cdot 2\right)-\left(\frac16 \cdot 1^3+\frac12 \cdot 1^2+\frac12 \cdot 1\right)\\ &=&\frac{19}6=3,1\bar6~\text{[FE]} \end{array}$.
Natürliche Intervallgrenzen
Die Integrationsgrenzen müssen nicht immer in Form von Intervallgrenzen vorgegeben sein. Hierfür schauen wir uns ein weiteres Beispiel an. Hier siehst du den Graphen der Funktion $f(x)=-x^2+6x-5$.

Die Grenzen des roten Flächenstücks sind die Nullstellen der Funktion. Wir wollen die Nullstellen mithilfe der p-q-Formel bestimmen und multiplizieren dafür die Gleichung $-x^2+6x-5=0$ zunächst mit $-1$. Dann können wir $p=-6$ und $q=5$ entsprechend einsetzen.
$\begin{array}{rcl} x_{1,2}&=&-\frac{-6}2\pm\sqrt{\left(\frac{-6}2\right)^2-5}\\ &=&3\pm\sqrt{4}\\ x_1&=&3+2=5\\ x_2&=&3-2=1 \end{array}$.
Nun kann der Flächeninhalt wieder mit dem Hauptsatz der Differential- und Integralrechnung berechnet werden.
$\begin{array}{rcl}A&=&\int\limits_1^5~\left(-x^2+6x-5\right)~dx\\ &=&\left[-\frac13x^3+3x^2-5x\right]_1^5\\ &=&\left(-\frac13 \cdot 5^3+3\cdot5^2-5\cdot 5\right)-\left(-\frac13 \cdot 1^3+3\cdot1^2-5\cdot 1\right)\\ &=&\frac{32}3=10,\bar6~\text{[FE]} \end{array}$.
Flächen unterhalb der x-Achse
Was passiert, wenn wir den Graphen der Funktion $f(x)$ an der x-Achse spiegeln und das Flächenstück unterhalb der x-Achse liegt? Das bestimmte Integral ist dann negativ.
$\begin{array}{rcl}\int\limits_1^5~\left(x^2-6x+5\right)~dx&=&\left[\frac13x^3-3x^2+5x\right]_1^5\\ &=&\left(\frac13 \cdot 5^3-3\cdot5^2+5\cdot 5\right)-\left(\frac13 \cdot 1^3-3\cdot1^2+5\cdot 1\right)\\ &=&-\frac{32}3=-10,\bar6 \end{array}$.
Ein negativer Flächeninhalt ist nicht definiert. Wir rechnen in solchen Fällen mit Betragsstrichen, um auf jeden Fall ein positives Ergebnis zu erhalten.
$A=\left|-10,\bar6\right|=10,\bar6~\text{[FE]}$
Im Rahmen einer Kurvendiskussion wird der Graph der Funktion $f(x)$ gezeichnet und du kannst erkennen, ob das Flächenstück oberhalb oder unterhalb der x-Achse liegt. Sollte der Funktionsgraphen nicht vorliegen, kannst du immer mit Beträgen rechnen. Das Ergebnis ist dann immer positiv:
$A=\left|\int\limits_a^b~f(x)~dx\right|$.
Flächen zwischen Funktionsgraphen
Allgemeines Vorgehen
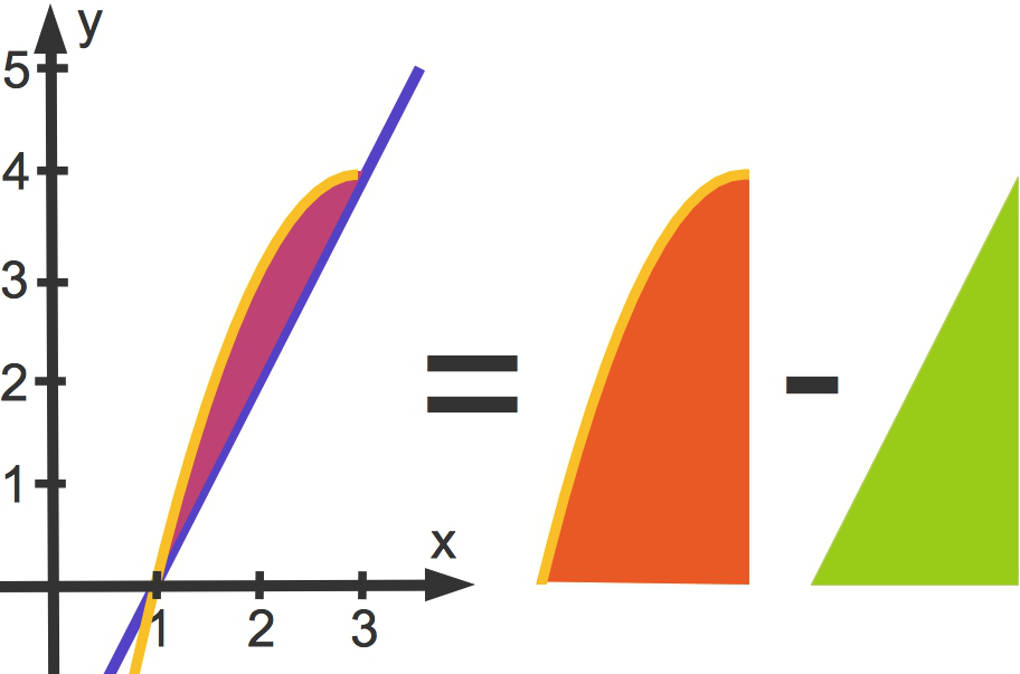
Manchmal liegen die zu berechnenden Flächen zwischen Funktionsgraphen. Wir können den Flächeninhalt trotzdem bestimmen. Es wird einfach das Flächenstück, welches unter der unteren Funktion $g(x)$ liegt, von dem Flächenstück, welches unter der oberen Funktion $f(x)$ liegt, abgezogen. Es ergibt sich somit in den Grenzen von $a$ bis $b$:
$A=\int\limits_a^b~f(x)~dx-\int\limits_a^b~g(x)~dx=\int\limits_a^b~(f(x)-g(x))~dx$.
Wir berechnen also das bestimmte Integral der Differenzfunktion $f(x)-g(x)$.
Beispiel
Schauen wir uns ein Beispiel an. Hier siehst die Graphen der Funktionen $g(x)=2x-2$ sowie $f(x)=x^2-3x+2$.

Die Graphen der beiden Funktionen schließen ein Flächenstück ein. Die Grenzen dieses Flächenstücks sind die Schnittstellen der beiden Funktionen. Diese musst du zunächst bestimmen. Setze hierfür die beiden Funktionen gleich und forme die Gleichung um.
$\begin{array}{llllll} &~& f(x) &=& g(x) &~\\ &\Leftrightarrow& x^2-3x+2 &=& 2x-2 &| -2x+2\\ &\Leftrightarrow& x^2-5x+4 &=& 0 &~ \end{array}$
Dies ist eine quadratische Gleichung, deren Lösung du mit der p-q-Formel erhältst.
$\begin{array}{rcl} x_{1,2}&=&-\frac{-5}2\pm\sqrt{\left(\frac{-5}2\right)^2-4}\\ &=&2,5\pm\sqrt{2,25}\\ x_1&=&2,5+1,5=4\\ x_2&=&2,5-1,5=1 \end{array}$.
An dem Bild kannst du erkennen, dass die Gerade oberhalb der Parabel liegt. Du bildest nun die Differenzfunktion:
$g(x)-f(x)=2x-2-(x^2-3x+2)=-x^2+5x-4$.
Nun kannst du das Flächenstück als bestimmtes Integral dieser Differenzfunktion in den Grenzen von $1$ bis $4$ berechnen.
$\begin{array}{rcl}A&=&\int\limits_1^4~\left(-x^2+5x-4\right)~dx\\ &=&\left[-\frac13x^3+\frac52x^2-4x\right]_1^4\\ &=&\left(-\frac13 \cdot 4^3+\frac52 \cdot 4^2-4\cdot 4\right)-\left(-\frac13 \cdot 1^3+\frac52 \cdot 1^2-4\cdot 1\right)\\ &=&\frac{9}2=4,5~\text{[FE]} \end{array}$
Wenn du nicht weißt, welche der beiden Funktionen oberhalb und unterhalb liegt, kannst du auch hier mit Beträgen rechnen, ohne dass sich das Ergebnis ändert:
$A=\left|\int\limits_a^b~(f(x)-g(x))~dx\right|$.
Alle Videos zum Thema
Videos zum Thema
Flächenberechnungen bei Kurvendiskussionen (2 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Flächenberechnungen bei Kurvendiskussionen (2 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung




 Flächen unter Funktionsgraphen
Flächen unter Funktionsgraphen
 Flächen zwischen Funktionsgraphen
Flächen zwischen Funktionsgraphen









