Bestimmte Integrale und Flächeninhalte


in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Grundlagen zum Thema Bestimmte Integrale und Flächeninhalte
Nach dem Schauen dieses Videos wirst du in der Lage sein, Flächeninhalte, die von der X-Achse und einem Funktionsgraphen eingeschlossen werden, mit Hilfe des bestimmten Integrals zu berechnen.
Zunächst lernst du, wie du das bestimmte Integral berechnest. Anschließend erfährst du, wie sich das bestimmte Integral von dem gesuchten Flächeninhalt unterscheiden kann. Abschließend erfährst du, welche Rechenschritte du beachten musst, um sicherzugehen, dass du den eingeschlossenen Flächeninhalt berechnet hast.

Das Video beinhaltet Schlüsselbegriffe, Bezeichnungen und Fachbegriffe wie bestimmtes Integral, Hauptsatz der Differential- und Integralrechnung, Stammfunktion, Integrationsgrenzen und Flächenbilanz (orientierter Flächeninhalt).
Bevor du dieses Video schaust, solltest du bereits das bestimmte Integral kennen. Außerdem solltest du grundlegendes Wissen zur Integralrechnung haben.
Nach diesem Video wirst du darauf vorbereitet sein, zu lernen, wie man das Volumen von Rotationskörpern berechnen kann.
Bestimmte Integrale und Flächeninhalte Übung
-
Gib den Weg zur Berechnung eines bestimmten Integrals wieder.
TippsNur eine Antwort ist richtig.
Damit wir verstehen, wie bestimmte Integrale im Allgemeinen ausgerechnet werden, schauen wir uns ein kleines Beispiel an:
$\displaystyle \int\limits_0^1 3x^2 \ dx = \bigg[ x^3 \bigg]_0^1 = 1^3 - 0^3 = 1 \ [FE]$
Kannst du in diesem Beispiel identifizieren, was $x^3$ ist?
LösungDas bestimmte Integral $\int\limits_a^b f(x) dx$ berechnen wir mithilfe des Hauptsatzes der Differential- und Integralrechnung. Dieser lautet:
$ \displaystyle \int\limits_a^b f(x) dx = \big[F(x)\big]_a^b = F(b) - F(a)$Beim Anwenden des Hauptsatzes bestimmen wir eine Stammfunktion $F$ zur Funktion $f$ des Integrals. Das bedeutet, dass die Ableitung von der Funktion $F$ wieder die Funktion $f$ selbst ist. Daraufhin setzen wir die Grenzen $a$ und $b$ in die Stammfunktion $F$ ein und subtrahieren.
Beispielweise berechnen wir das bestimmte Integral $\int\limits_0^1 2x \ dx$, indem wir eine Stammfunktion $F$ zur Funktion $f(x) = 2x$ finden. Eine Stammfunktion von $f$ ist $F(x) = x^2$, da ihre Ableitung wieder $f(x) = 2x$ ist. Insgesamt erhalten wir mit dem Hauptsatz:
$\displaystyle \int \limits_0^1 2x \ dx = \big[ x^2 \big]_0^1 = 1^2 - 0^2 = 1 \ [FE] $
-
Vervollständige den Text zu orientierten Flächeninhalten.
TippsBei diesem Beispiel ist das Ergebnis des bestimmten Integrals eine positive Zahl. Das liegt daran, dass sich die eingeschlossene Fläche über der $x$-Achse befindet.
Wenn es mehr Teilflächen gibt, die sich unterhalb der $x$-Achse befinden, dann wissen wir, dass das bestimmte Integral eine negative Zahl ist.
Wenn wir die Teilflächen ausrechnen wollen, dann müssen wir das bestimmte Integral in Teilintegrale mit den passenden Grenzen unterteilen. Die passenden Grenzen sind die Stellen, wo die Funktion die $x$-Achse schneidet.
LösungDas bestimmte Integral $\int\limits_a^b f(x) \ dx$ beschreibt im Intervall $[a,b]$ die Fläche, die von der Funktion $f$ und der $x$-Achse eingeschlossen wird. Gibt es im Intervall $[a,b]$ Nullstellen der Funktion $f$, dann wird die eingeschlossene Fläche in positiv und negativ orientierte Teilflächen eingeteilt. Das bestimmte Integral $\int\limits_a^b f(x) \ dx$ stellt in diesem Fall eine Flächenbilanz über das Intervall $[a,b]$ dar. Wenn es mehr Flächen unterhalb der $x$-Achse als oberhalb gibt, dann bekommen wir für die Flächenbilanz und auch für das bestimmte Integral eine negative Zahl raus. Wir können aber den Gesamtflächeninhalt berechnen, indem wir die orientierten Flächen einzeln berechnen und die Beträge dieser Flächen addieren.
Das Vorgehen, um den Gesamtflächeninhalt zu berechnen, lässt sich in drei Schritte unterteilen:
1) Nullstellen bestimmen.
2) Integral in Teilintegrale zerlegen.
3) Beträge der Teilintegrale addieren .Für das konkrete Beispiel aus dem Bild ergibt sich mit den Nullstellen $x_0 = 0$ und $x_1 = 1$ dann:
$\displaystyle \bigg| \int\limits_{-1}^2 \frac{1}{2}x^3 - 2x^2 + \frac{3}{2}x \ dx \bigg| \\ = \bigg| \int\limits_{-1}^0 \frac{1}{2}x^3 - 2x^2 + \frac{3}{2}x \ dx \bigg| + \bigg| \int\limits_0^1 \frac{1}{2}x^3 - 2x^2 + \frac{3}{2}x \ dx \bigg| + \bigg| \int\limits_1^2 \frac{1}{2}x^3 - 2x^2 + \frac{3}{2}x \ dx \bigg| \\ = \bigg| - \frac{37}{24} \bigg| +\bigg| \frac{5}{24}\bigg| + \bigg| - \frac{13}{24} \bigg| = \frac{55}{24} = 2\frac{7}{24} \ [FE]$
-
Beschreibe die Berechnung des Gesamtflächeninhaltes.
TippsUm den Gesamtflächeninhalt auszurechnen, bestimmen wir die Flächen, die unterschiedlich orientiert sind, einzeln.
Wir können von einer negativ orientierten Fläche den Betrag nehmen, um den Flächeninhalt dieser Fläche zu bestimmen.
Addieren wir die Beträge aller Teilflächen, dann erhalten wir den Flächeninhalt aller eingeschlossenen Flächen zwischen der Funktion und der $x$-Achse.
LösungWenn eine Funktion mit der $x$-Achse sowohl positiv als auch negativ orientierte Flächen einschließt, dann beschreibt das bestimmte Integral die Flächenbilanz. Das bedeutet, wir bekommen nicht den reinen Flächeninhalt raus, denn die negativ orientierten Flächeninhalte werden von den positiv orientierten Flächeninhalten subtrahiert. Möchten wir den Gesamtflächeninhalt ausrechnen, dann gehen wir so vor:
- Nullstellen bestimmen.
- Integral in Teilintegrale zerlegen.
- Beträge der Teilintegrale addieren.
$\displaystyle A = \bigg| \int\limits_a^{x_1} f(x) \ dx \bigg| + \bigg| \int\limits_{x_1}^{x_2} f(x) \ dx \bigg| + \bigg| \int\limits_{x_2}^b f(x) \ dx \bigg|$
Dabei müssen wir beachten, dass die Nullstellen auch die Grenzen des Integrals sein können. Dann gucken wir uns die Nullstellen zwischen diesen beiden Nullstellen an und unterteilen das Integral anhand dieser Nullstellen.
Die richtige Reihenfolge der Rechnung zur Bestimmung des Gesamtflächeninhalts lautet bei der Aufgabe:
1) Wir können anhand des Graphen erkennen, dass die $x$-Werte $x_0 = -1$, $x_1 = 0$ und $x_2=2$ Nullstellen der Funktion sind.
2) Wir unterteilen das Integral nach den Nullstellen im Intervall in Teilintegrale:
$\displaystyle\int\limits_{-1}^2 x^3-x^2-2x \ dx =\int\limits_{-1}^0 x^3-x^2-2x \ dx + \int\limits_0^2 x^3-x^2-2x \ dx $
3) Wir berechnen die Teilintegrale:
$\displaystyle\int\limits_{-1}^0 x^3-x^2-2x \ dx = \frac{5}{12} \ , \ \int\limits_0^2 x^3-x^2-2x \ dx = - \frac{8}{3}$
4) Wir addieren die Beträge der Teilintegrale, um den Betrag der Gesamtfläche zu berechnen:
$\displaystyle \bigg| \int\limits_{-1}^2 x^3-x^2-2x \ dx \bigg| = \bigg| \frac{5}{12} \bigg| + \bigg| -\frac{8}{3} \bigg| = \frac{37}{12} = 3 \frac{1}{12} \ [FE]$
-
Bestimme den gesamten Flächeninhalt der Fläche, der von der Funktion und der x-Achse eingeschlossen wird.
TippsDie inneren Nullstellen sind die Nullstellen, die die Fläche in unterschiedlich orientierte Teilflächen unterteilt.
Wir können die Teilintegrale mithilfe des Hauptsatzes der Differential- und Integralrechnung ausrechnen:
$\displaystyle \int\limits_a^b f(x) \ dx = \bigg[ F(x) \bigg]_a^b = F(b) - F(a) $
Die Funktion $F$ steht für eine Stammfunktion der Funktion $f$.
Der Ausdruck $F(b)$ beschreibt den Funktionswert der Stammfunktion, wenn $b$ in die Funktion eingesetzt wird.
Beispiel: Für die Stammfunktion $F(x)= \dfrac{1}{5} x^5 - \dfrac{5}{3} x^3 + 4x$ ergibt sich der folgende Funktionswert:
$F(1) = \dfrac{1}{5} \cdot 1^5 - \dfrac{5}{3} \cdot 1^3 + 4\cdot 1 = \dfrac{38}{15}$
LösungDas Bestimmen des Gesamtflächeninhaltes lässt sich im Allgemeinen in drei Schritten beschreiben:
1) Intervall an den Nullstellen unterteilen.
2) Integral in Teilintegrale unterteilen.
3) Beträge der Teilintegrale addieren.Wenden wir diese Schritte konkret bei diesem Integral an, dann ergibt sich:
1) Zunächst können wir anhand des Graphen oder rechnerisch feststellen, dass die Nullstellen von der Funktion $f$ die Werte $x_0 = -2$, $x_1 = -1$, $x_2 = 1$ und $x_3 = 2$ sind. Dabei sind die beiden Grenzen des bestimmten Integrals $a=x_0= -2$ und $b=x_3= 2$ zwei dieser Nullstellen. Das bedeutet, zwischen diesen beiden Nullstellen finden wir nur noch die Nullstellen $x_1 =-1$ und $x_2=1$.
2) Mit den beiden Nullstellen im Inneren des Intervalls lässt sich das Integral in drei Teilintegrale zerlegen:
$\displaystyle \int\limits_{-2}^2 x^4 - 5x^2 + 4 \ dx = \int\limits_{-2}^{-1} x^4 - 5x^2 + 4 \ dx + \int\limits_{-1}^{1} x^4 - 5x^2 + 4 \ dx + \int\limits_1^2 x^4 - 5x^2 + 4 \ dx $
Diese Teilintegrale rechnen wir zuerst einzeln aus:
$\displaystyle \int\limits_{-2}^{-1} x^4 - 5x^2 + 4 \ dx = \bigg[ \frac{1}{5}x^5 - \frac{5}{3}x^3 + 4x \bigg]_{-2}^{-1} =\bigg(- \frac{38}{15}\bigg) - \bigg(-\frac{16}{15}\bigg) = - \frac{22}{15}$
$\displaystyle \int\limits_{-1}^{1} x^4 - 5x^2 + 4 \ dx = \bigg[ \frac{1}{5}x^5 - \frac{5}{3}x^3 + 4x \bigg]_{-1}^{1} = \frac{38}{15} - \bigg(- \frac{38}{15}\bigg)=\frac{76}{15}$
$\displaystyle \int\limits_{1}^{2} x^4 - 5x^2 + 4 \ dx = \bigg[ \frac{1}{5}x^5 - \frac{5}{3}x^3 + 4x \bigg]_{1}^{2} = \frac{16}{15} - \frac{38}{15} =- \frac{22}{15}$
3) Zum Schluss addieren wir die Beträge der Teilintegrale, um den gesamten Flächeninhalt auszurechnen. Insgesamt erhalten wir:
$\displaystyle \bigg| \int\limits_{-2}^2 x^4 - 5x^2 + 4 \ dx \bigg| = \bigg| - \frac{22}{15} \bigg| + \bigg| \frac{76}{15} \bigg| + \bigg| -\frac{22}{15} \bigg| = \frac{120}{15} = 8 \ [FE] $
-
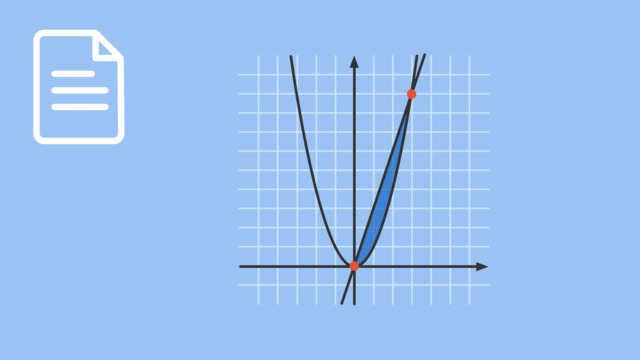
Berechne den eingefärbten Flächeninhalt mithilfe des bestimmten Integrals.
TippsHier musst du den Hauptsatz der Differential- und Integralrechnung anwenden.
Der Hauptsatz der Differential- und Integralrechnung lautet:
$ \displaystyle \int\limits_a^b f(x) dx = \big[F(x)\big]_a^b = F(b) - F(a) $
Die Funktion $F$ ist eine Stammfunktion der Funktion $f$. Das bedeutet, dass $f$ die Ableitung von $F$ ist.
Beispielsweise können wir für die Funktion $f(x) = x$ eine Stammfunktion $F(x) = \dfrac{1}{2} x^2$ finden, da die Ableitung von $F$ wieder $f$ ist:
$ F'(x) = \bigg(\dfrac{1}{2} x^2\bigg)' = x = f(x)$
LösungUm das bestimmte Integral im Intervall $[a,b]$ auszurechnen, wird der Hauptsatz der Differential- und Integralrechnung verwendet. Der Hauptsatz lautet:
$\displaystyle \int\limits_a^b f(x) dx = [F(x)]_a^b = F(b) - F(a) $
Dabei steht die Funktion $F$ für eine Stammfunktion von der Funktion $f$. Das bedeutet, dass $f$ die Ableitung von $F$ darstellt. In diese Stammfunktion werden die Grenzen $a$ und $b$ eingesetzt und die Differenz der beiden Funktionswerte $F(a)$ und $F(b)$ bestimmt.
Wenden wir den Hauptsatz auf das bestimmte Integral $\int\limits_a^b 2x^2 \ dx $ an, dann erhalten wir:
$\displaystyle\int\limits_{-1}^0 2x^2 \ dx = \bigg[ \frac{2}{3} \cdot x^3 \bigg]_{-1}^0 = \bigg( \frac{2}{3} \cdot 0^3 \bigg) - \bigg(\frac{2}{3} \cdot (-1)^3 \bigg) = 0 - \bigg( - \frac{2}{3} \bigg) = \frac{2}{3} \ [FE]$
-
Berechne die Flächenbilanzen der verschiedenen Funktionen.
TippsZum Berechnen der bestimmten Integrale benutzen wir den Hauptsatz der Differential- und Integralrechnung:
$\displaystyle \int\limits_a^b f(x) dx = [F(x)]_a^b = F(b) - F(a)$Wenn du dir nicht sicher bist, ob deine Stammfunktion $F$ auch wirklich eine Stammfunktion ist, dann kannst du dich selbst kontrollieren und die Ableitung von $F$ bilden. Stimmt die Ableitung $F'$ mit der Ausgangsfunktion $f$ überein, dann ist $F$ eine Stammfunktion.
Für eine Potenz $f(x) = x^n$ lässt sich eine Stammfunktion finden, indem wir den Exponenten um eins erhöhen und den Kehrwert als Faktor davor schreiben. Diese Regel heißt Potenzregel. Eine Stammfunktion nach dieser Regel wäre:
$\displaystyle F(x) = \frac{1}{n+1} \cdot x^{n+1}$
LösungRechnerisch bestimmen wir bestimmte Integrale zwischen den Grenzen $a$ und $b$, indem wir den Hauptsatz der Differential- und Integralrechnung anwenden. Dieser lautet:
$ \displaystyle \int\limits_a^b f(x) \ dx = \big[F(x) \big]_a^b = F(b) - F(a)$Mit dem Hauptsatz berechnen wir die bestimmten Integrale und damit die Flächenbilanzen der Funktionen innerhalb der Grenzen:
Erstes Integral:
$\displaystyle \int\limits_{-1}^1 5x^4 - 12x^2 + 9 \ dx = \bigg[ x^5 - 4x^3 + 9x \bigg]_{-1}^1 \\ = \bigg(1^5 - 4 \cdot 1^3 + 9 \cdot 1\bigg) - \bigg( (-1)^5 - 4\cdot (-1)^3 + 9 \cdot (-1) \bigg) = 6 - (-6) = 12 $Zweites Integral:
$\displaystyle \int\limits_0^1 4x^3 - 9x^2 + 2x \ dx = \bigg[ x^4-3x^3+x^2 \bigg]_0^1 \\ = \bigg(1^4 - 3\cdot 1^3 + 1^2\bigg) - \bigg( 0^4 - 3\cdot 0^3 + 0^2 \bigg) = -1 - 0 = -1 $Drittes Integral:
$\displaystyle \int\limits_0^2 \frac{1}{2}x^3 - 3x^2 + 2x + 4 \ dx = \bigg[ \frac{1}{8}x^4 - x^3 + x^2 +4x \bigg]_0^2 \\ = \bigg( \frac{1}{8}\cdot 2^4 - 2^3 + 2^2 +4\cdot 2\bigg) - \bigg(\frac{1}{8}\cdot 0^4 - 0^3 + 0^2 +4\cdot 0 \bigg) = (2 - 8 + 4 +8) - 0 =6 - 0 = 6 $Viertes Integral:
$\displaystyle \int\limits_0^1 \frac{10}{3} x^4 - \frac{1}{2}x^2 \ dx = \bigg[\frac{2}{3} x^5 - \frac{1}{6} x^3 \bigg]_0^1 \\ = \bigg( \frac{2}{3} \cdot 1^5 - \frac{1}{6} \cdot 1^3 \bigg) - \bigg( \frac{2}{3} \cdot 0^5 - \frac{1}{6} \cdot 0^3 \bigg) = \bigg(\frac{2}{3} - \frac{1}{6}\bigg) - 0 = \frac{1}{2} $
9.714
sofaheld-Level
6.600
vorgefertigte
Vokabeln
7.840
Lernvideos
37.241
Übungen
32.630
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Schulstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung







 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?