Sinus, Cosinus, Umkehrfunktionen und Hyperbelfunktionen ableiten

Inhaltsverzeichnis zum Thema

• Wiederholung der trigonometrischen Funktionen und der Hyperbelfunktionen
  • Trigonometrische Funktionen am Einheitskreis
  • Hyperbolische Funktionen
• Ableitungen der trigonometrischen Funktionen
• Ableitungen der hyperbolischen Funktionen
• Zusammenfassung

Wiederholung der trigonometrischen Funktionen und der Hyperbelfunktionen

Trigonometrische Funktionen am Einheitskreis

Als Erstes erinnern wir uns einmal zurück, wie wir die trigonometrischen Funktionen überhaupt definiert haben. Dazu brauchen wir den Einheitskreis (also den Kreis um den Koordinatenursprung mit Radius $1$):

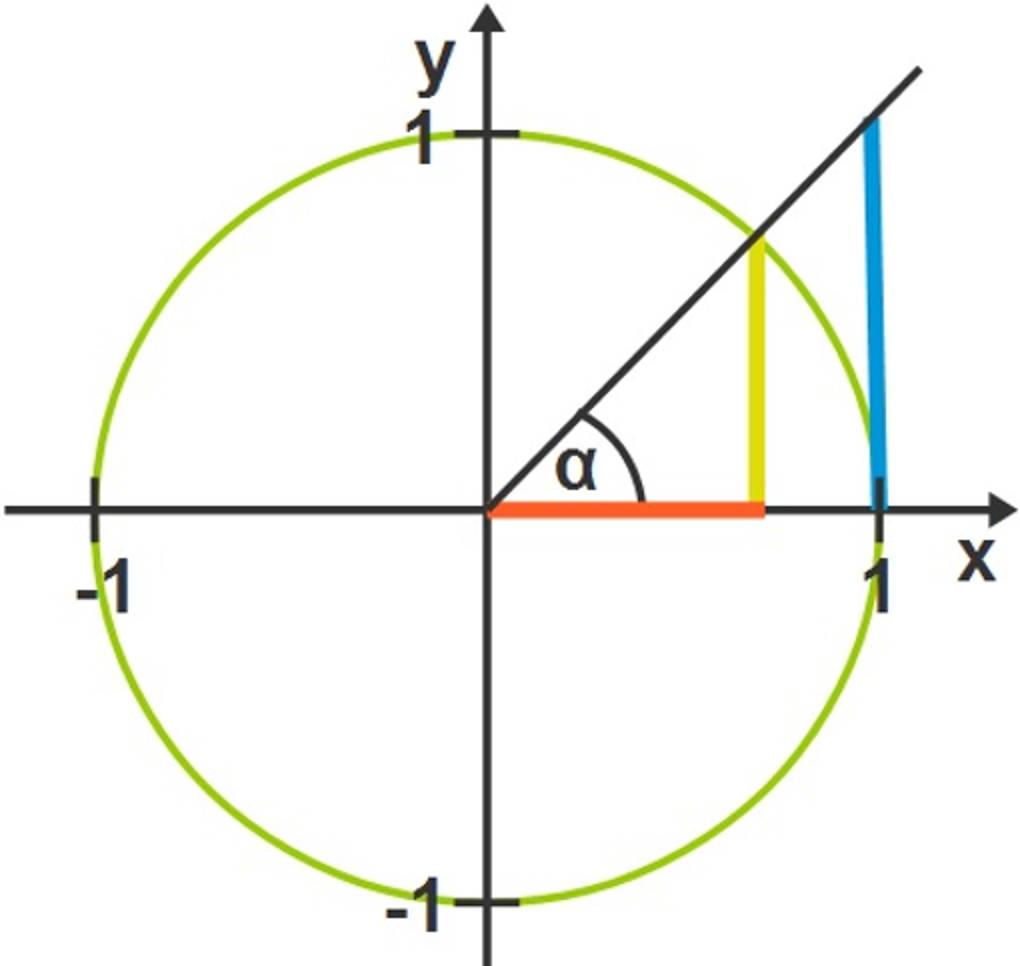
Wir betrachten nun ein rechtwinkliges Dreieck, dessen genaue Form durch den Winkel $\alpha$ bestimmt wird. Hier ist das kleinere der beiden Dreiecke gemeint, die blaue Linie ignorieren wir erst einmal.

Da die Hypotenuse dann der Radius des Einheitskreises ist, hat sie immer die Länge $1$. Außerdem gibt es in dem Dreieck die Ankathete (hier rot), die mit der Hypotenuse den Winkel $\alpha$ einschließt, und die Gegenkathete (hier gelb), die dem Winkel $\alpha$ gegenüberliegt.

Jetzt definieren wir den Sinus und Kosinus des Winkels $\alpha$ folgendermaßen:

$\begin{array}{lllllll} \sin\left(\alpha\right)&=&\dfrac{\text{Ankathete}}{\text{Hypotenuse}}&=&\dfrac{\text{Ankathete}}{1}&=&\text{Ankathete}\\ \cos\left(\alpha\right)&=&\dfrac{\text{Gegenkathete}}{\text{Hypotenuse}}&=&\dfrac{\text{Gegenkathete}}{1}&=&\text{Gegenkathete} \end{array}$

Es ist beim Rechnen mit trigonometrischen Funktionen übrigens grundsätzlich empfehlenswert, den Winkel bzw. die Zahl $\alpha$ im Bogenmaß, also in Vielfachen von $\pi$, anzugeben.

Nun betrachten wir die blaue Linie, also gewissermaßen die Steigung der Hypotenuse des Dreiecks. Wenn wir den Strahlensatz anwenden, finden wir Folgendes heraus:

$ \dfrac{\text{Gegenkathete}}{\text{Ankathete}}=\dfrac{\text{Blaue Linie}}{1} = \text{Blaue Linie}$

Diese blaue Linie nennen wir den Tangens des Winkels $\alpha$. Es gilt also allgemein:

$\tan\left(\alpha\right)=\dfrac{\text{Gegenkathete}}{\text{Ankathete}}=\dfrac{\sin\left(\alpha\right)}{\cos\left(\alpha\right)}$

Hyperbolische Funktionen

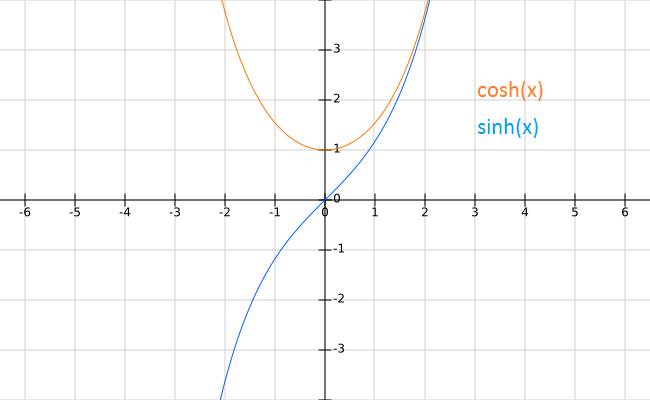
Die hyperbolischen Funktionen – also der Kosinus Hyperbolicus ($\cosh$) und der Sinus Hyperbolicus ($\sinh$) – sind geometrisch etwas umständlicher zu erklären. Deswegen beschränken wir uns hier auf ihre Darstellung als Formeln, die wir auch zum Ableiten brauchen werden. Die Funktionen sind folgendermaßen definiert:

$\begin{array}{lll} \sinh(x) &=& \dfrac{1}{2}\left(e^x-e^{-x}\right) \\ \cosh(x) &=& \dfrac{1}{2}\left(e^x+e^{-x}\right) \end{array}$

Beachte, dass sie sich nur durch das Plus- bzw. Minuszeichen zwischen den Termen in der Klammer unterscheiden.

Ableitungen der trigonometrischen Funktionen

Die Ableitungen der Sinus- und Kosinusfunktionen kannst du dir sehr schön veranschaulichen. Dazu gehst du folgendermaßen vor:

• Zeichne dir eine der Funktionen in ein Koordinatensystem ein.
• Betrachte die Tangenten an einigen ausgewählten Punkten und ergänze die jeweiligen Steigungswerte als Punkte in deinem Koordinatensystem. (Wenn du an der Stelle $x$ die Tangentensteigung $y$ misst, ergänzt du im Koordinatensystem den Punkt $(x\vert y)$.)
• Verbinde die Punkte zu einer neuen Funktion.

Der letzte Schritt klappt natürlich umso besser, je mehr Punkte du vorher eingezeichnet hast. Es ergeben sich die folgenden Ableitungen:

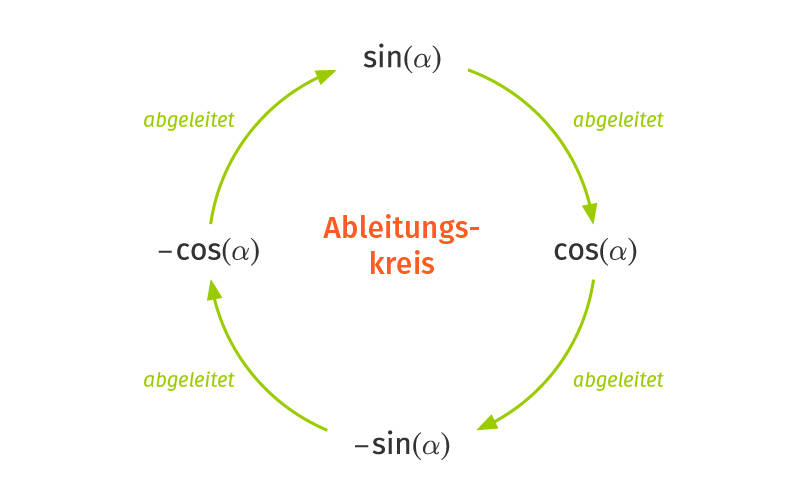
$\begin{array}{lll} (\sin(x))' &=& \cos(x) \\ (\cos(x))' &=& -\sin(x) \end{array}$

Da du die Sinusfunktion mit negativem Vorzeichen mit der Faktorregel wieder ableiten kannst, erhältst du dann eine Kosinusfunktion mit negativem Vorzeichen. Leitest du diese noch einmal ab, ergibt sich wieder eine Sinusfunktion – allerdings wieder mit positivem Vorzeichen. Wenn wir die trigonometrischen Funktionen viermal ableiten, drehen wir uns also gewissermaßen im Kreis und kommen wieder dort an, wo wir angefangen haben.

Wenn wir den Tangens ableiten wollen, erinnern wir uns daran, wie wir ihn definiert haben:

$\tan(x)=\dfrac{\sin(x)}{\cos(x)}$

(Beachte: Das $x$ bezeichnet hier den Winkel, den wir oben $\alpha$ genannt haben.) Wir benötigen also die Quotientenregel. Damit sieht unsere Ableitung folgendermaßen aus:

$\begin{array}{lll} (\tan(x))' &=& \left(\frac{\sin(x)}{\cos(x)}\right)' \\ &=& \dfrac{(\sin(x))'\cdot\cos(x)-\sin(x)\cdot(\cos(x))'}{(\cos(x))^2} \\ &=& \dfrac{\cos(x)\cdot \cos(x)-\sin(x)\cdot(-\sin(x))}{\cos^2(x)} \\ &=& \dfrac{\cos^2(x)+\sin^2(x)}{\cos^2(x)} \\ &=& \dfrac{1}{\cos^2(x)} \end{array}$

Hier haben wir den trigonometrischen Pythagoras ausgenutzt. Dieser beruht auf dem Satz des Pythagoras und lautet:

$\sin^2(x)+\cos^2(x)=1$

Diese Beziehung gilt für jedes $x$! Die Ableitung der Tangensfunktion ist also:

$(\tan(x))'=\dfrac{1}{\cos^2(x)}$

Ableitungen der hyperbolischen Funktionen

Diese Funktionen können wir mit den uns bekannten Regeln ableiten:

• Dank der Faktorregel können wir den Bruch $\frac{1}{2}$ einfach stehen lassen und müssen nur die Klammer ableiten.
• Die Summenregel erlaubt es uns, beide Terme in der Klammer einzeln zu betrachten.
• Die Ableitung der Funktion $e^{a\cdot x}$ ist die Funktion $a\cdot e^{a\cdot x}$.

Sehen wir uns also zuerst die $\sinh$-Funktion an:

$\begin{array}{lll} (\sinh(x))' &=& \left(\frac{1}{2}\left(e^x-e^{-x}\right)\right)' \\ &=& \frac{1}{2}\cdot \left(e^x-e^{-x}\right)' \\ &=& \frac{1}{2}\cdot \left(\left(e^x\right)'-\left(e^{-x}\right)'\right) \\ &=& \frac{1}{2}\cdot\left(e^x-(-1)e^{-x}\right) \\ &=& \frac{1}{2}\cdot\left(e^x+e^{-x}\right) \\ &=& \cosh(x) \end{array}$

Wenn wir die $\cosh$-Funktion auf die gleiche Weise ableiten, erhalten wir folgendes Ergebnis:

$(\cosh(x))' = \sinh(x)$

Es gilt also: Die $\cosh$-Funktion ist die Ableitung der $\sinh$-Funktion und umgekehrt.

Zusammenfassung

Fassen wir noch einmal alle betrachteten Funktionen und ihre Ableitungen zusammen:

$\begin{array}{|c|c|} \hline \text{Funktion} & \text{Ableitung} \\ \hline \sin(x) & \cos(x) \\ \cos(x) & -\sin(x) \\ \tan(x) & \frac{1}{\cos^2(x)} \\ \sinh(x) & \cosh(x) \\ \cosh(x) & \sinh(x) \\ \hline \end{array}$