Lineare Ungleichungssysteme
Halbebenen, Geraden zeichnen
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Lineare Ungleichungssysteme
- Lineare Ungleichungen grafisch darstellen
- Lineare Gleichungen grafisch lösen
- Was ist bei einer linearen Ungleichung zu beachten?
Lineare Ungleichungssysteme
Du lernst in der Schule lineare Gleichungssysteme kennen. Ein lineares Gleichungssystem besteht aus mindestens zwei linearen Gleichungen und oft ebenso vielen Unbekannten.
So sieht das auch bei linearen Ungleichungssystemen aus: Anstelle von linearen Gleichungen liegen hier lineare Ungleichungen vor.
Was ist eine lineare Ungleichung?
Auch hier schauen wir uns zunächst einmal an, was eine lineare Gleichung ist: In einer linearen Gleichung kommen eine oder mehrere Variablen linear vor.
Hier siehst du ein Beispiel für eine lineare Gleichung mit zwei Variablen: $6x-3y=-3$. Diese Gleichung kannst du zum Beispiel nach $y$ umformen. Du subtrahierst $6x$ zu $-3y=-6x-3$ und dividierst schließlich durch $-3$. So erhältst du $y=2x+1$. Diese ist eine lineare Funktionsgleichung, deren Graph eine Gerade ist.
Lineare Ungleichungen grafisch darstellen
Wir beginnen mit einer Wiederholung zu linearen Gleichungen.
Lineare Gleichungen grafisch lösen
Die Gerade zu der Gleichung $y=2x+1$ kannst du zeichnen, indem du
- den $y$-Achsenabschnitt $1$ auf der $y$-Achse einzeichnest. Hier schneidet die Gerade die $y$-Achse.
- Dann zeichnest du ein Steigungsdreieck. In diesem Beispiel gehst du von dem $y$-Achsenabschnitt aus $1$ Einheit nach rechts und $2$ Einheiten nach oben. So erhältst du einen weiteren Punkt auf der Geraden.
- Zeichne die Gerade durch den Schnittpunkt auf der $y$-Achse sowie den im 2. Schritt gefundenen Punkt.
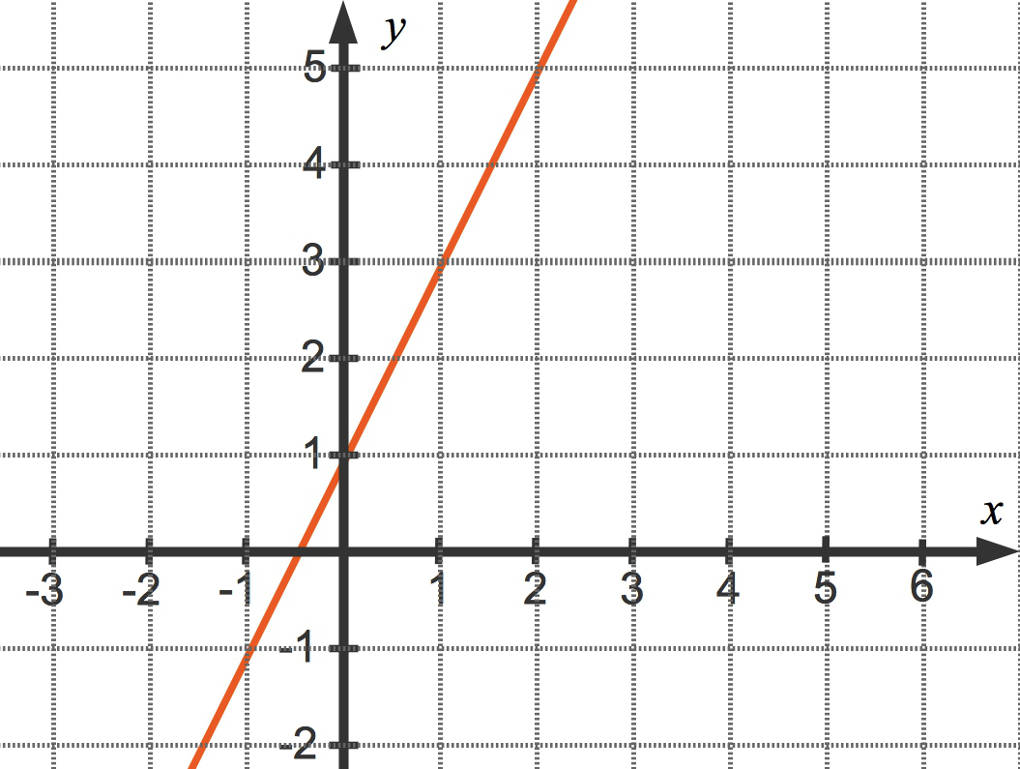
Alle Punkte auf dieser Geraden lösen die lineare Gleichung $6x-3y= -3$.
Was ist bei einer linearen Ungleichung zu beachten?
Wir untersuchen nun die lineare Ungleichung $6x-3y\ge -3$. Du gehst dabei wie folgt vor:
- Zeichne die Gerade, welche du erhältst, wenn du in der Ungleichung $\le$ durch $=$ ersetzt. Diese Gerade wird Randgerade genannt.
- Die Randgerade teilt die Koordinatenebene in zwei Halbebenen. In einer der beiden Halbebenen liegen alle Lösungspaare $(x|y)$ der obigen Ungleichung.
- Du kannst zum Beispiel einen beliebigen Punkt aus einer der beiden Halbebenen auswählen. Erfüllen die Koordinaten dieses Punktes die Ungleichung, so liegt der Punkt in der Lösungshalbebene, andernfalls nicht.
Übrigens: Bei Ungleichungen mit kleiner gleich ($\le$) oder größer gleich ($\ge$) gehört die Randgerade ebenfalls zur Lösungsmenge, ansonsten nicht. Wenn die Randgerade nicht zur Lösungsmenge gehört, kannst du die Gerade gestrichelt zeichnen.
Dies schauen wir uns bei dem obigen Beispiel an: Wir prüfen, ob der Koordinatenursprung $O(0|0)$ die Ungleichung erfüllt, also $6\cdot 0-3\cdot 0\ge -3$ oder $0\ge -3$. Dies ist richtig. Also liegt der Koordinatenursprung in der Lösungsmenge. Diese siehst du im folgenden Bild farbig eingezeichnet.
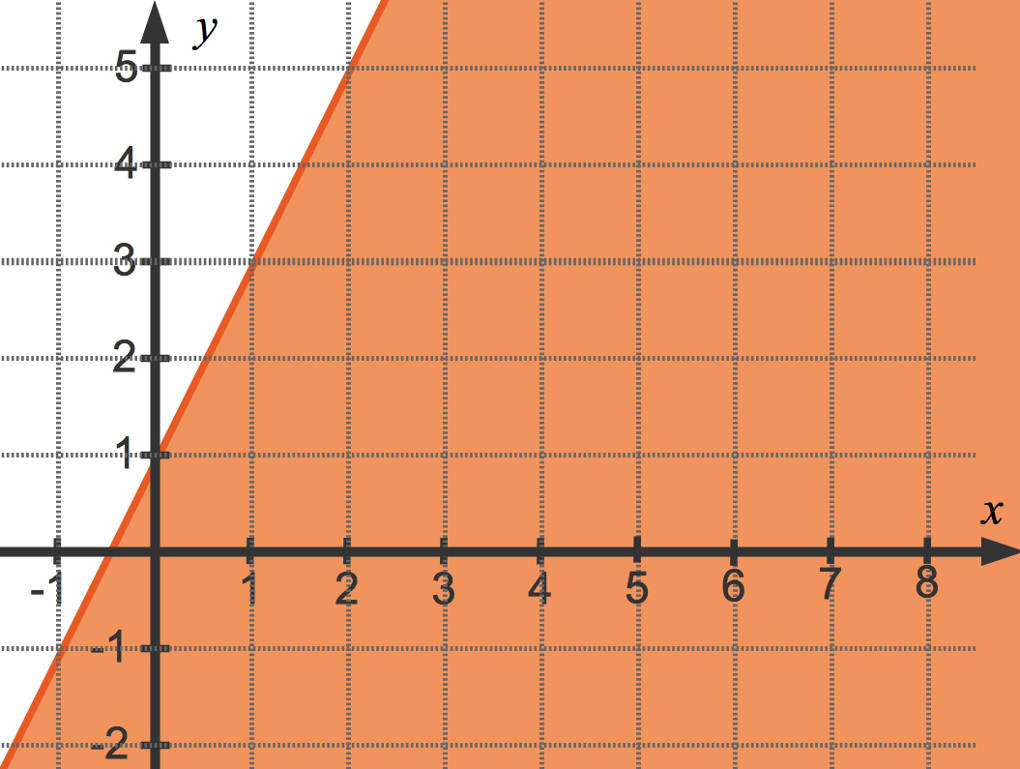
Lineare Ungleichungssysteme grafisch lösen
Wie löst man lineare Ungleichungssysteme graphisch? Wenn du nun mehrere Ungleichungen hast, gehst du für jede einzelne Ungleichung ebenso vor. Schließlich ist die Lösungsmenge des linearen Ungleichungssystems die Schnittmenge aller Lösungsmengen der einzelnen Ungleichungen.
Untersuche das lineare Ungleichungssystem:
(I) $x\ge 0$
(II) $y\ge 0$
(III) $6x-3y\le-3$
(IV) $x+2y\le 8$
Die Lösungsmenge zu (III) ist bereits bestimmt. Wenn du nun die Einschränkungen (I) sowie (II) hinzunimmst, betrachtest du nur den Teil der Lösungsmenge von (III), welcher im I. Quadranten des Koordinatensystems liegt:
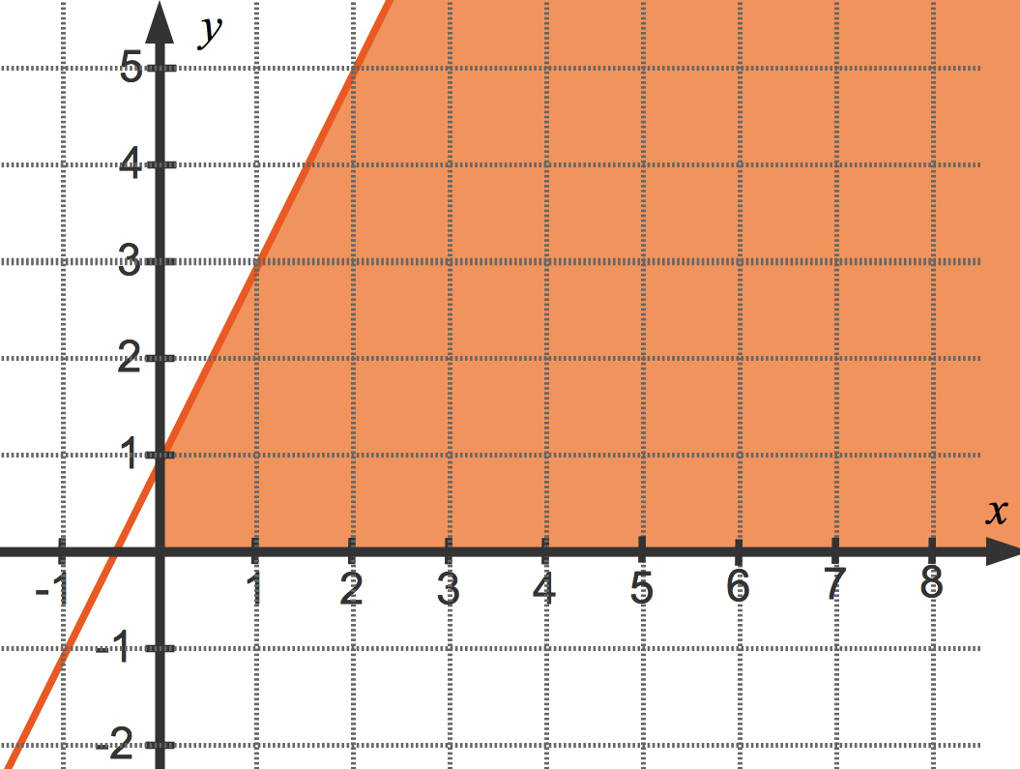
Schließlich formst du die Ungleichung (IV) um zu $y=-\frac12x+4$ und zeichnest hierzu die Randgerade. Du erhältst dann den im Folgenden schraffierten Bereich.
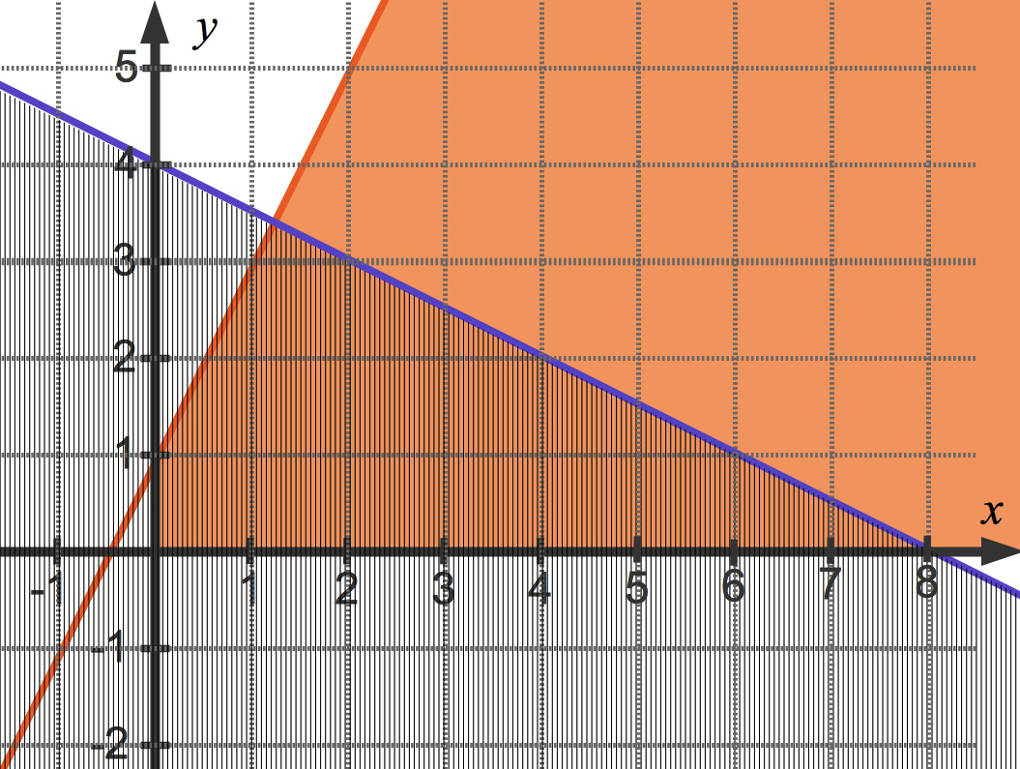
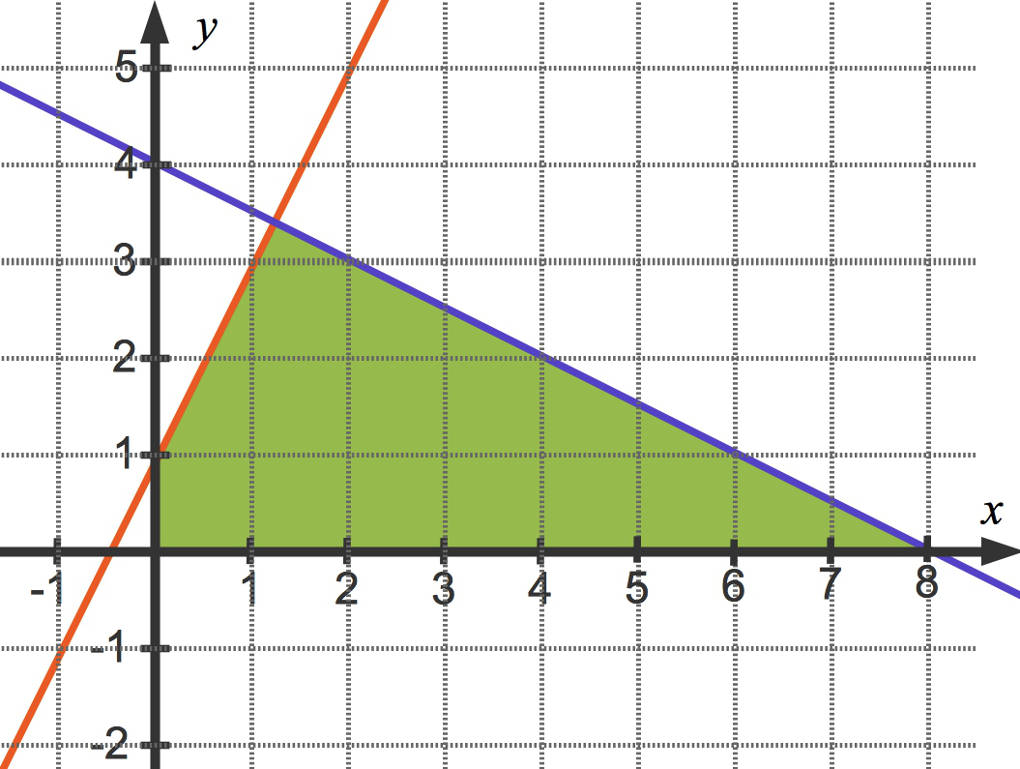
Schließlich sieht die Lösungsmenge des obigen linearen Ungleichungssystems so aus:
Lineare Optimierung
Eine häufige Anwendung von linearen Ungleichungssystemen ist die lineare Optimierung. Es soll der maximale (oder minimale) Wert einer Zielfunktion, zum Beispiel $x+y$, ermittelt werden, unter der Voraussetzung, dass das oben angegebene lineare Ungleichungssystem erfüllt ist.
Du verwendest nun die bereits gefundene Lösungsmenge. Zur Bestimmung der optimalen Lösung $(x|y)$ kannst du entweder die einzelnen Eckpunkte der Lösungsmenge betrachten oder die Gerade zu $x+y=c$, wobei $c$ eine Konstante ist, parallel verschieben. Du verschiebst dabei bis zum äußersten Eckpunkt.
Die grafische Lösung durch Parallelverschiebung der Geraden siehst du in diesem Bild:
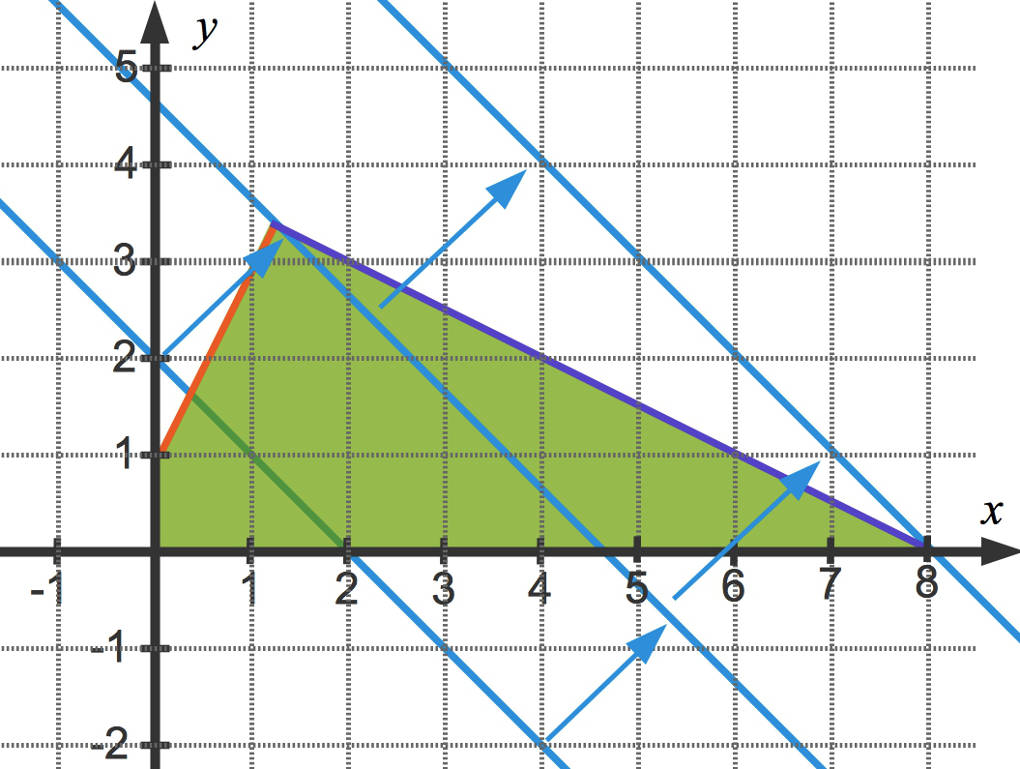
Die optimale Lösung ist also gegeben durch den Punkt $(8|0)$, also $x=8$ sowie $y=0$.
Alle Videos zum Thema
Videos zum Thema
Lineare Ungleichungssysteme (8 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Lineare Ungleichungssysteme (8 Arbeitsblätter)
-
 Lineare Ungleichungssysteme
PDF anzeigen
Lineare Ungleichungssysteme
PDF anzeigen -
 Lineare Ungleichungen mit zwei Variablen – Einführung
PDF anzeigen
Lineare Ungleichungen mit zwei Variablen – Einführung
PDF anzeigen -
 Grafisches Lösen von linearen Ungleichungssystemen
PDF anzeigen
Grafisches Lösen von linearen Ungleichungssystemen
PDF anzeigen -
 Lineare Ungleichungssysteme – Textaufgaben
PDF anzeigen
Lineare Ungleichungssysteme – Textaufgaben
PDF anzeigen -
 Lineares Optimieren – Einführung
PDF anzeigen
Lineares Optimieren – Einführung
PDF anzeigen -
 Grafisches Lösen von linearen Ungleichungssystemen – Übungen
PDF anzeigen
Grafisches Lösen von linearen Ungleichungssystemen – Übungen
PDF anzeigen -
 Grafisches Lösen von linearen Ungleichungen mit 2 Unbekannten
PDF anzeigen
Grafisches Lösen von linearen Ungleichungen mit 2 Unbekannten
PDF anzeigen -
 Systeme linearer Ungleichungen grafisch lösen
PDF anzeigen
Systeme linearer Ungleichungen grafisch lösen
PDF anzeigen
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung



















