Wurzelfunktionen
Was ist eine Wurzelfunktion? Es ist eine Funktion, bei der die Variable unter einer Wurzel steht. Lerne, wie sie als Potenzfunktion dargestellt wird und entdecke die Unterschiede zwischen geraden und ungeraden Exponenten. Interessiert? Mehr dazu im Text!
in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Lerntext zum Thema Wurzelfunktionen
Was ist eine Wurzelfunktion?
Wurzelfunktionen sind Funktionen, bei denen die unabhängige Variable unter einer Wurzel steht.
Allgemeine Form der Wurzelfunktion:
$f (x) = \sqrt[n]{x}$
$n$ ist der Wurzelexponent.
Oft werden Wurzelfunktionen im Mathematikunterricht als Umkehrfunktionen von Potenzfunktionen behandelt.
Potenzfunktion: $f (x) = x^{n}$
Wurzelfunktion: $f (x) = \sqrt[n]{x}$
Wurzelfunktionen als Potenz angeben
Jede Wurzelfunktion lässt sich aufgrund der Potenzgesetze auch als Potenz mit einem Bruch im Exponenten darstellen.
$f (x) = \sqrt[n]{x} = x^{\frac{1}{n}}$
Beispiele für Wurzelfunktionen
Beispiele für Wurzelfunktionen sind:
- $f (x) = \sqrt{x}$
- $f (x) = \sqrt[3]{x}$
- $f (x) = \sqrt[4]{x}$
- $f (x) = \sqrt[5]{x}$
Die Funktion $f (x) = \sqrt{x}= \sqrt[2]{x}$ wird als Quadratwurzelfunktion bezeichnet.
Neben der Quadratwurzel und den angeführten Beispielen lässt sich auch jede andere beliebige Wurzel ziehen und als Wurzelfunktion darstellen. Dabei wird von der n-ten Wurzel gesprochen.
Wurzelfunktionen mit geraden Wurzelexponenten
Wir unterscheiden bei Wurzelfunktionen zwischen Wurzeln mit geraden Exponenten und Funktionen, die Wurzeln mit ungeraden Exponenten aufweisen.
Für Wurzelfunktionen mit geraden Exponenten gilt, dass der Definitionsbereich alle nicht negativen Zahlen umfasst ($\mathbb{D} = \mathbb{R}^{+}_{0}$), denn aus negativen Zahlen lassen sich keine Wurzeln mit geraden Exponenten, wie beispielsweise die Quadratwurzel, ziehen.
Welche Eigenschaften haben Wurzelfunktionen mit geraden Wurzelexponenten?
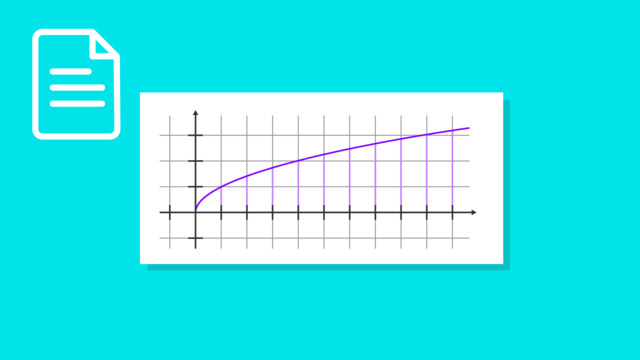
Wurzelfunktionen mit geraden Wurzelexponenten sind streng monoton steigend. Je höher der Wurzelexponent ist, desto „flacher“ verläuft die Funktion.
Alle Wurzelfunktionen mit geraden Wurzelexponenten, die nicht gestreckt, gestaucht oder verschoben sind, verlaufen durch die Punkte $(0|0)$ und $(1|1)$.
Das Minimum $(0|0)$ einer solchen Wurzelfunktion ist zugleich ihre einzige Nullstelle.
Wurzelfunktionen mit ungeraden Wurzelexponenten
Bei Wurzelfunktionen mit ungeraden Exponenten ist die Sachlage etwas anders.
Für sie gilt, dass ihr Definitionsbereich alle reellen Zahlen umfasst ($\mathbb{D} = \mathbb{R}$). Anders als bei Wurzelfunktionen mit geraden Wurzelexponenten sind hier auch negative reelle Zahlen möglich, denn aus negativen Zahlen können Wurzeln mit ungeraden Wurzelexponenten gezogen werden.
$\sqrt[3]{- 1} = -1$, da $(- 1) \cdot (- 1) \cdot (- 1)=-1$
Auch die Wertemenge der Funktion besteht aus den reellen Zahlen:
$\mathbb{W} = \mathbb{R}$.
Welche Eigenschaften haben Wurzelfunktionen mit ungeraden Wurzelexponenten?
Auch für Wurzelfunktionen mit ungeraden Wurzelexponenten gilt: Je höher der Wurzelexponent ist, desto „flacher“ verläuft die Funktion.
Alle Wurzelfunktionen mit ungeraden Wurzelexponenten, die nicht gestreckt, gestaucht oder verschoben sind, verlaufen durch die Punkte $(-1|-1)$, $(0|0)$ und $(1|1)$.
Wurzelfunktionen – Zusammenfassung
Bei Wurzelfunktionen steht die unabhängige Variable unter einer Wurzel. Die allgemeine Form der Wurzelfunktion ist:
$f (x) = \sqrt[n]{x}$
Unterschieden wird zwischen Wurzelfunktionen mit geraden Wurzelexponenten und Wurzelfunktionen mit ungeraden Wurzelexponenten.
Für Wurzelfunktionen mit geraden Wurzelexponenten gilt:
- $\mathbb{D} = \mathbb{R}^{+}_{0}$
- $\mathbb{W} = \mathbb{R}^{+}_{0}$
Für Wurzelfunktionen mit ungeraden Wurzelexponenten gilt:
- $\mathbb{D} = \mathbb{R}$
- $\mathbb{W} = \mathbb{R}$
9.863
sofaheld-Level
6.600
vorgefertigte
Vokabeln
7.800
Lernvideos
37.183
Übungen
32.618
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Schulstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung


 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?