Rekonstruktion ganzrationaler Funktionen – Lösungsstrategie


in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Grundlagen zum Thema Rekonstruktion ganzrationaler Funktionen – Lösungsstrategie
Dieses Video zeigt, wie du vorgehen kannst, um ganzrationale Funktionen zu rekonstruieren. Nachdem wir die wichtigsten Eigenschaften ganzrationaler Funktionen wiederholt haben, schauen wir uns an einer konkreten Beispielaufgabe gemeinsam an, wie man vorgehen kann, um eine Funktion zu rekonstruieren. Was das mit einer bestimmten Anzahl an Bedingungen zu tun hat, erfährst du im Video ebenfalls. Viel Spaß beim Schauen!
Rekonstruktion ganzrationaler Funktionen – Lösungsstrategie Übung
-
Gib die Eigenschaften einer ganzrationalen Funktion wieder.
TippsEine Extremstelle ist ein Hochpunkt oder ein Tiefpunkt. An dieser Stelle liegt eine waagerechte Tangente vor. Die Steigung ist also $0$.
Wenn du einen Funktionswert berechnen möchtest, setzt du einen Wert für $x$ in die Funktionsgleichung ein.
Dies kannst du hier für $x=-2$ sehen.
Achte darauf, negative Zahlen beim Potenzieren zu klammern.
In einem Wendepunkt hat der Graph einen Krümmungswechsel.
Die zweite Ableitung steht für die Krümmung.
LösungWas heißt eigentlich rekonstruieren? Wenn eine ganzrationale Funktion rekonstruiert werden soll, dann muss man sich zunächst einige Eigenschaften einer solchen Funktion klar machen.
Bei einer Kurvendiskussion ist eine Funktionsgleichung vorgegeben und es sollen charakteristische Punkte des Funktionsgraphen bestimmt werden. Schließlich soll der Funktionsgraph gezeichnet werden.
Bei einer Rekonstruktion ist dies genau umgekehrt: Es sind charakteristische Punkte (oft in Form einer Skizze) vorgegeben. Gesucht ist dann die Funktionsgleichung.
Ganz allgemein gilt, dass man zur Rekonstruktion einer ganzrationalen Funktion vom Grad $n$ genau $n+1$ Angaben benötigt. Damit stellt man ein Gleichungssystem auf und löst dieses.
Hierfür sollte man Folgendes wissen:
- Wenn man zu einem $x$ den Funktionswert berechnen möchte, setzt man dieses $x$ in die Funktionsgleichung ein. Zum Beispiel ist für $f(x)=x^2+3x$ der Funktionswert für $x=-1$ gegeben durch $f(-1)=(-1)^2+3\cdot (-1)=1-3=-2$. So erhält man den Punkt $(-1|-2)$ des Funktionsgraphen.
- Eine Nullstelle einer Funktion erhält man durch Lösen der Gleichung $f'(x)=0$.
- Liegt an einer Stelle eine Extremstelle vor, so gibt es dort eine waagerechte Tangente. Das bedeutet, es gilt $f'(x)=0$ – die Steigung ist $0$.
- Liegt an einer Stelle eine Wendestelle vor, so gibt es dort einen Krümmungswechsel. Das bedeutet, es gilt $f''(x)=0$.
-
Stelle das Gleichungssystem zur Rekonstruktion der Funktion auf.
TippsAn einer Extremstelle ist die erste Ableitung gleich $0$.
Da der Hochpunkt bekannt ist, weißt du insbesondere, dass
$f(-1)=-1$ ist.
Setze $-1$ in der Funktionsgleichung ein.
Für den y-Achsenabschnitt gilt $x=0$.
Es ist $f(0)=d$.
Führe eine Probe mit der gefundenen Funktion durch.
LösungZunächst ist die gesuchte Funktion kubisch. Das bedeutet, dass sie den Grad $3$ hat. Dies erkennt man zum einen an dem Beginn der Funktion $f(x)=2x^3...$ sowie an deren Verlauf.
Allgemein lautet eine kubische Funktion
$f(x)=ax^3+bx^2+cx+d$.
Hier ist $a=2$ bereits bekannt. Es werden somit noch drei Angaben benötigt.
- Ein Punkt des Graphen ist bekannt $(-1|-1)$. Somit gilt $f(-1)=-1$.
- Dieser Punkt ist ein Hochpunkt, also ein Extrempunkt. Es liegt also eine waagerechte Tangente vor mit $f'(-1)=0$.
- Der Graph schneidet die y-Achse bei $-3$.
- $f(x)=2x^3+bx^2+cx+d$
- $f'(x)=6x^2+2bx+c$
- $f(-1)=-1$ führt zu $-2+b-c+d=-1$.
- $f'(-1)=0$ führt zu $6-2b+c=0$.
- $y=-3$ führt mit $x=0$ zu $d=-3$.
$\begin{array}{rclll} -2+b-c-3&=&-1&|&+5\\ b-c&=&4 \end{array}$
Dann die 2. Gleichung:
$\begin{array}{rclll} 6-2b+c&=&0&|&-6\\ -2b+c&=&-6 \end{array}$
Zuletzt werden diese beiden Gleichungen addiert und man erhält
$-b=-2$. Multiplikation mit $-1$ führt zu $b=2$.
Setzt man diesen Wert für $b$ in eine der beiden letzten Gleichungen ein, erhält man $2-c=4$. Addition von $c$ und Subtraktion von $4$ führt zu $c=-2$.
Die gesuchte Gleichung lautet also $f(x)=2x^3+2x^2-2x-3$.
-
Leite das Gleichungssystem der kubischen Funktion her.
TippsHier siehst du die Ableitung der Funktion.
Bei einer Extremstelle ist die 1. Ableitung gleich $0$.
Bei einer Nullstelle ist die Funktion gleich $0$.
Die Stelle, an welcher eine ganzrationale Funktion die y-Achse schneidet, ist immer der Term, in welchem kein $x$ vorkommt.
LösungHier ist die allgemeine Form einer kubischen Funktionsgleichung zu sehen sowie deren Ableitung.
Gesucht sind die Koeffizienten $a$, $b$, $c$ und $d$.
Das bedeutet, dass man vier Bedingungen benötigt.
- Es liegt eine Extremstelle bei $x=1$ vor. Man setzt $x=1$ in die erste Ableitung ein und diese muss $0$ sein: $3a+2b+c=0$.
- $x=1$ ist auch eine Nullstelle. Nun wird $x=1$ in die Funktionsgleichung eingesetzt und es muss $0$ herauskommen: $a+b+c+d=0$.
- $x=-1$ ist ebenfalls eine Nullstelle. Analog wird $x=-1$ in die Funktionsgleichung eingesetzt und es muss $0$ herauskommen: $-a+b-c+d=0$. Wichtig ist zu beachten, dass $(-1)^n$ für ungerade $n$ immer $-1$ ergibt.
- Der Graph der Funktion schneidet die y-Achse bei $y=1$. Dies führt zu $f(0)=1$, also $d=1$.
$f(x)=a_nx^n+...+a_1x+a_0$.
$a_0$ ist immer die Stelle, an welcher der Graph der Funktion die y-Achse schneidet.
-
Ermittle die Funktionsgleichung durch Lösen des Gleichungssystems.
TippsForme jede der Gleichungen so um, dass auf der linken Seite nur die unbekannten Koeffizienten stehen und auf der rechten Seite Konstanten.
Wenn in zwei Gleichungen die Unbekannten mit gemeinsamen Faktoren, aber verschiedenen Vorzeichen auftauchen, kannst du diese addieren.
Ein Beispiel siehst du hier.
Führe eine Probe durch.
- $x=1$ ist Extrem- sowie Nullstelle von $f(x)$.
- $x=-1$ ist Nullstelle von $f(x)$.
LösungDa der Wert für $d$ bereits bekannt ist, wird dieser in die Gleichung (II) sowie (III) eingesetzt und man erhält nach Subtraktion von $-1$ in beiden Gleichungen:
- (II)' $a+b+c=-1$
- (III)' $-a+b-c=-1$.
$\begin{array}{rclll} 2b&=&-2&|&:2\\ b&=&-1. \end{array}$.
Dieses $b$ wird in die Gleichung (III)' sowie (I) eingesetzt:
- (I)' $3a-2+c=0$, was äquivalent ist zu $3a+c=2$ sowie
- (III)'' $-a-1-c+1=0$; dies ist wiederum äquivalent zu $-a-c=0$.
$2a=2$.
Division durch $2$ führt zu $a=1$. Wenn man dieses $a$ zum Beispiel in (III)'' einsetzt, gelangt man zu $-1-c=0$. Addition von $c$ führt zu $c=-1$.
Somit sind alle Koeffizienten bekannt und man kann die Funktionsgleichung aufstellen:
$f(x)=x^3-x^2-x+1$.
-
Beschreibe den Weg zur Rekonstruktion einer ganzrationalen Funktion.
TippsEine quadratische Funktion lautet allgemein
$f(x)=ax^2+bx+c$.
Gesucht sind also die drei (!) Koeffizienten $a$, $b$ und $c$.
Beachte:
- Für Nullstellen ist die Funktion $f(x)=0$.
- Für Extremstellen ist die erste Ableitung $f'(x)=0$.
- Für Wendestellen ist die zweite Ableitung $f''(x)=0$.
Schau dir folgendes Beispiel an: $f(x)=ax+b$.
Bekannt sind die Punkte $(3|0)$ sowie $(0|3)$. Damit erhältst du
- $3a+b=0$
- $b=3$.
LösungDer folgende Weg hilft beim Rekonstruieren von ganzrationalen Funktionen weiter:
- Es werden Bedingungen formuliert mit Hilfe der Funktion $f(x)$ sowie den Ableitungen $f'(x)$ und $f''(x)$.
- Für Funktionen vom Grad $n$ werden immer $n+1$ Bedingungen benötigt. Mit Hilfe dieser Bedingungen wird ein Gleichungssystem aufgestellt.
- Dieses Gleichungssystem wird gelöst. Somit ergeben sich die Koeffizienten der gesuchten Funktion und damit die Funktionsgleichung.
- Zur Kontrolle kann man eine Probe durchführen, indem ein Punkt (oder mehrere) in die Funktionsgleichung eingesetzt wird.
-
Stelle die kubische Funktionsgleichung auf.
TippsBeachte: Du benötigst vier Bedingen. Jeder der beiden gegebenen Punkte ist ein Extrempunkt und liefert somit zwei Bedingungen.
Sei $E(a|b)$ ein Extrempunkt, so erhältst du die Bedingungen
- $f(a)=b$ sowie
- $f'(a)=0$.
Du erhältst das Gleichungssystem.
- (I) $a+b+c+d=5$
- (II) $3a+2b+c=0$
- (III) $27a+9b+3c+d=1$
- (IV) $27a+6b+c=0$
Subtrahiere von der Gleichung (III) die Gleichung (I).
Nun hast du drei Gleichungen in zwei Unbekannten.
- (II) $3a+2b+c=0$
- (IV) $27a+6b+c=0$
- (V) $13a+4b+c=-2$
Eliminiere nun $c$.
LösungDie gesuchte Funktion ist kubisch. Das bedeutet
$f(x)=ax^3+bx^2+cx+d$.
Die Ableitung dieser Funktion ist gegeben durch
$f'(x)=3ax^2+2bx+c$.
Es sind zwei Extremstellen bekannt: Der Hohe Euler $E(1|5)$ und das Gauß-Tal $G(3|1)$. Die Art des Extremums liefert keine weitere Bedingung für eine Rekonstruktionsaufgabe.
Der Hohe Euler führt zu den Gleichungen
- $f(1)=5$ $\rightarrow$ (I) $a+b+c+d=5$ und
- $f'(1)=0$ $\rightarrow$ (II) $3a+2b+c=0$.
- $f(3)=1$ $\rightarrow$ (III) $27a+9b+3c+d=1$ sowie
- $f'(3)=0$ $\rightarrow$ (IV) $27a+6b+c=0$.
(V) $13a+4b+c=-2$.
Nun wird $c$ eliminiert:
- (IV) $-$ (II) führt zu $24a+4b=0$ oder, nach Division durch $4$, zu
- (VI) $6a+b=0$.
- (V) $-$ (II) führt zu $10a+2b=-2$. Division durch $2$ liefert
- (VII) $5a+b=-1$.
Nun wird (werden) die jeweils gefundene(n) Variable(n) in den Gleichungen eingesetzt:
- $a=1$ in (VII) führt zu $5+b=-1$. Subtraktion von $5$ resultiert in $b=-6$.
- $a=1$ und $b=-6$ in (II): $3-12+c=0$. Durch Addition von $9$ gelangt man zu $c=9$.
- $a=1$, $b=-6$ und $c=9$ in (I) $1-6+9+d=5$. Es wird $4$ subtrahiert und man erhält $d=1$.
$f(x)=x^3-6x^2+9x+1$.
9.859
sofaheld-Level
6.600
vorgefertigte
Vokabeln
7.800
Lernvideos
37.183
Übungen
32.618
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Schulstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung




 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?
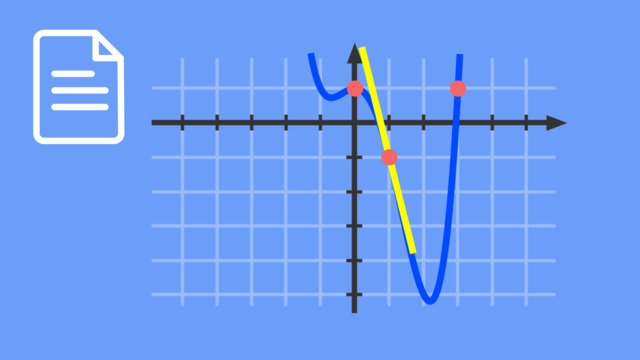











Hallo @Daniela H.,
wir betrachten hier eine Funktion 3. Grades, also allgemein f(x)=ax^3+bx^2+cx+d. Nun können wir erkennen, dass a=2 ist und haben somit den Ansatz f(x)=2x^3+bx^2+cx+d. Wir kennen zudem den Punkt, in dem der Graph die y-Achse schneidet, nämlich S(0|-3). Jetzt können wir diesen Punkt in unsere Funktionsgleichung einsetzen und erhalten f(0)=2*0^3+b*0^2+c*0+d=-3. Alle Produkte mit dem Faktor Null sind Null und fallen hier weg, übrig bleibt das absolute Glied d=-3.
Liebe Grüße aus der Redaktion.
Hey, klasse Video ersteinmal, doch habe ich eine Frage. Wie kommt man in der Lösungsstrategie auf d ist gleich -3 ?
Villeicht kann mir jemand das noch einmal einfach erläutern?
@Yoon Sojina:
Das ist alles richtig gerechnet. Dass f ''(3)=0 ist, bedeutet, dass x=3 kein Extrempunkt ist, also kein Hoch- oder Tiefpunkt. Ein Sattelpunkt kann es trotzdem sein, da ein Sattelpunkt kein Extrempunkt ist, sondern nur zufällig auch die Steigung 0 hat.
Viel Erfolg beim Lernen wünscht Sofatutor!
etwas stimmt nicht. In der folgend Funkion: f(x)=1/3x4-8/3x3+6x2 , wenn x=3 ist, f´(x)=0, und f´´(x)=0. und f´´´(3) ist 8, ungleich null. Und (3,9) ist trotzdem ein Sattelpunkt, weil f´(x)=0 ist. Bitte erklären!
Die Bedingung dass ein Sattelpunkt vorliegt ist nicht, dass f´´´(x) ungleich null ist. Dies ist doch lediglich Teil der hinreichende Bedingung für einen Wendestelle. Um herauszufinden ob es ein Sattelpunkt ist muss zusätzlich f`(x) für diese Stelle gleich null sein!