Netze von Körpern
Was ist überhaupt ein Körpernetz? Du kannst ein Körpernetz wie eine Bastelvorlage für einen Körper verstehen.
Inhaltsverzeichnis zum Thema
Was ist ein Körpernetz?
Ein Körpernetz entsteht, wenn man einen geometrischen Körper auffaltet. Hierfür musst du den Körper an seinen Kanten aufschneiden.
Übrigens: Du kannst nicht zu jedem Körper ein Netz zeichnen. Zu einer Kugel gibt es kein Körpernetz.
Ein Körpernetz ist also eine ebene Darstellung eines Körpers. Eine weitere ebene Darstellung eines Körpers ist dessen Schrägbild.
Körpernetze kannst du auch als Bastelvorlage verwenden oder zur Veranschaulichung bei der Berechnung der Mantelfläche beziehungsweise Oberfläche eines Körpers.
Netze von Prismen
Wir beginnen mit den Körpernetzen von Prismen. Ein Prisma hat als Grundfläche ein Vieleck und parallel dazu eine kongruente Deckfläche. Die Ecken der Grund- und Deckfläche sind durch parallele und gleich lange Seitenkanten miteinander verbunden. Diese stehen senkrecht zu der Grund- und Deckfläche. Die Länge dieser Kanten wird als Höhe des Prismas bezeichnet.
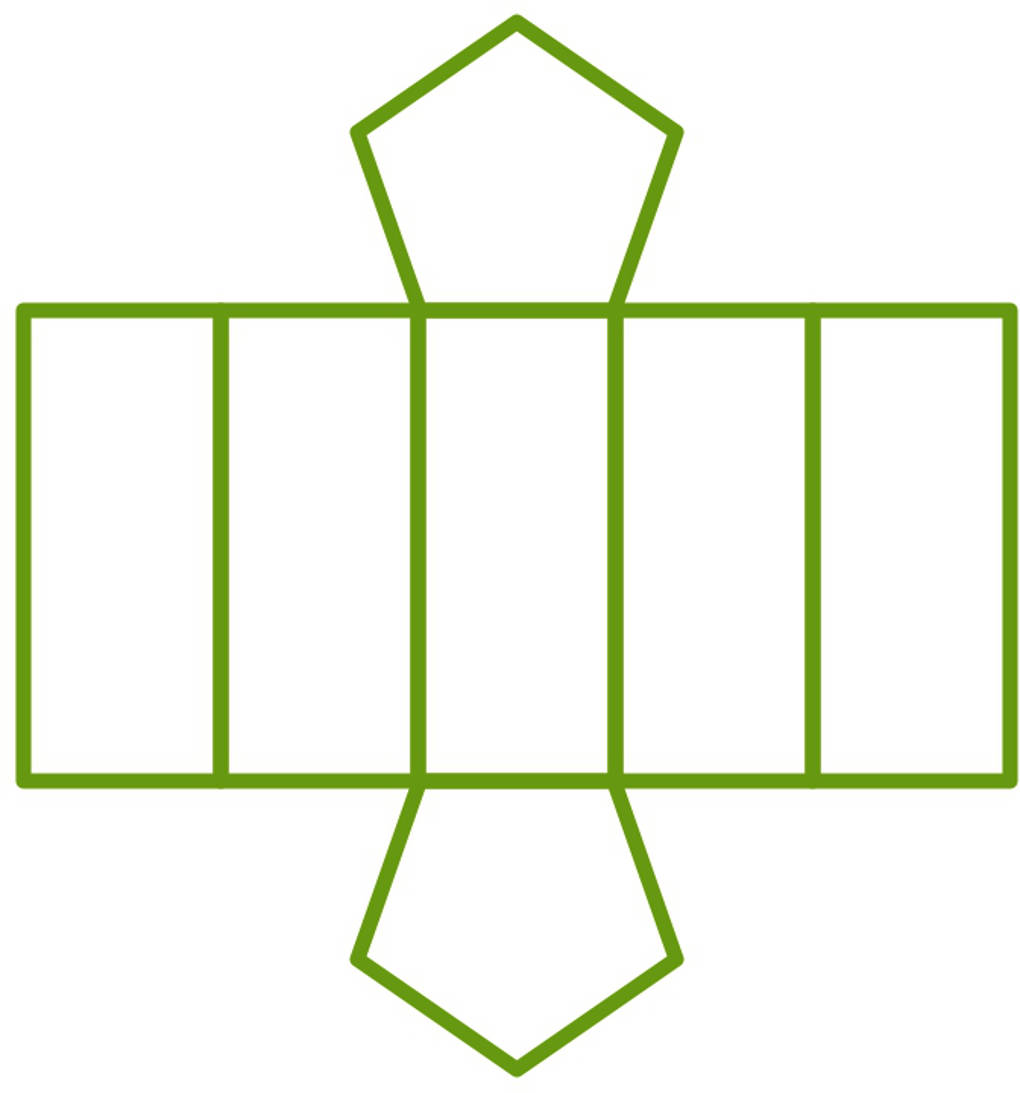
Wir betrachten nun ein Prisma mit einer fünfseitigen Grundfläche. Das resultierende Netz des Prismas besteht aus zwei Fünfecken, der Grund- und der Deckfläche, sowie fünf Rechtecken, den Seitenflächen.
Du kannst dieses Netz eines Prismas so erzeugen: Du stellst die Grundfläche des Prismas auf ein Blatt Papier und zeichnest diese ab. Dann kippst du das Prisma auf eine Seitenfläche. Auch diese zeichnest du ab. Nun rollst du das Prisma über die übrigen Seitenflächen sowie die Deckfläche ab. Auch diese Flächen überträgst du jeweils auf das Blatt Papier. Dieses Vorgehen wird als Abrollmethode bezeichnet. Am Schluss hast du das Netz auf dein Blatt Papier übertragen:
Netze von Zylindern
Das Netz eines Zylinders besteht aus zwei Kreisen, der Deck- und Grundfläche, sowie einem Rechteck als Mantelfläche.
Falls es dich verblüfft, dass die Mantelfläche eines Zylinders ein Rechteck ist, kannst du einmal eine Küchenrolle entlang der Höhe aufschneiden. Klappst du die aufgeschnittene Rolle auf, erhältst du ein Rechteck.
Hier siehst du ein Zylindernetz:
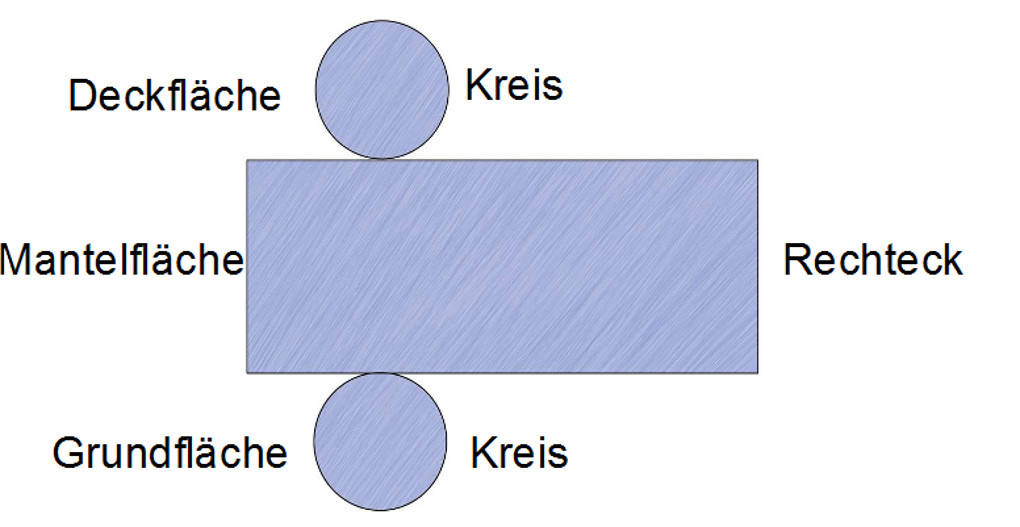
Übrigens: Nicht jede Anordnung von zwei Kreisen und einem Rechteck ist auch automatisch ein Zylindernetz. Was ist zu beachten?
- Die Seitenlängen des Mantels sind die Höhe des Zylinders sowie der Umfang des Grund- beziehungsweise Deckkreises.
- Die Kreise müssen auf zwei gegenüberliegenden Seiten des Mantels anliegen.
Netze von Kegeln
Nun schauen wir uns noch einen Kegel an. Die Grundfläche eines Kegels ist ein Kreis. Jeder Punkt des Kreisrandes wird mit der Spitze des Kegels verbunden.
Hier im Bild siehst du links einen Kegel und rechts das zugehörige Kegelnetz:
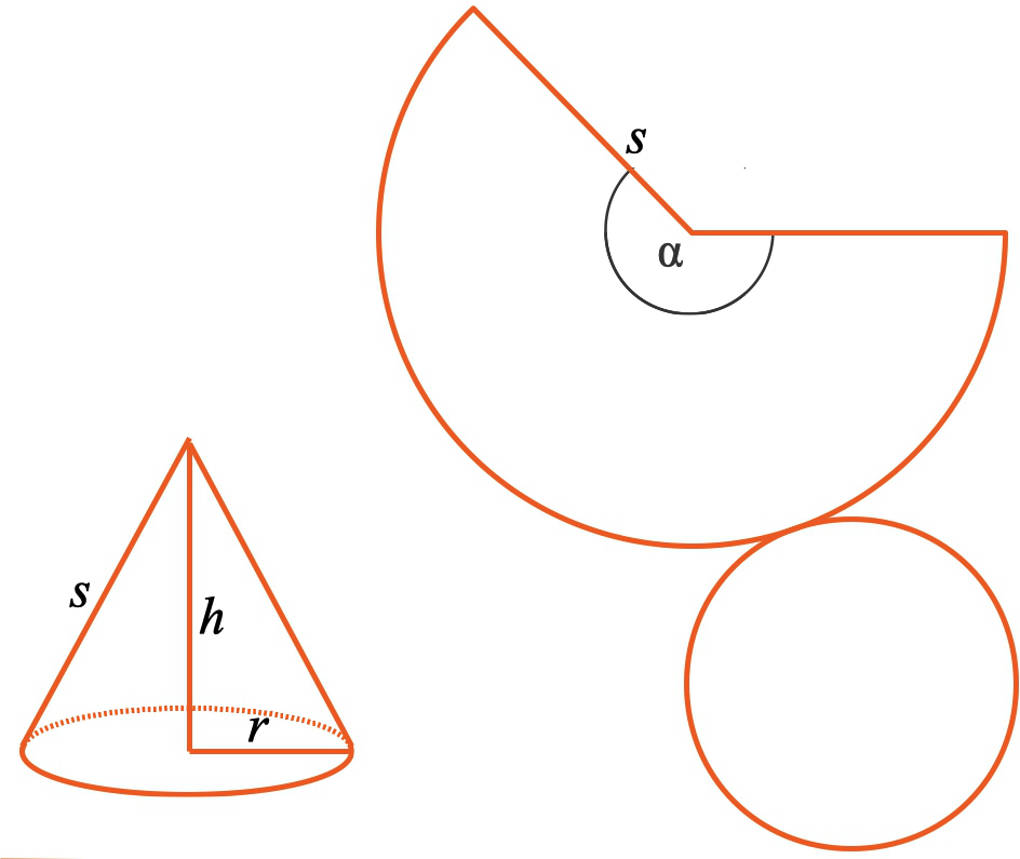
Du kannst erkennen, dass dieses Netz aus der Grundfläche, also dem Kreis, sowie dem Mantel besteht. Der Mantel ist ein Kreissegment. Der Bogen dieses Kreissegmentes ist ebenso lang wie der Umfang des Kreises, welcher als Grundfläche dient.
Wie kannst du dieses Kreissegment konstruieren? Der Radius $s$ des Kreissegments ist gerade die Kante $s$ des Kegels. Wenn zum Beispiel der Radius $r$ der Grundfläche und die Höhe $h$ des Kegels gegeben sind, kannst du $s$ mithilfe des Satzes von Pythagoras ermitteln: $s=\sqrt{r^{2}+h^{2}}$.
Der Mittelpunktwinkel des Kreissegmentes ist gegeben durch $\alpha=\frac{r}{s}\cdot 360^{\circ}$. Nun kannst du das Kreissegment konstruieren.
Übrigens: Auch die Netze von Zylindern oder Kegeln kannst du mithilfe der Abrollmethode erstellen.
Alle Videos zum Thema
Videos zum Thema
Netze von Körpern (3 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Netze von Körpern (3 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung





 Netze von geraden Prismen
Netze von geraden Prismen
 Netze von Zylindern
Netze von Zylindern
 Netze von Kegeln
Netze von Kegeln









