Abgrenzung lineares und exponentielles Wachstum
.
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
Was ist Wachstum?
Wachstum bedeutet in der Mathematik die Zunahme oder auch Vergrößerung einer Größe in Abhängigkeit von der Zeit.
Wir schauen uns einmal ein Beispiel an: Herr Oskar hat eine neue Arbeitsstelle. Zu Beginn erhält er einen Lohn in Höhe von $3500$ €. Er vereinbart mit seinem Arbeitgeber, dass der Lohn nach einem Jahr auf $3800$ € angehoben wird und nach weiteren zwei Jahren auf $4000$ €. Du siehst, der Lohn steigt an. Es liegt also Wachstum vor.
Ein solches Wachstum kannst du zum Beispiel in einem Koordinatensystem darstellen:
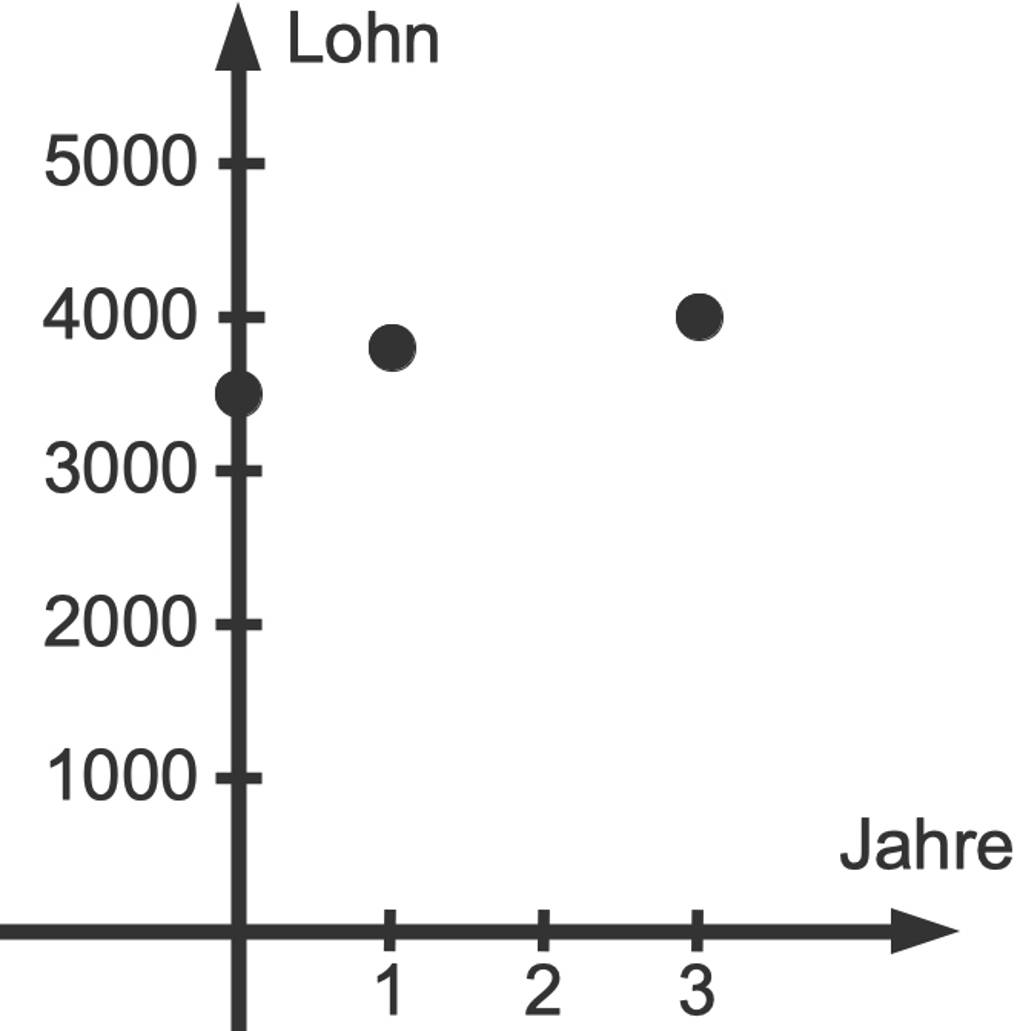
Nun schauen wir uns lineares Wachstum sowie exponentielles Wachstum an. Hierbei widmen wir uns insbesondere der Frage, wie diese beiden voneinander unterschieden werden können.
Eigenschaften von linearem Wachstum
Bei linearem Wachstum liegt eine konstante Änderung vor. Was bedeutet das? In gleichen Abständen kommt immer die gleiche Menge (der gleiche Betrag) dazu.
Übrigens: So kannst du auch lineare Abnahme erklären. In gleichen Abständen wird immer der gleiche Betrag abgezogen.
Präge dir den folgenden Merksatz ein: Nimmt in gleichen Abschnitten ein abhängiger Wert $y$ immer um den gleichen Wert $d$ zu, so heißt diese Zunahme lineares Wachstum.
Wenn du lineares Wachstum in ein Koordinatensystem einzeichnest, erhältst du eine Gerade:
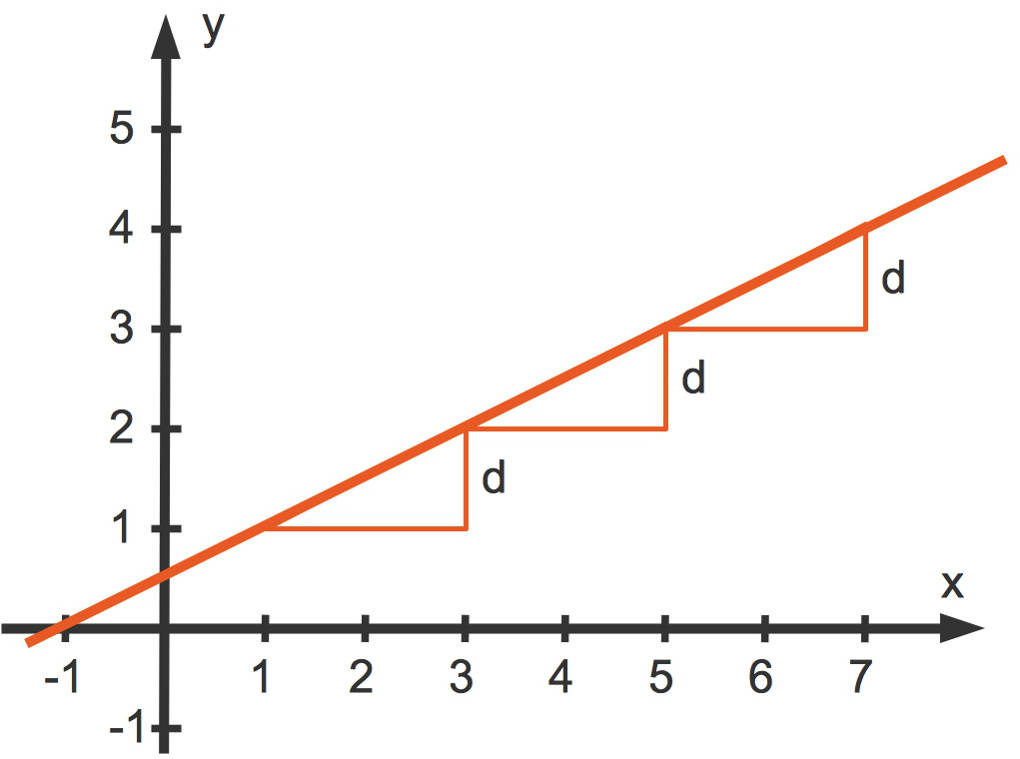
Wir schauen uns dies an dem Beispiel von Herrn Oskar an. Die Entwicklung seines Lohns stellt ihm sein Arbeitgeber in Form einer Tabelle dar:
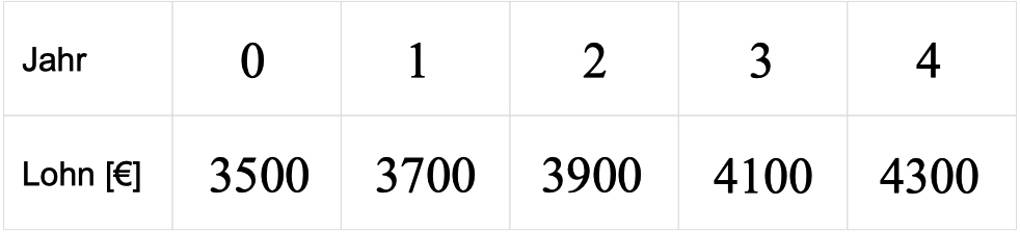
Wenn du jeweils die Differenz zweier aufeinanderfolgender Werte bildest, erhältst du:
- Wert im Jahr $1$ minus Wert im Jahr $0$: $3700~\text{€}-3500~\text{€}=200~\text{€}$
- Wert im Jahr $2$ minus Wert im Jahr $1$: $3900~\text{€}-3700~\text{€}=200~\text{€}$
- Wert im Jahr $3$ minus Wert im Jahr $2$: $4100~\text{€}-3900~\text{€}=200~\text{€}$
Du siehst, die Differenz ist immer gleich.
Du kannst zu linearem Wachstum auch eine Funktionsgleichung aufstellen. Diese ist eine lineare Funktion, in diesem Beispiel $f$ mit $f(x)=200\cdot x+3500$.
Zusammenfassend kannst du lineares Wachstum so untersuchen:
- Aufeinanderfolgende Werte unterscheiden sich immer um den gleichen Betrag.
- Die Darstellung in einem Koordinatensystem ist eine Gerade.
- Die zugehörige Funktionsgleichung ist eine lineare Funktion.
Eigenschaften von exponentiellem Wachstum
Exponentielles Wachstum liegt vor, wenn sich eine Größe in jeweils gleichen Abschnitten immer um denselben Faktor verändert.
Auch hierfür schauen wir uns noch einmal das Beispiel von Herrn Oskar an: Dieses Mal sagt der Arbeitgeber, dass sein Lohn jedes Jahr um $8~\%$ zunimmt. Daraus ergibt sich die folgende Wertetabelle:
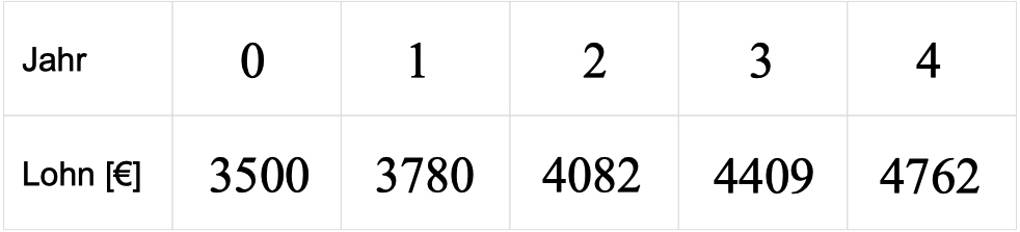
Wenn du umgekehrt eine solche Tabelle vorliegen hast und entscheiden sollst, ob lineares oder exponentielles Wachstum vorliegt, kannst du die Differenzen sowie die Quotienten zweier aufeinanderfolgender Größen untersuchen. Hier beschränken wir uns auf die Quotienten:
- Wert im Jahr $1$ geteilt durch Wert im Jahr $0$: $3780~\text{€}:3500~\text{€}=1,08$
- Wert im Jahr $2$ geteilt durch Wert im Jahr $1$: $4082~\text{€}:3780~\text{€}\approx 1,08$
- Wert im Jahr $3$ geteilt durch Wert im Jahr $2$: $4409~\text{€}:4082~\text{€}\approx 1,08$
Du siehst, der Quotient ist immer (ungefähr) gleich.
Du kannst dieses Verhalten ebenfalls in einem Koordinatensystem darstellen:

Wenn du die Punkte miteinander verbindest, erhältst du den Funktionsgraphen einer Exponentialfunktion. In diesem Beispiel ist diese gegeben durch $f$ mit $f(x)=3500\cdot 1,08^{x}$.
Auch hier kannst du zusammenfassend feststellen:
- Aufeinanderfolgende Werte unterscheiden sich immer um den gleichen Faktor.
- Die Darstellung in einem Koordinatensystem sieht wie folgt aus:

- Die zugehörige Funktionsgleichung ist eine Exponentialfunktion.
Alle Videos zum Thema
Videos zum Thema
Abgrenzung lineares und exponentielles Wachstum (3 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Abgrenzung lineares und exponentielles Wachstum (3 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung





 Lineares Wachstum – Überblick
Lineares Wachstum – Überblick
 Exponentielles vs. lineares Wachstum
Exponentielles vs. lineares Wachstum
 Exponentielles oder lineares Wachstum – Wachstumsprozesse zuordnen
Exponentielles oder lineares Wachstum – Wachstumsprozesse zuordnen









