Ähnlichkeitsabbildungen
zentrische Streckung, Kongruenzabbildung, ähnliche Figuren, Drehung, Verschiebung, Spiegelung, www, Seitenverhältnisse, Winkelgrößen
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
Kongruenz und Ähnlichkeit
Um zu verstehen, was Ähnlichkeitsabbildungen sind, klären wir erst einmal einige Begriffe:
Kongruente Figuren
Zwei geometrische Figuren werden kongruent (deckungsgleich) genannt, wenn sie sich gegenseitig komplett abdecken.
Wenn du zum Beispiel zwei Blatt Papier übereinander legst und ein Dreieck ausschneidest, erhältst du schließlich zwei kongruente Dreiecke.
Du kannst nun von den übereinanderliegenden Dreiecken eines parallel verschieben, an einer Achse oder einem Punkt spiegeln oder um einen Winkel drehen. Es bleibt trotzdem deckungsgleich zu dem anderen Dreieck.
Die Abbildungen Verschiebung, Spiegelung sowie Drehung sind Kongruenzabbildungen.
Für Dreiecke gibt es vier Kongruenzsätze. Diese besagen, wie du bei gegebenen Übereinstimmungen von Seiten und/oder Winkeln entscheiden kannst, ob die Dreiecke kongruent zueinander sind.
Ähnliche Figuren
Zwei Figuren, welche zueinander kongruent sind, sind insbesondere auch ähnlich zueinander.
Da du nun weißt, was kongruente Figuren sind, widmen wir uns der Frage: Was sind ähnliche Figuren? Dies schauen wir uns am Beispiel von ähnlichen Dreiecken an.
Eigenschaften ähnlicher Dreiecke
Wenn zwei Dreiecke in ihren drei Winkeln übereinstimmen, sind die Dreiecke ähnlich zueinander. Warum sind die Dreiecke nicht kongruent?
Für alle gleichseitigen Dreiecke gilt, dass alle drei Winkel gleich groß sind, nämlich $60^\circ$. Das bedeutet, dass zwei beliebige gleichseitige Dreiecke sicher ähnlich zueinander sind. Es sind allerdings nicht alle gleichseitigen Dreiecke kongruent zueinander.
Bei ähnlichen Dreiecken gilt neben der Übereinstimmung der drei Winkel auch, dass die Verhältnisse einander entsprechender Seiten immer gleich sind.
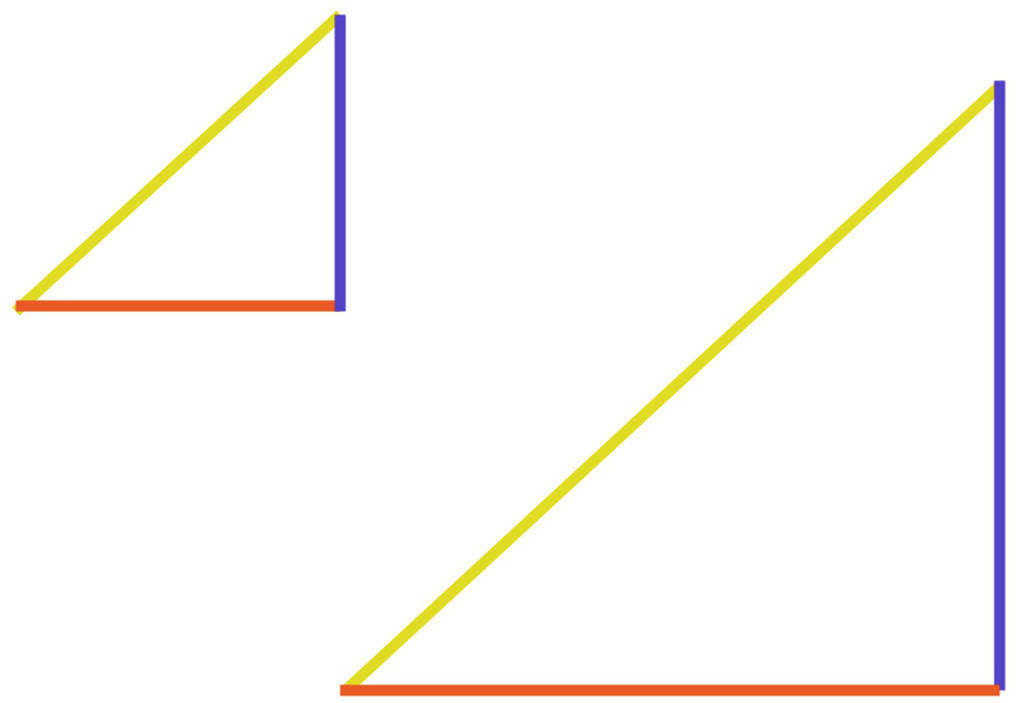
Für die abgebildeten Dreiecke bedeutet dies, dass die Seitenverhältnisse der Seiten mit den gleichen Farben für alle drei Farben immer gleich sind. Diese Dreiecke sind ähnlich.
Was sind Ähnlichkeitsabbildungen?
Ähnlichkeitsabbildungen sind alle Abbildungen, welche eine geometrische Figur auf eine dazu ähnliche Figur abbilden. Insbesondere sind alle Kongruenzabbildungen auch Ähnlichkeitsabbildungen. Es gibt noch eine Abbildung, welche eine Ähnlichkeitsabbildung ist, aber keine Kongruenzabbildung. Dies ist die zentrische Streckung.
Zusammengefasst siehst du hier noch einmal alle Ähnlichkeitsabbildungen:
- Drehung
- Verschiebung
- Spiegelung
- zentrische Streckung
Wenn du zwei oder mehrere dieser Abbildungen hintereinander durchführst, erhältst du wieder eine Ähnlichkeitsabbildung.
Übrigens: Ebenso wie gleichseitige (regelmäßige) Dreiecke immer ähnlich zueinander sind, sind auch regelmäßige Vierecke, also Quadrate, immer ähnlich zueinander.
Rechtecke sind ähnlich zueinander, wenn die Seitenverhältnisse einander entsprechender Seiten immer gleich sind.
Wenn Quadrate oder Rechtecke zueinander mit dem Faktor $k$ ähnlich sind, gilt, dass der Flächeninhalt sich um $k^{2}$ ändert.
Zentrische Streckung
Für eine zentrische Streckung benötigst du ein Streckzentrum $Z$ sowie einen Streckfaktor $k$.
Zentrische Streckung einer Strecke
- Du verbindest einen Endpunkt der Strecke mit dem Streckzentrum $Z$. Zeichne diese Verbindung über den Endpunkt hinaus.
- Nun misst du den Abstand vom Streckzentrum zu diesem Endpunkt. Diesen Abstand multiplizierst du mit dem Streckfaktor $k$.
- Trage eine Strecke der so erhaltenen Länge entlang der Verbindung aus 1. ab. So erhältst du den Bildpunkt des Endpunktes.
Ebenso gehst du bei dem anderen Endpunkt vor.
In dem Bild siehst du die gestreckte Strecke $\overline{AB}$ für verschiedene Streckfaktoren.
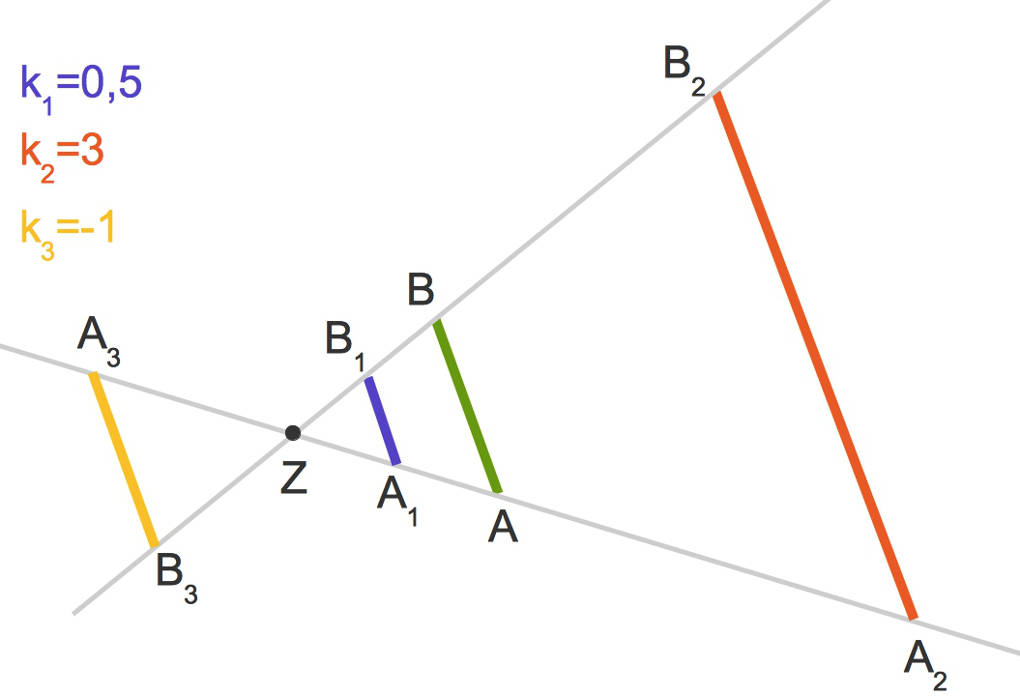
Zentrische Streckung eines Dreiecks
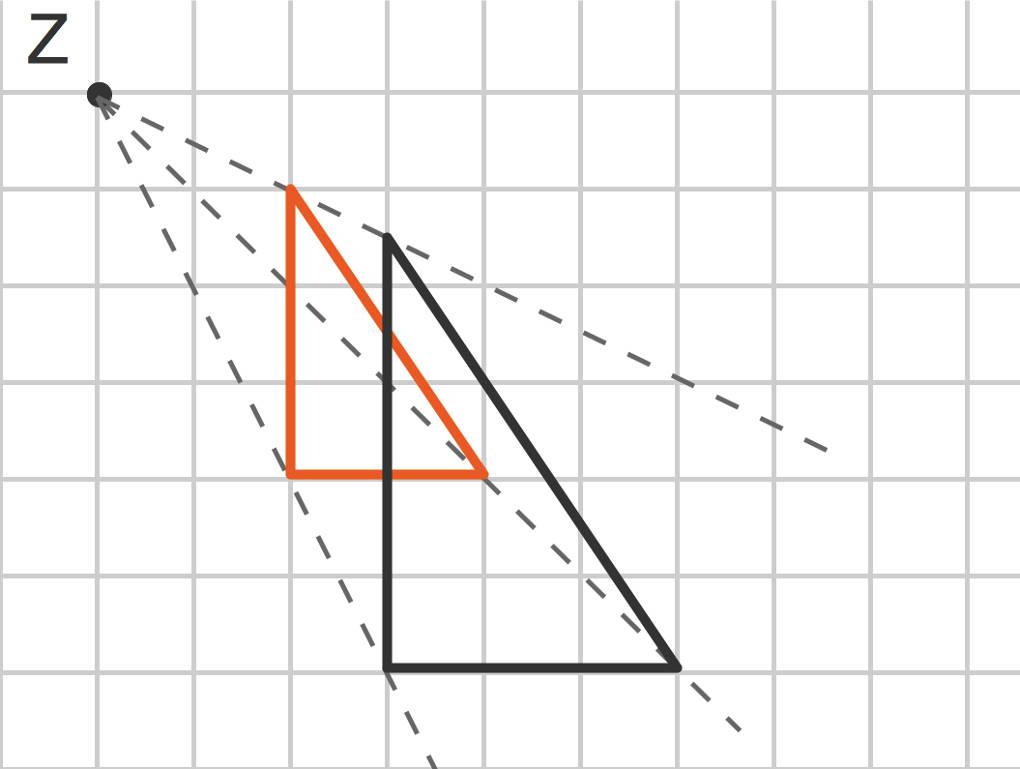
Möchtest du nun ein Dreieck zentrisch strecken, gehst du ebenso vor wie oben beschrieben. Den Vorgang wiederholst du für jeden der drei Eckpunkte. Schließlich verbindest du die so gewonnenen Bildpunkte der Eckpunkte zu dem Bilddreieck.
Alle Videos zum Thema
Videos zum Thema
Ähnlichkeitsabbildungen (8 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Ähnlichkeitsabbildungen (8 Arbeitsblätter)
-
 Eigenschaften ähnlicher Dreiecke
PDF anzeigen
Eigenschaften ähnlicher Dreiecke
PDF anzeigen -
 Ähnlichkeitsabbildungen
PDF anzeigen
Ähnlichkeitsabbildungen
PDF anzeigen -
 Ähnlichkeitsabbildungen – Beispiele
PDF anzeigen
Ähnlichkeitsabbildungen – Beispiele
PDF anzeigen -
 Ähnlichkeitssätze für Dreiecke
PDF anzeigen
Ähnlichkeitssätze für Dreiecke
PDF anzeigen -
 Ähnlichkeitssätze für Dreiecke – Beispiel (1)
PDF anzeigen
Ähnlichkeitssätze für Dreiecke – Beispiel (1)
PDF anzeigen -
 Ähnlichkeitssätze für Dreiecke – Beispiel (2)
PDF anzeigen
Ähnlichkeitssätze für Dreiecke – Beispiel (2)
PDF anzeigen -
 Ähnlichkeitssätze für Dreiecke – Übungen (1)
PDF anzeigen
Ähnlichkeitssätze für Dreiecke – Übungen (1)
PDF anzeigen -
 Ähnlichkeitssätze für Dreiecke – Übungen (2)
PDF anzeigen
Ähnlichkeitssätze für Dreiecke – Übungen (2)
PDF anzeigen
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung



















