Dreiecke – Kongruenzsätze und Konstruktionen
Die Kongruenzsätze geben an, unter welchen Voraussetzungen zwei Dreiecke kongruent, das heißt deckungsgleich, sind. Du kannst diese Sätze aber auch nutzen, um ein Dreieck (eindeutig!) zu konstruieren.
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Dreiecke konstruieren
- Rechtwinklige Dreiecke konstruieren
- Gleichschenklige und gleichseitige Dreiecke konstruieren
Dreiecke konstruieren
Um ein Dreieck zu konstruieren, benötigst du drei Punkte, die nicht alle auf einer Geraden liegen. Verbindest du diese miteinander, so erhältst du ein Dreieck. Dabei sind die drei Punkte die Ecken und die Verbindungsstrecken die Seiten des Dreiecks. So einfach ist das.
Du kannst Dreiecke auch konstruieren, wenn bestimmte Seiten und / oder Winkel gegeben sind. Hierfür verwendest du die Kongruenzsätze.
Wie aber kannst du spezielle Dreiecke konstruieren?
Rechtwinklige Dreiecke konstruieren
Zur Konstruktion eines rechtwinkligen Dreiecks verwendest du den Satz des Thales.
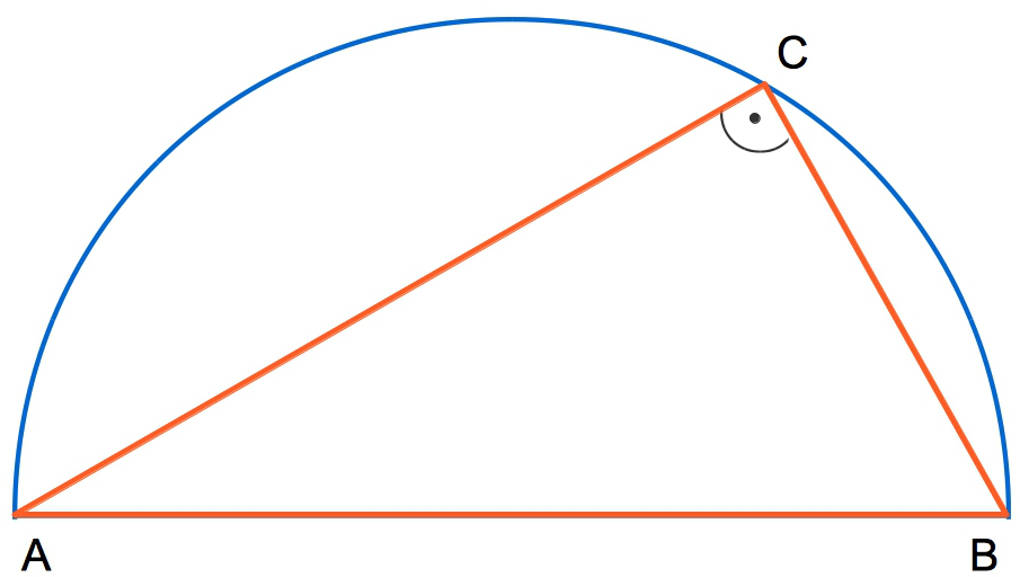
Was besagt dieser Satz? Die Strecke $\overline{AB}$ sei der Durchmesser eines Halbkreises. Wähle nun auf diesem Halbkreis einen beliebigen Punkt $C$. Dann ist das Dreieck $\triangle_{ABC}$ rechtwinklig mit dem rechten Winkel in $C$.
Da bei einem rechtwinkligen Dreieck der Flächeninhalt gerade die Hälfte des Produktes der Kathetenlängen ist, kannst du ein rechtwinkliges Dreieck mit gegebenem Flächeninhalt, zum Beispiel $10~\text{cm}^{2}$, wie folgt konstruieren:
- Wähle die Länge der Katheten so, dass ihr Produkt $2\cdot 10~\text{cm}^2=20~\text{cm}^{2}$ ergibt. Hier wird $4~\text{cm}$ und $5~\text{cm}$ angenommen.
- Zeichne eine Seite der Länge $4~\text{cm}$.
- Errichte in einem der beiden Eckpunkte ein Lot.
- Zeichne nun einen Kreisbogen mit dem Radius $r=5~\text{cm}$ um diesen Eckpunkt.
- Dieser Kreisbogen schneidet das Lot.
- Verbinde diesen Schnittpunkt mit dem anderen Eckpunkt der Ausgangsseite.
- Du hast nun ein rechtwinkliges Dreieck mit dem gegebenen Flächeninhalt konstruiert.
Gleichschenklige und gleichseitige Dreiecke konstruieren
Zunächst einmal klären wir, was eigentlich gleichschenklige und gleichseitige Dreiecke sind:
- In einem gleichschenkligen Dreieck sind mindestens zwei Seiten gleich lang. Diese gleich langen Seiten werden Schenkel genannt. Die verbleibende Seite ist die Basis des Dreiecks. Die beiden an der Basis anliegenden Winkel werden Basiswinkel genannt. Die Basiswinkel sind immer gleich groß.
- In einem gleichseitigen Dreieck sind alle drei Seiten gleich lang. Daraus folgt auch, dass alle drei Winkel gleich groß, nämlich $60^{\circ}$, sind.
Kommen wir nun zur Konstruktion eines gleichschenkligen Dreiecks.
- Zeichne zunächst die Basis.
- Zeichne nun um jeden der beiden Eckpunkte einen Kreisbogen so, dass diese sich schneiden. Wähle hierbei einen Radius, der größer als die Hälfte der Länge der Basis ist.
- Der Schnittpunkt beider Kreisbögen hat zu jedem der beiden Eckpunkte den gleichen Abstand.
- Somit bildet das Dreieck mit den beiden Eckpunkten der Basis sowie dem Schnittpunkt der Kreisbögen ein gleichschenkliges Dreieck.
Wenn du den Radius der Kreisbögen genauso groß wählst wie die Länge der Basis, erhältst du mit der obigen Konstruktion ein gleichseitiges Dreieck.
Übrigens: Ein gleichseitiges Dreieck kannst du auch mit Hilfe eines Kreises konstruieren.
Die vier Kongruenzsätze
Es gibt insgesamt vier Kongruenzsätze. Bevor wir uns diese anschauen, klären wir zunächst, was „kongruent“ eigentlich bedeutet.
Ein anderes Wort für „kongruent“ ist „deckungsgleich“. Wenn du zwei Blatt Papier übereinander legst und dann ein Dreieck ausschneidest, erhältst du mit jedem der Blätter ein solches Dreieck, also zwei Dreiecke. Diese beiden Dreiecke decken sich gegenseitig vollständig ab. Sie sind also deckungsgleich.
Nun weißt du, was kongruent bedeutet. Dann siehst du jetzt die vier Kongruenzsätze:
- Der Kongruenzsatz SSS besagt, dass zwei Dreiecke kongruent zueinander sind, wenn sie in den Längen ihrer drei Seiten übereinstimmen.
- Der Kongruenzsatz SWS besagt, dass zwei Dreiecke kongruent zueinander sind, wenn sie in den Längen zweier Seiten sowie dem von diesen Seiten eingeschlossenen Winkel übereinstimmen.
- Der Kongruenzsatz SSW besagt, dass zwei Dreiecke kongruent zueinander sind, wenn sie in den Längen zweier Seiten sowie dem der längeren der beiden Seiten gegenüberliegenden Winkel übereinstimmen.
- Der Kongruenzsatz WSW besagt, dass zwei Dreiecke kongruent zueinander sind, wenn sie in der Länge einer Seite sowie den beiden an dieser Seite anliegenden Winkeln übereinstimmen.
Du kannst diese Kongruenzsätze auch anwenden, um ein Dreieck eindeutig zu konstruieren.
Verwende im Folgenden diese Planfigur für ein Dreieck:
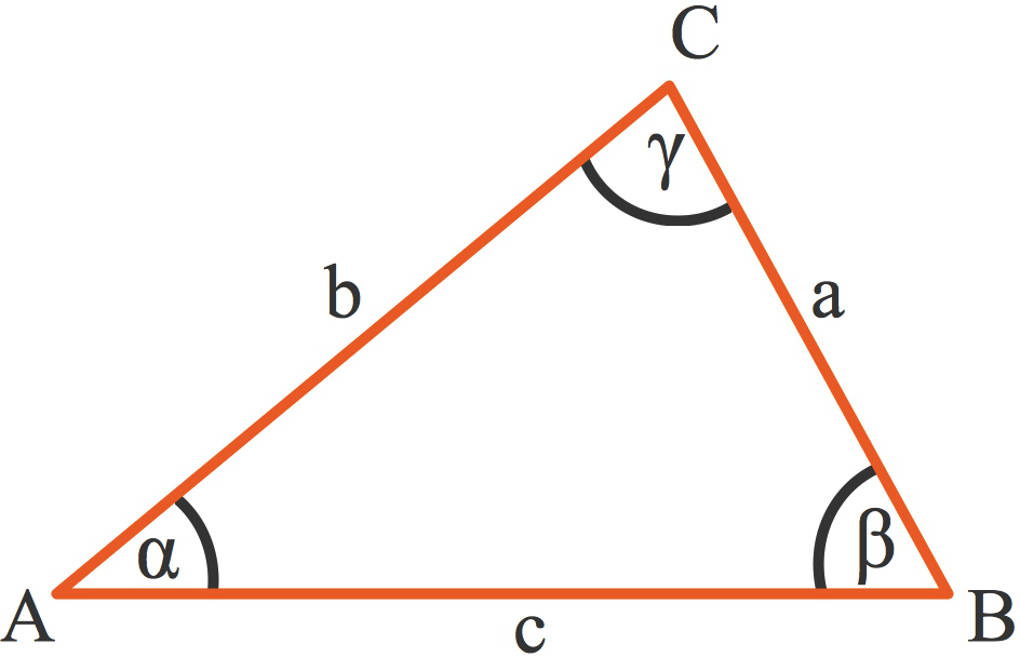
Der Kongruenzsatz SSS
Du kannst ein Dreieck nach SSS konstruieren, wenn alle $3$ Seiten gegeben sind. Zum Beispiel seien $a=5~\text{cm}$, $b=6~\text{cm}$ und $c=8~\text{cm}$. Du gehst dabei wie folgt vor:
- Du zeichnest, zum Beispiel mit dem Geodreieck, eine Seite ein. Es ist dabei egal, mit welcher Seite du beginnst. Wir beginnen einmal mit der Seite $c$, welche die Punkte $A$ und $B$ verbindet.
- Zeichne nun um den Punkt $A$ einen Kreisbogen mit dem Radius $b$.
- Zeichne einen weiteren Kreisbogen, dieses Mal um $B$, mit dem Radius $a$.
- Diese beiden Kreisbögen schneiden sich in zwei Punkten. Wähle einen der beiden Punkte als $C$, den fehlenden Eckpunkt. Du kannst nun sagen, dass du ja zwei Dreiecke erhältst. Diese sind allerdings deckungsgleich.
- Verbinde zuletzt $A$ und $C$, dies ist die Seite $b$, sowie $B$ und $C$ zur Seite $a$.

Fertig ist das Dreieck.
Der Kongruenzsatz SWS
Weiter geht's mit der Konstruktion eines Dreiecks, wenn $2$ Seiten und der eingeschlossene Winkel gegeben sind. Führe doch einmal die Konstruktion auf einem Blatt durch:
- Du zeichnest eine der beiden gegebenen Seiten ein. Es ist auch hier egal, mit welcher Seite du beginnst. Nehmen wir einmal an, du kennst die Seiten $b=7~\text{cm}$ und $c=10~\text{cm}$ sowie den Winkel $\alpha=60^\circ$. Beginne mit der Seite $c$. Diese verbindet die Punkte $A$ und $B$.
- Trage in $A$ den Winkel $\alpha$ an. So erhältst du einen freien Schenkel.
- Zeichne nun um den Punkt $A$ einen Kreisbogen mit dem Radius $b$.
- Der Kreisbogen schneidet den freien Schenkel. Der Schnittpunkt ist der fehlende Eckpunkt $C$
- Verbinde zuletzt $A$ und $C$, dies ist die Seite $b$, sowie $B$ und $C$ zur Seite $a$.
Nun ist auch dieses Dreieck konstruiert.
Der Kongruenzsatz SSW
Nun kommen wir zur Konstruktion eines Dreiecks nach SSW. Das heißt, wenn $2$ Seiten und der der längeren der beiden Seiten gegenüberliegende Winkel gegeben sind . Du kannst auch hier die Konstruktion auf einem Blatt üben. Dieses Mal seien $c=12~\text{cm}$, $b=7~\text{cm}$ sowie $\gamma=80^\circ$ gegeben.
- Zeichne zunächst die kürzere der beiden Seiten. Diese ist in diesem Beispiel die Seite $b$, welche die Punkte $A$ und $C$ verbindet.
- Trage in $C$ den Winkel $\gamma$ an. So erhältst du einen freien Schenkel.
- Zeichne nun um den Punkt $A$ einen Kreisbogen mit dem Radius $c$.
- Der Kreisbogen schneidet den freien Schenkel. Der Schnittpunkt ist der fehlende Eckpunkt $B$.
- Verbinde zuletzt $A$ und $B$, dies ist die Seite $c$, sowie $B$ und $C$ zur Seite $a$.
Wichtig: Wenn der Winkel der kürzeren der beiden Seiten gegenüberliegt, erhältst du zwei Dreiecke, welche nicht kongruent zueinander sind. Das bedeutet, dass das Dreieck in diesem Fall nicht eindeutig konstruierbar ist.
Der Kongruenzsatz WSW
Es bleibt noch ein Kongruenzsatz: Du konstruierst ein Dreieck, wenn $1$ Seite sowie die beiden anliegenden Winkel gegeben sind (WSW). Übung macht den Meister: Du kannst auch diese Konstruktion selbst auf einem Blatt durchführen. Dieses Mal seien $c=12~\text{cm}$, $\alpha=40^{\circ}$ sowie $\beta=60^{\circ}$ gegeben.
- Zeichne zunächst die gegebene Seite $c$ mit den Endpunkten $A$ und $B$ ein.
- Trage in $A$ den Winkel $\alpha$ an. So erhältst du einen freien Schenkel.
- Trage in $B$ den Winkel $\beta$ an. So erhältst du einen weiteren freien Schenkel.
- Die beiden freien Schenkel schneiden sich in dem fehlenden Eckpunkt $C$.
- Verbinde zuletzt $A$ und $C$ zur Seite $b$ sowie $B$ und $C$ zur Seite $a$.
Geschafft!
Alle Videos zum Thema
Videos zum Thema
Dreiecke – Kongruenzsätze und Konstruktionen (16 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Dreiecke – Kongruenzsätze und Konstruktionen (16 Arbeitsblätter)
-
 Kongruenzsätze für Dreiecke – Überblick
PDF anzeigen
Kongruenzsätze für Dreiecke – Überblick
PDF anzeigen -
 Kongruenzsätze – SSS
PDF anzeigen
Kongruenzsätze – SSS
PDF anzeigen -
 Kongruenzsätze – WSW
PDF anzeigen
Kongruenzsätze – WSW
PDF anzeigen -
 Kongruenzsätze – SWS
PDF anzeigen
Kongruenzsätze – SWS
PDF anzeigen -
 Kongruenzsätze – SSW
PDF anzeigen
Kongruenzsätze – SSW
PDF anzeigen -
 Dreiecke konstruieren – Kongruenzsatz SsW
PDF anzeigen
Dreiecke konstruieren – Kongruenzsatz SsW
PDF anzeigen -
 Dreiecke konstruieren – Bedingungen für Seiten und Winkel
PDF anzeigen
Dreiecke konstruieren – Bedingungen für Seiten und Winkel
PDF anzeigen -
 Gleichschenklige und gleichseitige Dreiecke konstruieren
PDF anzeigen
Gleichschenklige und gleichseitige Dreiecke konstruieren
PDF anzeigen -
 Die Höhe eines Dreiecks
PDF anzeigen
Die Höhe eines Dreiecks
PDF anzeigen -
 Inkreis und Umkreis von Dreiecken – Überblick
PDF anzeigen
Inkreis und Umkreis von Dreiecken – Überblick
PDF anzeigen -
 Mittelpunkt eines Kreises konstruieren
PDF anzeigen
Mittelpunkt eines Kreises konstruieren
PDF anzeigen -
 Die Mittelsenkrechte
PDF anzeigen
Die Mittelsenkrechte
PDF anzeigen -
 Die Winkelhalbierende
PDF anzeigen
Die Winkelhalbierende
PDF anzeigen -
 Die Seitenhalbierende
PDF anzeigen
Die Seitenhalbierende
PDF anzeigen -
 Mittelpunkt einer Strecke und Schwerpunkt eines Dreiecks
PDF anzeigen
Mittelpunkt einer Strecke und Schwerpunkt eines Dreiecks
PDF anzeigen -
 Dreiecke aus gegebenen Angaben zeichnen
PDF anzeigen
Dreiecke aus gegebenen Angaben zeichnen
PDF anzeigen
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung



























