Parabelscharen


in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Grundlagen zum Thema Parabelscharen
Dieses Video beschäftigt sich mit Parabelscharen. Das heißt, wir schauen uns an, welchen Einfluss die Parameter a, b und c auf die Parabel der Form f(x)=ax² +bx+c haben und welche Besonderheiten es gibt. Außerdem sehen wir uns in diesem Video gemeinsam an, wie man die Ortskurve einer Parabelschar bestimmt. Viel Spaß!
Transkript Parabelscharen
Hallo! Ich bin Aline und dieses Video beschäftigt sich mit Parabelscharen. Parabelscharen, was ist das überhaupt? Du kennst bereits die allgemeine Form einer Parabel, f(x) = ax² + bx + c. Abhängig von den Parametern a, b und c unterscheiden sich die einzelnen Parabeln. Sie können auf der x-Achse oder der y-Achse verschoben oder gestaucht, beziehungsweise gestreckt sein. Wir sprechen von einer Parabelschar, wenn mindestens einer der drei Parameter nicht eindeutig bestimmt ist und somit unendlich viele Parabeln zu derselben Funktion existieren. Doch schauen wir uns dies nun genauer an, indem wir zunächst noch einmal die allgemeine Parabelform wiederholen und uns danach die Parabelscharen anschauen für die Fälle, dass entweder a und b gegeben oder b und c gegeben oder a und c gegeben sind. Die allgemeine Parabelform lautet wie folgt: f(x) = ax² + bx + c. a, b und c sind unsere veränderlichen Parameter und bestimmen das Aussehen der Parabel. a, b und c sind Elemente der reellen Zahlen, allerdings mit einer Ausnahme, a darf nicht 0 werden, da sonst der Term ax² 0 wird und es sich dann nicht mehr um eine Parabel handelt. Wir können also sagen, dass b und c Element R sind, a jedoch Element R{0} ist. Was passiert nun mit einer Parabel, wenn a und b festgelegt sind, c jedoch veränderlich ist. Nehmen wir zum Beispiel die Gleichung g(x) = 2x² + 3x + c und setzen für c 0, 2 und -1 ein. Dann erkennen wir, dass der Graph der y-Achse verschoben wird. Wir können also festhalten, dass c uns den Schnittpunkt mit der y-Achse angibt und, dass über eine Veränderung der Werte für c der Graph vertikal verschoben wird. Sind b und c festgelegt und a veränderlich, erhalten wir andere Parabelscharen. Setzen wir in die Funktion h(x) = ax² + x + 1 verschiedene Werte für a ein, sehen wir, dass die Funktion gestaucht, beziehungsweise gestreckt wird und nach oben oder unten geöffnet ist. Setzen wir für a 1 ein, dann ergibt sich die Standardform. Ist a größer als 1 oder kleiner -1 wird die Funktion gestreckt. Nehmen wir zum Beispiel a = 2, wird die Kurve schmaler im Vergleich zur Standardform. Ist a kleiner als 1 und größer als -1, wird die Funktion gestaucht. Dies sieht man bei a = 0,5. Dort ist die Funktion breiter als bei der Standardform. Ist a positiv, ist die Parabel nach oben geöffnet. Ist a negativ, ist die Parabel nach unten geöffnet. Bei veränderlichem a können wir innerhalb der Parabelschar einen Fixpunkt ausmachen. Dies ist der Schnittpunkt mit der y-Achse, den alle Graphen der Schar gemein haben. In dem letzten Fall schauen wir uns an was passiert, wenn a und c festgelegt sind und b veränderlich ist. Ist in der Funktion i(x) = x² + bx + 1, b = 0, dann liegt der Scheitelpunkt direkt auf der y-Achse. Für b > 0 wird die Kurve nach links und nach unten verschoben und ist b < 0, verschiebt sich der Graph nach rechts und nach unten. Der Parameter b ist also dafür zuständig, die Kurve und damit auch die Scheitelpunkte, sowohl auf der x-Achse, als auch auf der y-Achse, zu verschieben. Alle Scheitelpunkte dieser Parabelschar liegen auf einer gemeinsamen Kurve, der sogenannten Ortskurve. Die Ortskurve bestimmt man, indem man (1) die erste und zweite Ableitung der Funktion bildet, (2) die erste Ableitung mit 0 gleichsetzt, dann (3) mit der zweiten Ableitung prüft, ob es sich um eine Extremstelle handelt, (4) den x-Wert der Extremstelle in die Ausgangsfunktion einsetzt und den dazugehörigen y-Wert bestimmt, (5) den x-Wert des Extrempunkts von b umstellt und schließlich (6) b in den y-Wert des Extrempunkts einsetzt. Für unser Beispiel i(x) = x² + bx + 1 können wir die Ortskurve wie folgt bilden. Wir bilden zunächst die erste Ableitung und erhalten i'(x) = 2x + b. Um die Extremstelle berechnen zu können, müssen wir die erste Ableitung mit 0 gleichsetzen. Wir erhalten x = -b/2. Mit der zweiten Ableitung prüfen wir, ob es sich um eine Extremstelle handelt. Die zweite Ableitung lautet i''(x) = 2. Damit handelt es sich bei x = -b/2 um eine Extremstelle, da 2 ungleich 0 ist. Um den y-Wert der Extremstelle zu erhalten, setzen wir in die Funktion i(x) den x-Wert -b/2 ein und erhalten y = i(-b/2) = (-b/2)² + b(-b/2) + 1. Das ergibt y = -b²/4 + 1. Der Extrempunkt liegt also bei PE(-b/2; -b²/4 + 1). Nun stellen wir den x-Wert nach b um und erhalten b = -2x und setzen dies in den y-Wert für b ein. Es ergibt sich die Ortskurve y = -(-2x)²/4 + 1 und zusammengefasst ist das y = -x² + 1. In diesem Video haben wir uns mit Parabelscharen beschäftigt und uns angeschaut, wie die einzelnen Parameter a, b und c der Funktion f(x) = ax² + bx + c die Lage und Form der Funktion beeinflussen. Wir haben festgestellt, dass a die Form der Funktion verändert, b die Funktion auf der x-Achse und c die Funktion auf der y-Achse verschiebt. Außerdem haben wir kennengelernt, wie man die Ortskurve einer Parabelschar bestimmt, welche den Verlauf der Scheitelpunkte abbildet. Hoffentlich bist du nun schon viel sicherer im Umgang mit Parabelscharen. Tschüss und bis zum nächsten Mal.
Parabelscharen Übung
-
Benenne die einzelnen Schritte zur Bestimmung einer Ortskurve der Extrema.
TippsEs ist nicht sinnvoll, einen Extrempunkt zu berechnen, wenn man nicht vorher geprüft hat, ob wirklich ein Extrempunkt vorliegt.
Die ersten Schritte sind die, die du bereits vom Ermitteln von Extrempunkten kennst.
Bei Parabelscharen hängen die Koordinaten gegebenenfalls von dem Scharparameter ab.
LösungWenn zum Beispiel $a$ und $c$ fest sind und der Parameter $b$ veränderlich, dann kommt man zu Extrema, die von dem Parameter $b$ abhängen. Diese Extrema liegen auf einer Kurve, der sogenannten Ortskurve der Extrema.
Es sind die folgenden Schritte durchzuführen, um eine solche Ortskurve zu bestimmen. (Übrigens: Diese Schritte sind unabhängig von der Funktionsklasse. Das bedeutet, dass sie nicht nur auf quadratische Funktionen anwendbar sind.)
- Für die Extrema benötigt man die 1. und 2. Ableitung.
- Es muss die Gleichung $f'(x)=0$ gelöst werden. Dies ist die notwendige Bedingung.
- Mit der zweiten Ableitung wird geprüft, ob es sich tatsächlich um eine Extremstelle handelt.
- Durch Einsetzen des x-Wertes aus Schritt 2 in die Funktionsgleichung erhält man die y-Koordinate des Extremums. Dies ist bei einer Parabel der Scheitelpunkt.
- Der x-Wert wird nach dem Parameter $b$ umgestellt.
- Dieser Parameter wird in der y-Koordinate eingesetzt.
-
Bestimme die Ortskurve der Extrema für die Funktion $i(x)=x^2+bx+1$.
TippsDies sind die einzelnen Schritte:
- 1. und 2. Ableitung bestimmen.
- 1. Ableitung gleich $0$ lösen.
- Mit der zweiten Ableitung wird geprüft, ob es sich tatsächlich um eine Extremstelle handelt.
- Einsetzen des x-Wertes aus Schritt 2 in die Funktionsgleichung. Dies führt zu der y-Koordinate des Scheitelpunktes.
- Der x-Wert wird nach dem Parameter $b$ umgestellt.
- Dieser Parameter wird in die y-Koordinate eingesetzt.
Verwende die Potenzregel zum Ableiten der Funktion.
Zum Beispiel sind die ersten beiden Ableitungen von $f(x)=ax^2+bx+c$ gegeben durch
- $f'(x)=2ax+b$ sowie
- $f''(x)=2a$.
Da der Graph eine Parabel ist, ist das hinreichende Kriterium auf jeden Fall erfüllt.
LösungUm die Ortskurve der Extrema (Scheitelpunkte) zu bestimmen, muss zunächst die Funktion auf Extrema untersucht werden.
Hierfür werden die ersten beiden Ableitungen benötigt:
- $i'(x)=2x+b$ sowie
- $i''(x)=2$
$x=-\frac b2$.
Ob wirklich ein Extremum vorliegt, kann man durch Einsetzen dieses x-Wertes in die 2. Ableitung prüfen:
$i''\left(-\frac b2\right)=2\neq 0$.
Es liegt also ein Extremum (hier: Scheitelpunkt) vor. Da die Parabel nach oben geöffnet ist, ist es ein Tiefpunkt. Um die y-Koordinate des Scheitelpunktes zu erhalten, wird $x=-\frac b2$ in die Funktionsgleichung eingesetzt:
$i\left(-\frac b2\right)=\left(-\frac b2\right)^2+b\left(-\frac b2\right)+1=\frac{b^2}{4}-\frac{b^2}2+1=-\frac{b^2}4+1$.
Es hängen also sowohl die x- als auch die y-Koordinate des Scheitelpunktes von dem Parameter $b$ ab.
Nun wird die x-Koordinate nach diesem Parameter umgestellt
$\begin{array}{rclll} x&=&-\frac b2&|&\cdot (-2)\\ -2x&=&b \end{array}$
Zuletzt wird dieses $b$ in die y-Koordinate des Scheitelpunktes eingesetzt und man erhält
$y(x)=-\frac{(-2x)^2}4+1=-\frac{4x^2}4+1=-x^2+1$.
Dies ist die gesuchte Ortskurve der Scheitelpunkte.
-
Bestimme die Scheitelpunkte der Funktionen.
TippsDie x-Koordinate ist immer die Hälfte des Faktors vor dem $x$ mit umgekehrtem Vorzeichen, dividiert durch $a$, den Faktor vor dem $x^2$.
Die y-Koordinate des Scheitelpunktes erhältst du, indem du die x-Koordinate in die Funktionsgleichung einsetzt.
Natürlich kannst du auch die Gleichung $f'(x)=0$ lösen. Dies führt zu der gleichen x-Koordinate.
Ist die Funktion in der Scheitelpunktform $f(x)=a(x-d)^2+e$ gegeben, dann ist der Scheitelpunkt $S(d|e)$.
LösungDie obere der beiden Funktionsgleichungen ist eine quadratische Gleichung in der allgemeinen Darstellung, die untere die Scheitelpunktform.
In beiden sind Parameter vorhanden. Diese Parameter haben einen Einfluss auf die Lage des Funktionsgraphen, der Parabel.
Der tiefste oder höchste Punkt einer Parabel (je nach Öffnung) ist der Scheitelpunkt. Das heißt, dass man an diesem Punkt die Lage fest machen kann.
Bei der Scheitelpunktform kann man den Scheitelpunkt $S(d|e)$ direkt ablesen. Bei der allgemeinen Darstellung ist
- die x-Koordinate des Scheitelpunktes gegeben durch $x=-\frac b{2a}$ und
- die y-Koordinate erhält man durch Einsetzen der x-Koordinate in die Funktionsgleichung.
Schauen wir uns die verschiedenen Funktionsgleichungen genauer an:
- Der Scheitelpunkt der Funktion $f(x)=2(x-2)^2+3$ ist $S(2|3)$.
- $g(x)=x^2+4x+c$: Hier ist $g'(x)=2x+4$ und $g''(x)=2$. Die x-Koordinate des Scheitelpunktes ist $x=-2$. Diese wird in $g(x)$ eingesetzt und man erhält $g(-2)=(-2)^2+4(-2)+c=4-8+c=-4+c$.
- $h(x)=-x^2+2x-1=-(x^2-2x+1)=-(x+1)^2$. Dies ist die 1. binomische Formel. Damit ist $S(-1|0)$.
- $k(x)=\frac12x^2+bx$ hat die ersten beiden Ableitungen $k'(x)=x+b$ sowie $k''(x)=1\neq 0$. Es muss $k'(x)=0$ gelten. Dies führt zu $x=-b$. Wenn man dieses $x$ in die Funktionsgleichung einsetzt, erhält man $k(-b)=\frac12(-b)^2+b(- b)=\frac12 b^2-b^2=-\frac12 b^2$. Damit ist der Scheitelpunkt $S\left(-b|-\frac2 b^2\right)$.
-
Leite die Ortskurve der Scheitelpunkte her.
TippsWenn der Scheitelpunkt bereits bekannt ist, kann man die Ortkurve ausschließlich mit diesem Punkt bestimmen.
Die Ortskurve gibt einen Zusammenhang zwischen der y-Koordinate des Scheitelpunktes sowie dessen x-Koordinate wieder.
Die Ortskurve, auf der diese Punkte liegen, lässt sich wie folgt bestimmen:
- $x=2b$ $\Leftrightarrow$ $b=\frac x2$
- $y(x)=4\cdot \frac x2+1=2x+1$
LösungDie Funktion $k(x)=\frac12x^2+bx$ hat die hier zu sehenden Scheitelpunkte in Abhängigkeit des Parameters $b$.
Zunächst wird die x-Koordinate nach $b$ umgeformt. Hierfür wird die Gleichung $x=-b$ mit $-1$ multipliziert: Dies führt zu $b=-x$.
Dieses $b$ wird in die y-Koordinate eingesetzt:
$y(x)=-\frac{(-x)^2}2=-\frac{x^2}2$.
Dies ist die gesuchte Ortskurve.
Wenn man diese Kurve in ein x-y-Koordinatensystem einzeichnet, erkennt man, dass alle Scheitelpunkte der Parabelschar auf dieser Kurve liegen. Umgekehrt kann man zu einer beliebigen Funktion der Parabelschar mit Hilfe der Ortskurve den Scheitelpunkt angeben.
-
Beschreibe die Bedeutung des Parameters $c$ auf die Parabeln der Funktion: $f(x)=x^2+x+c$.
TippsWenn du die Nullstellen einer Funktion berechnen musst, löst du die Gleichung $f(x)=0$.
Wenn du wissen willst, wo die Funktion die y-Achse schneidet, setzt du $x=0$ in die Funktionsgleichung ein.
Dies ist der Graph der Funktion $f(x)=x^2-2$.
Wenn eine Funktion der Form $f(x)=ax^2+bx+c$ den hier abgebildeten Funktionsgraphen beschreibt, so ist $c=2$.
Erstelle eine Wertetabelle für verschiedene $c$. Was fällt dir auf?
LösungBei dieser Funktion ist $a=b=1$ und $c$ veränderbar. Welchen Einfluss hat $c$ auf die Parabel?
Wenn man $x=0$ in die Funktionsgleichung einsetzt, erhält man
$f(0)=0^2+0+c=c$.
Das bedeutet, dass die Parabel bei $c$ die y-Achse schneidet. Denn da, wo der Schnittpunkt mit der y-Achse stattfindet, muss $x=0$ gelten.
Weiter kann man daraus herleiten, dass positive $c$ zu einer Verschiebung der Parabel nach oben führen. Negative $c$ führen zu einer Verschiebung nach unten.
-
Bestimme die Scheitelpunkte der Parabelschar sowie deren Ortskurve.
TippsForme die x-Koordinate des Scheitelpunktes nach $b$ um.
Dies führt zu $b=\frac x2$.
Setze dieses $b$ in die y-Koordinate des Scheitelpunktes ein.
LösungEs soll die Ortskurve der Extrema (hier: Scheitelpunkte) bestimmt werden. Hierfür werden zunächst die ersten beiden Ableitungen der Funktion benötigt:
- $f'(x)=-\frac12x+b=-0,5x+b$
- $f''(x)=-\frac12$
$\begin{array}{rclll} -\frac12x+b&=&0&|&+\frac12x\\ b&=&\frac12x&|&\cdot 2\\ 2b&=&x \end{array}$
Dieses $x=2b$ wird in die Funktionsgleichung eingesetzt:
$y=f(2b)=-\frac14(2b)^2+b(2b)+1=-b^2+2b^2+1=b^2+1$.
Der Scheitelpunkt lautet also $S(2b|b^2+1)$.
Die x-Koordinate wird nach dem Parameter umgeformt: Hierfür wird durch $2$ dividiert. Dies führt zu $b=\frac x2$.
Dieses $b$ wird in die y-Koordinate eingesetzt:
$y(x)=\left(\frac x2\right)^2+1=\frac{x^2}4+1=0,25 x^2+1$.
Dies die gesuchte Gleichung der Ortskurve.

Ortskurve (Ortslinie) bei Parabelscharen – Beispiele
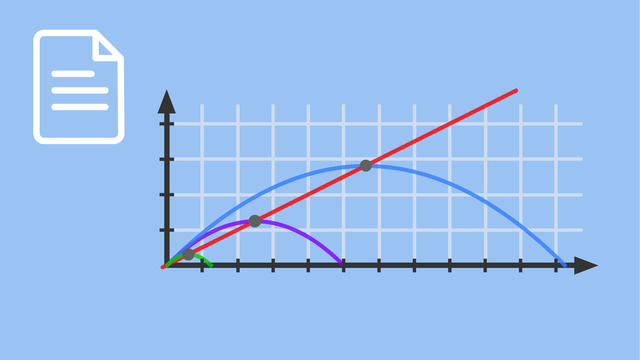
Ortskurve (Ortslinie) bei ganzrationalen Funktionen

Parabelscharen

Parabelscharen – Beispiele

Scharen von Wurzelfunktionen – Kurvendiskussion

Scharen von Exponentialfunktionen – Kurvendiskussion (1)

Scharen von Exponentialfunktionen – Kurvendiskussion (2)

Scharen von Logarithmusfunktionen – Kurvendiskussion

Schar von Winkelfunktionen – Kurvendiskussion
9.926
sofaheld-Level
6.600
vorgefertigte
Vokabeln
7.800
Lernvideos
37.172
Übungen
32.630
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Schulstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung




 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?









Super Video ;)