Funktionen transformieren, verschieben, strecken

Inhaltsverzeichnis zum Thema

• Was ist eine Transformation?
• Die Verschiebung eines Funktionsgraphen
  • Verschiebung entlang der x-Achse
  • Verschiebung entlang der y-Achse
• Die Streckung oder Stauchung sowie Spiegelung eines Funktionsgraphen
• Funktionsgraphen mit dem Parameterverfahren verschieben
• Die Addition von Funktionsgleichungen
• Die Verknüpfung von Funktionsgleichungen
  • Beispiel 1
  • Beispiel 2

Was ist eine Transformation?

Im Folgenden wird an dem Beispiel der Normalparabel $f(x)=x^2$ gezeigt, in welcher Form der zugehörige Funktionsgraph transformiert, das heißt, verändert werden kann.

$~~~$

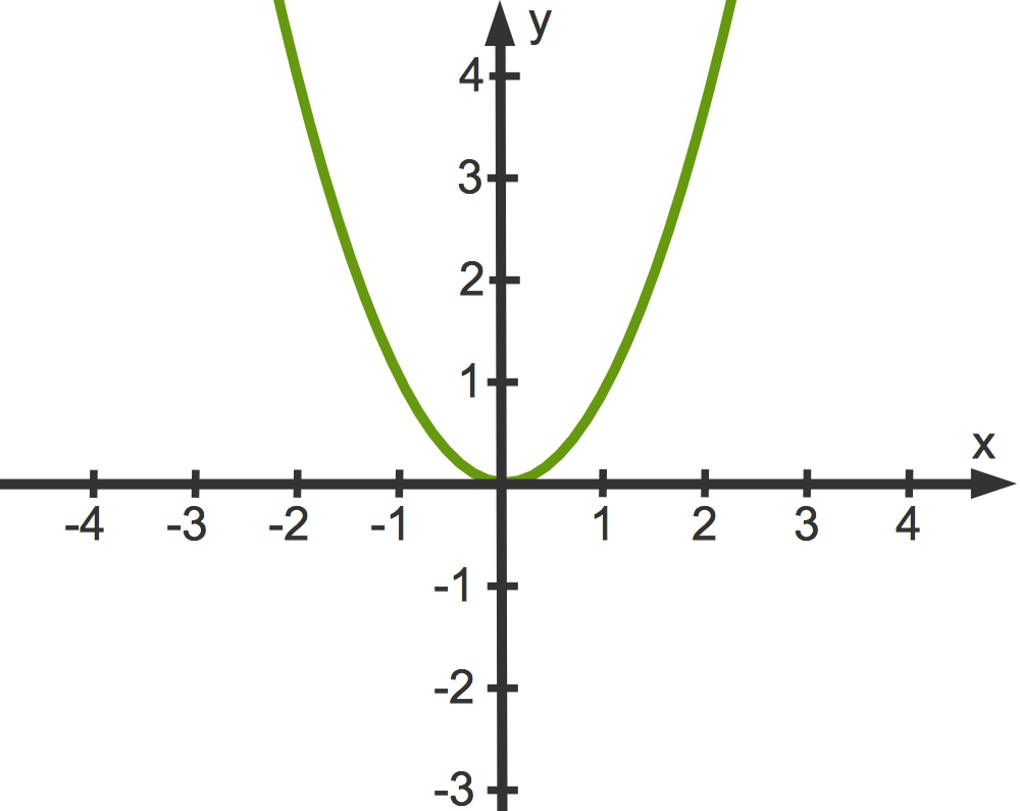
Eine Transformation ist also eine Veränderung. Du wirst sehen, welche Auswirkung eine Veränderung der Funktionsgleichung auf den Funktionsgraphen hat:

• Der Funktionsgraph kann innerhalb des Koordinatensystems verschoben werden.
• Der Funktionsgraph kann auch gestreckt oder gestaucht werden.
• Der Funktionsgraph kann gespiegelt werden.
• Es können auch Funktionsgleichungen addiert oder miteinander verknüpft werden.

Die allgemeine Gleichung einer quadratischen Funktion sieht so aus:

$q(x)=ax^2+bx+c$

oder in Scheitelpunktform mit dem Scheitelpunkt $S(x_S|y_s), so:$

$q(x)=a(x-x_s)^2+y_s$.

Der Graph einer quadratischen Funktion ist eine Parabel. Jede Parabel geht aus der Normalparabel zu $f(x)=x^2$ durch Verschiebung und / oder Streckung beziehungsweise Stauchung sowie gegebenenfalls Spiegelung hervor.

Die Verschiebung eines Funktionsgraphen

Die beiden Parameter der quadratischen Funktion $b$ und $c$ bewirken eine Verschiebung der Parabel des Funktionsgraphen entlang der Koordinatenachsen.

Man kann entweder einzelne Punkte der Parabel verschieben oder die gesamte Parabel parallel verschieben.

Diese kann man sich am besten an der Scheitelpunktform $q(x)=a(x-x_s)^2+y_s$ klarmachen.

Verschiebung entlang der x-Achse

Eine quadratische Funktion $q(x)=(x-x_s)^2$ hat eine Parabel als Funktionsgraphen, die durch Verschiebung der Normalparabel entlang der x-Achse entsteht.

• $q(x)=(x-2)^2$ führt zu einer Verschiebung um $2$ Längeneinheiten in positiver x-Achsen-Richtung. Der Scheitelpunkt ist $S(2|0)$.

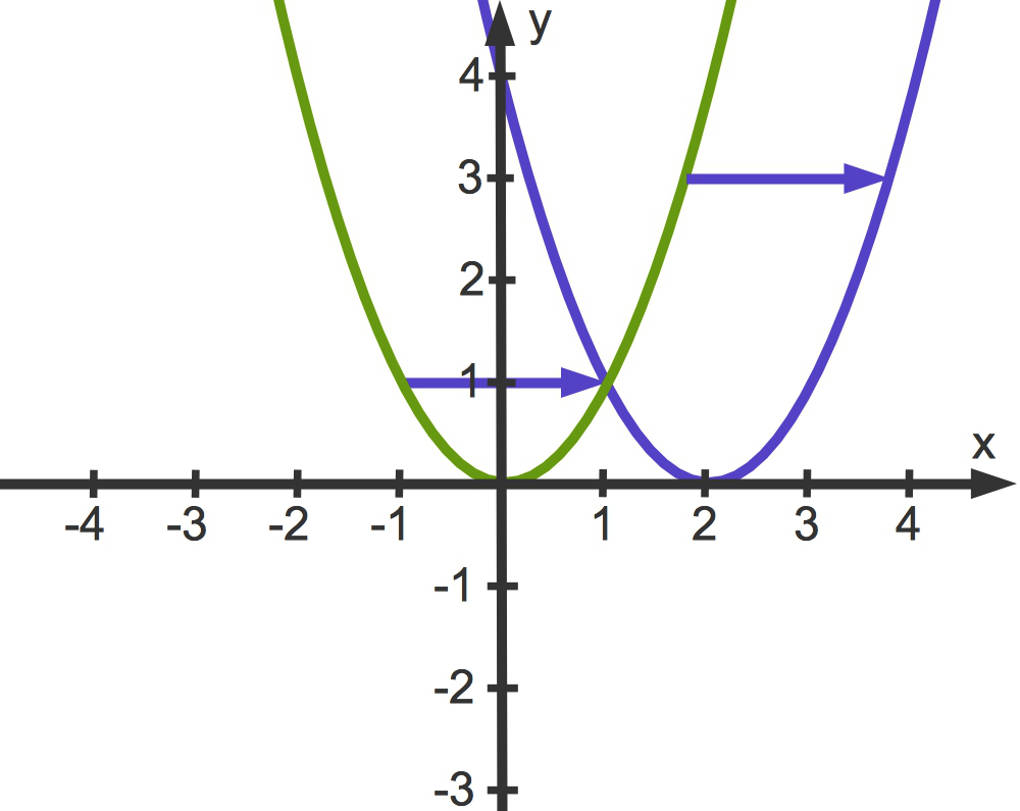
• $q(x)=(x+3)^2$ führt zu einer Verschiebung um $3$ Längeneinheiten in negativer x-Achsen-Richtung. Der Scheitelpunkt ist $S(-3|0)$.

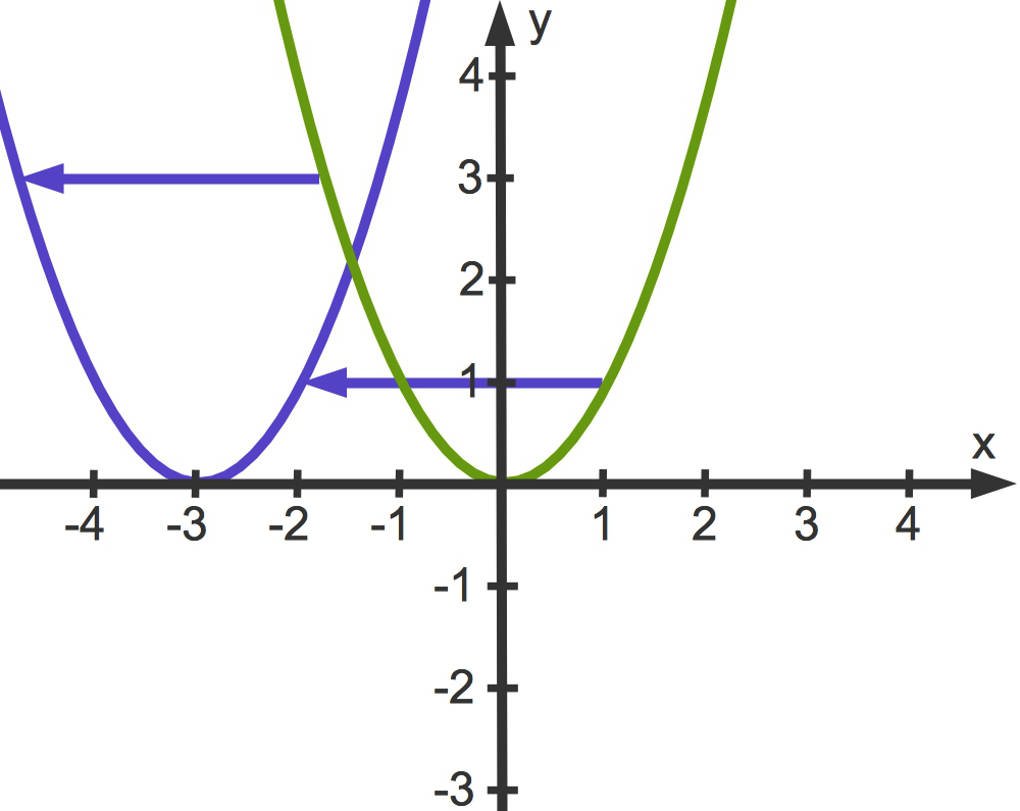
Verschiebung entlang der y-Achse

Eine quadratische Funktion $q(x)=x^2+y_s$ hat eine Parabel als Funktionsgraphen, die durch Verschiebung der Normalparabel entlang der y-Achse entsteht.

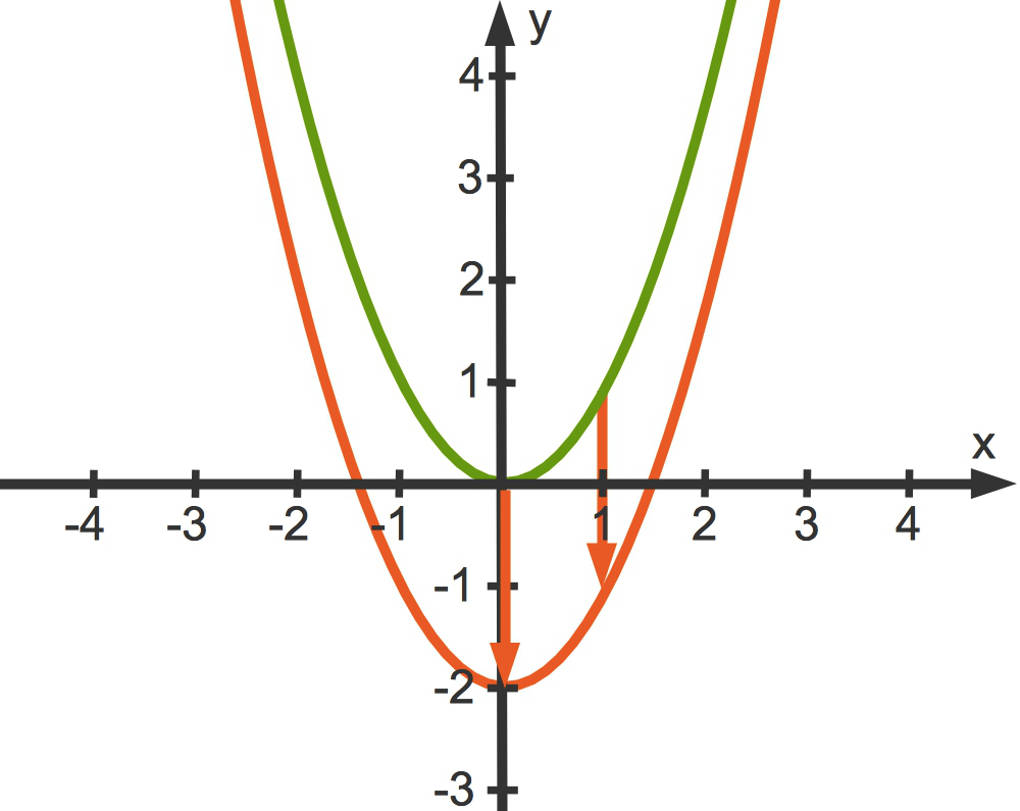
• $q(x)=x^2+1$ führt zu einer Verschiebung um $1$ Längeneinheit in positiver y-Achsen-Richtung. Der Scheitelpunkt ist $S(0|1)$.

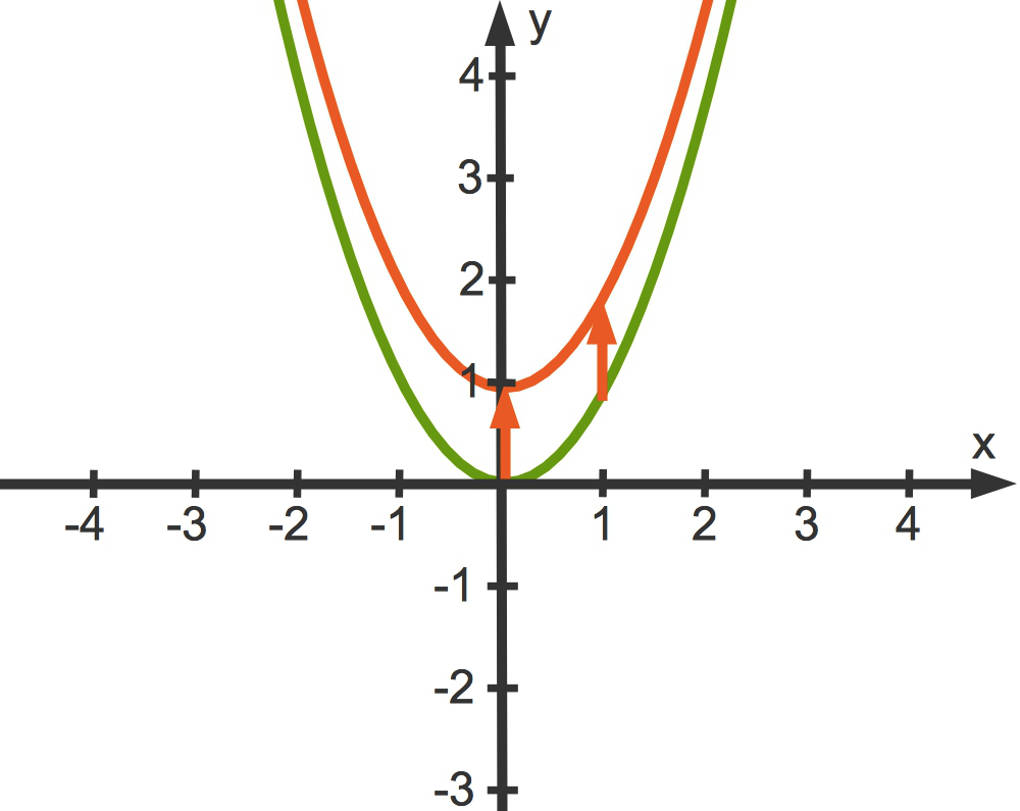
• $q(x)=x^2-2$ führt zu einer Verschiebung um $2$ Längeneinheiten in negativer y-Achsen-Richtung. Der Scheitelpunkt ist $S(0|-2)$.

Die Streckung oder Stauchung sowie Spiegelung eines Funktionsgraphen

Der Faktor $a$ ist der sogenannte Streckfaktor. Für positive $a$ gilt:

• Ist $a >1$, dann wird die Parabel in $y$-Richtung gestreckt, verläuft also enger als die Normalparabel.
• Ist $0 < a < $, dann wird die Parabel in $y$-Richtung gestaucht, verläuft also weiter als die Normalparabel.

Für negative $a$ wird die Parabel zusätzlich an der x-Achse gespiegelt.

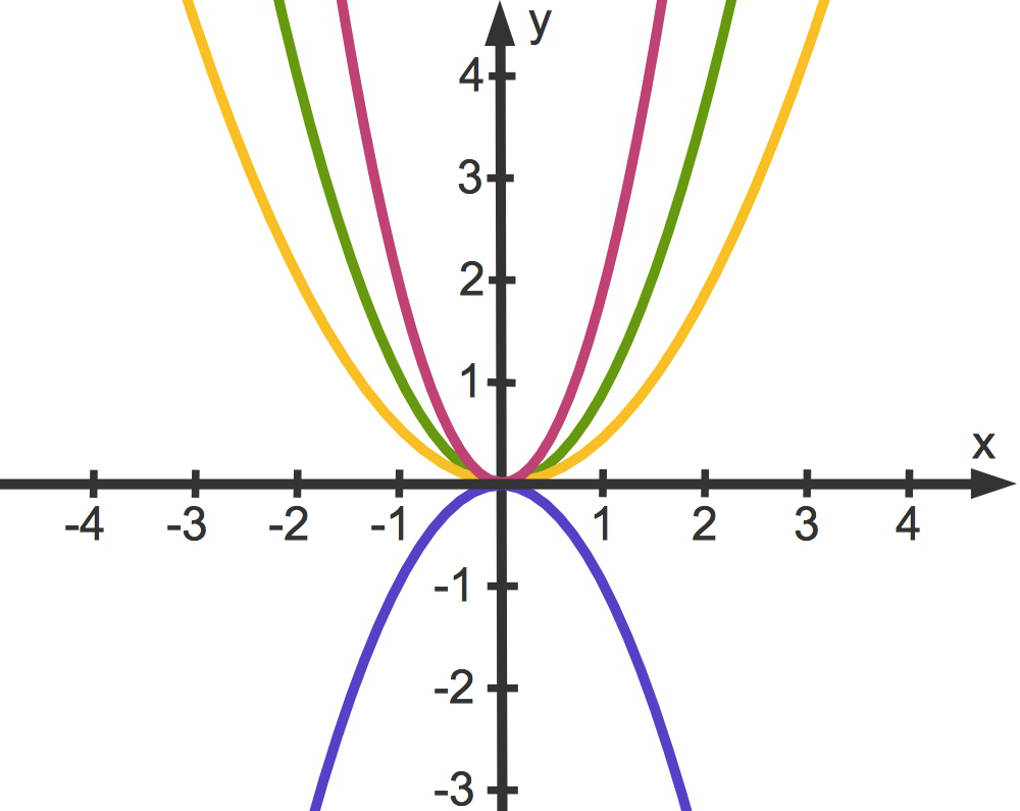
• Die rosafarbene Parabel gehört zu $q(x)=2x^2$, sie ist also gestreckt.
• Die orange Parabel gehört zu der Funktionsgleichung $q(x)=\frac12x^2$. Diese Parabel ist gestaucht.
• Die blaue Parabel ist gespiegelt. Sie gehört zu $q(x)=-x^2$.

Funktionsgraphen mit dem Parameterverfahren verschieben

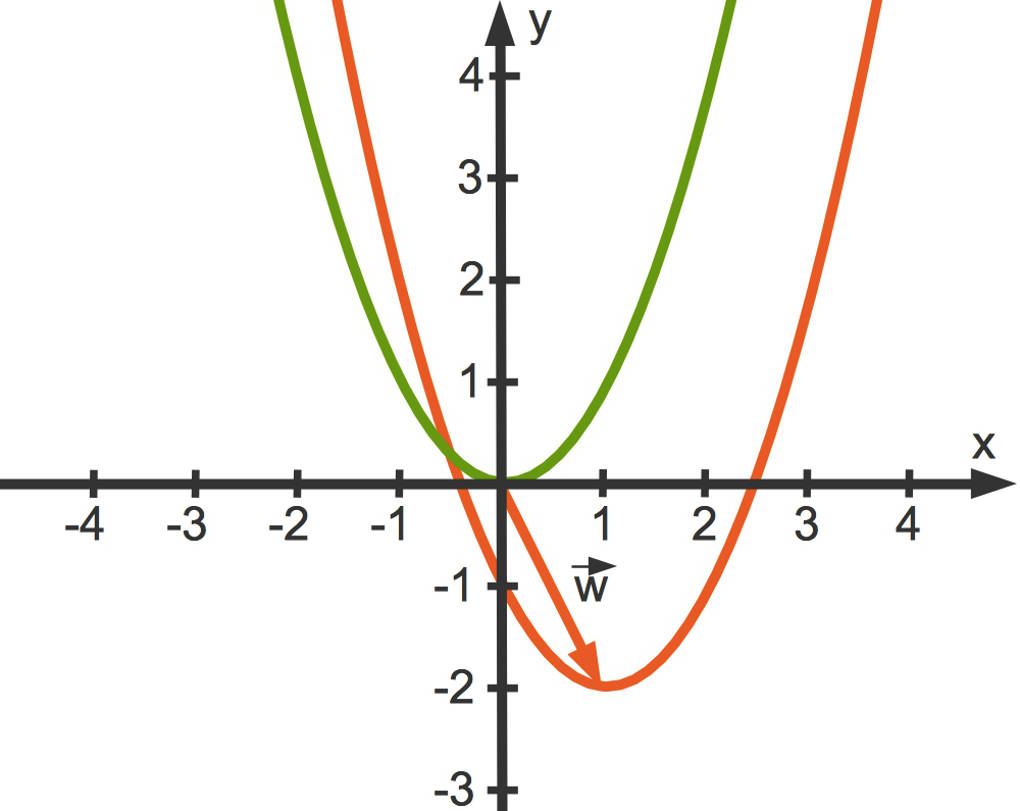
Hier siehst du, wie ein Funktionsgraph entlang eines Vektors:

$\vec w=\begin{pmatrix} 1 \\ -2 \end{pmatrix}$

verschoben wird. Die zugehörige Funktionsgleichung kannst du mit Hilfe des Parameterverfahrens herleiten. Jeder Punkt der Normalparabel $P(x|y)$ wird durch den Vektor verschoben. So entsteht ein Bildpunkt $P'(x'|y')$. Es ist

• $x'=x+1$, also $x=x'-1$, und
• $y'=y-2=x^2-2$.

Nun kann $x=x'-1$ in der Gleichung $y'=x^2-2$ eingesetzt werden. Dies führt zu:

$y'=(x'-1)^2-2=x'^2-2x'+1-2=x'^2-2x'-1$.

Zuletzt kann diese Gleichung wieder als Funktionsgleichung der verschobenen Parabel geschrieben werden: $q(x)=x^2-2x-1=(x-1)^2-2$. Der Scheitelpunkt ist $S(1|-2)$. Dieser ist der Bildpunkt des Scheitelpunktes der Normalparabel $S(0|0)$.

Die Addition von Funktionsgleichungen

Funktionsgleichungen können auch addiert werden. Grafisch wird diese Addition punktweise durchgeführt. Schauen wir uns hierfür ein Beispiel an: Es sollen die beiden Funktionen $f(x)=x^2$ sowie $g(x)=x$ addiert werden. Dies führt zu $q(x)=f(x)+g(x)=x^2+x$.

Hier siehst du entsprechenden Funktionsgraphen.

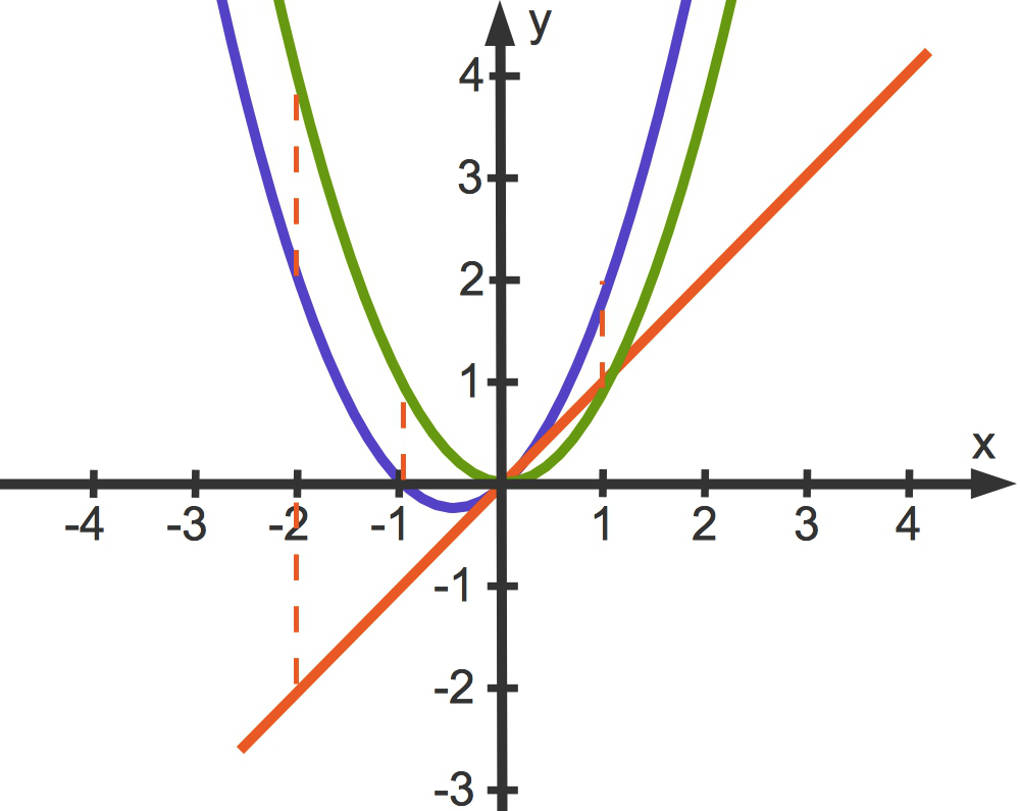
Zu dem Funktionswert $f(x)$ wird der von $g(x)$ addiert. Dies kannst du für einige $x$ an Hand der gestrichelten Linien erkennen. So entsteht aus der Addition von $f(x)$, der grünen Parabel, sowie $g(x)$, der roten Gerade, $q(x)=x^2+x$, die blaue Parabel.

Die Verknüpfung von Funktionsgleichungen

Zuletzt schauen wir uns die Verknüpfung von Funktionsgleichungen an zwei Beispielen an.

Beispiel 1

$k(x)=e^{x^2}$

Dadurch, dass im Exponenten der Exponentialfunktion die Funktion $x^2$ steht, ist der zugehörige Funktionsgraph symmetrisch zur y-Achse.

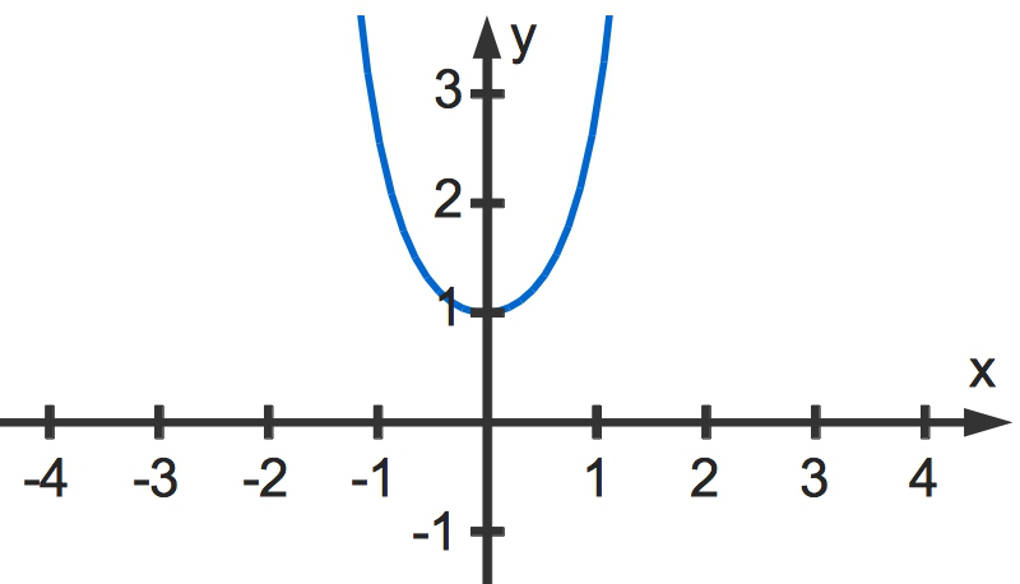
Beispiel 2

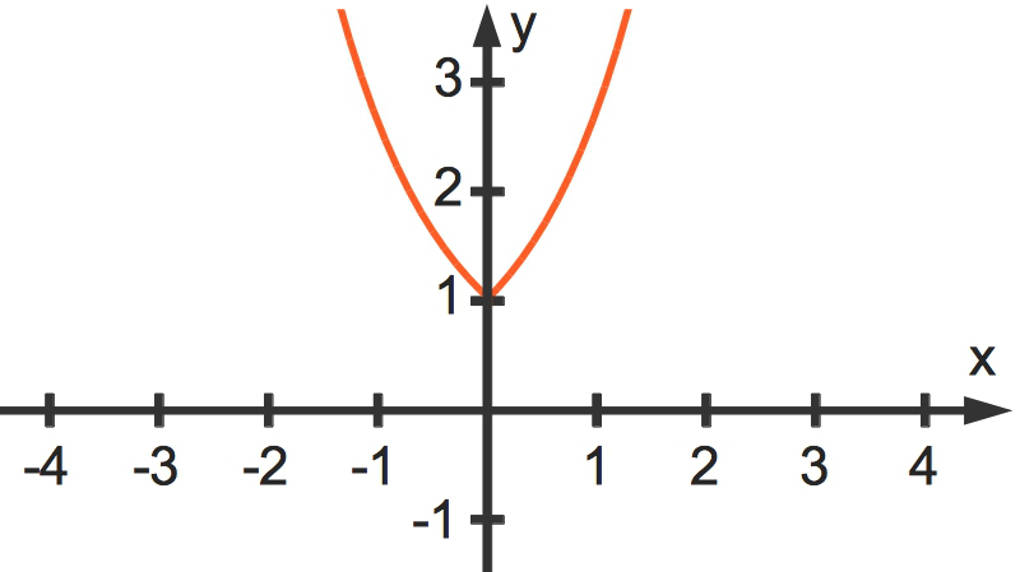
$k(x)=e^{|x|}$

Auch dieser Funktionsgraph verläuft symmetrisch zur y-Achse. Da die Betragsfunktion einen Knick hat, taucht dieser auch in dem Funktionsgraphen der verknüpften Funktion auf.