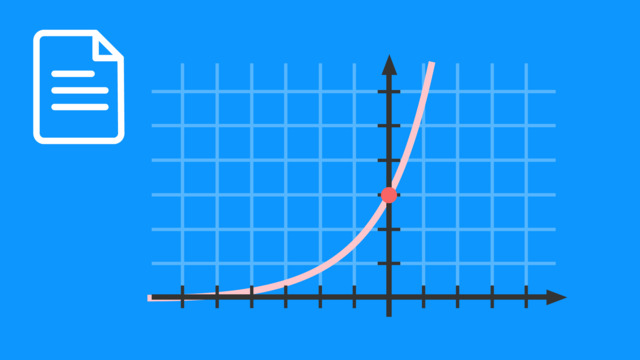
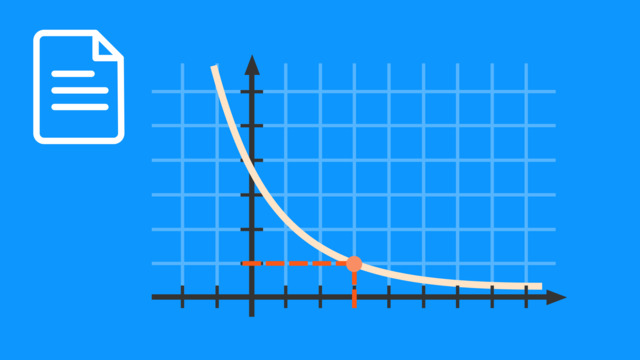
Verdopplungs- und Halbwertszeit
Die Halbwertszeit und Verdopplungszeit sind wichtige Konzepte bei Exponentialfunktionen. Sie zeigen, wie sich Größen über die Zeit verdoppeln oder halbieren. Interessiert? Erfahre mehr in den folgenden Abschnitten!
- Verdopplung und Halbierung – Einleitung
- Verdopplung und Verdopplungszeit
- Verdopplungszeit – Übung
- Berechnung der Verdopplungszeit
in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Lerntext zum Thema Verdopplungs- und Halbwertszeit
Verdopplung und Halbierung – Einleitung
Viele Prozesse im Alltag, der Industrie oder der Forschung können durch Exponentialfunktionen dargestellt werden. Man spricht dann von exponentiellem Wachstum oder auch exponentiellem Zerfall. Das sollten für dich keine unbekannten Begriffe sein. Wenn du noch etwas Auffrischung dazu brauchst, schau dir am besten zur Vorbereitung für das Thema noch einmal folgende Videos an:
- Exponentialfunktion – Definition
- Parameter der Exponentialfunktion
- Funktionsgleichung der Exponentialfunktion bestimmen
Nun wollen wir uns zwei ganz spezielle Fälle bei Exponentialfunktionen anschauen. Wir wollen nämlich den Fokus auf Verdopplung einerseits und Halbierung andererseits legen und uns anschauen, welche Besonderheiten das mit sich bringt.
Verdopplung und Verdopplungszeit
Zuerst schauen wir auf die Verdopplung von Funktionswerten bei Exponentialfunktionen bzw. auf die Verdopplungszeit. Doch was ist das eigentlich?
Die Verdopplungszeit gibt bei einer Exponentialfunktion die Zeitspanne an, nach der eine mit der Zeit zunehmende Größe das Doppelte ihres Ausgangswerts erreicht.
Ein typisches Anwendungsbeispiel aus der Biologie ist das Wachstum von Bakterien in Petrischalen. Diese betreiben nach einer bestimmten Zeit Zellteilung und verdoppeln so ihre Anzahl.
Die allgemeine Funktionsgleichung für eine Verdopplung lautet wie folgt:
$N(t)= N_0 \cdot 2^{\frac{t}{T_2}}$
$N(t)$ bezeichnet den Funktionswert (im Beispiel: die Bakterienanzahl), der von der Zeit ($t$) abhängt. $N_0$ ist der Anfangswert (also Anzahl $N$ zum Zeitpunkt „$0$“). Der Wachstumsfaktor ist in diesem speziellen Fall fest vorgegeben. Da es um die Verdopplungszeit geht, lautet die Basis der Potenz $2$. Der Exponent gibt an, wie oft die Verdopplungszeit vergangen ist. Er wird bestimmt durch die vergangene Zeit $t$ und der Verdopplungszeit des jeweiligen Funktionswerts $T_2$.
Um die Formel zu verstehen, wenden wir sie in einer Übung an.
Verdopplungszeit – Übung
In einem Labor ist eine Bakterienkultur in einer Petrischale gegeben. Sie enthält zu Beginn der Beobachtung $50$ Bakterien. Unter den günstigen Laborbedingungen verdoppelt sich die Anzahl der Bakterien alle $40$ Minuten.
Wir stellen uns folgende Fragen:
- Wie könnte man das Verhalten der Bakterien in einer Funktionsgleichung modellieren?
- Wie viele Bakterien sind nach $90$ Minuten vorhanden, wie viele nach zwei Stunden?
- Wann beträgt die Anzahl der Bakterien das $20 \text{-Fache}$ des Anfangswerts?
Für die Funktionsgleichung setzen wir einfach alle gegebenen Größen in die allgemeine Gleichung von weiter oben ein und erhalten: $N(t)= 50 \cdot 2^{\frac{t}{40}}$
Wollen wir nun den Bestand nach $90$ Minuten wissen, muss dieser Wert für $t$ eingesetzt werden: $N(90)= 50 \cdot 2^{\frac{90}{40}} \approx 50 \cdot 4{,}757 = 237{,}85 \approx 238$
Nach $90$ Minuten sind ungefähr $238$ Bakterien in der Petrischale vorhanden.
Versuche nun, für den zweiten Fall die Anzahl zu bestimmen.
Ist danach gefragt, wann ein bestimmter Wert erreicht ist (in unserem Fall das $20 \text{-Fache}$ des Anfangswerts), kann zunächst berechnet werden, nach welcher konkreten Menge gefragt ist. Dieser Wert kann dann mit der Funktionsgleichung gleichgesetzt werden, um die Zeit zu berechnen. Du wirst nachfolgend aber sehen, dass dieser Schritt auch weggelassen werden kann. Der Vollständigkeit halber soll er trotzdem einmal durchgeführt werden:
Die Anfangswert beträgt $50$ Bakterien, das $20 \text{-Fache}$ davon ist $50 \cdot 20=1 000$
Die gesuchte Zeit kann wie folgt bestimmt werden:
$\begin{array}{rcll} 1 000 & = & 50 \cdot 2^{\frac{t}{40}} & \vert :50 \\ \\ 20 & = & 2^{\frac{t}{40}} & \vert \log_{2} \\ \\ \log_{2}{20} & = & \frac{t}{40} \\ \\ 4{,}322 & \approx & \frac{t}{40} & \vert \cdot 40 \\ \\ 173 & \approx & x & \end{array}$
Es dauert also ungefähr $173$ Minuten, bis das $20$-Fache des Ausgangswerts erreicht ist.
Wie schon angekündigt siehst du in der zweiten Zeile der obigen Rechnung, dass es gar nicht zwingend notwendig ist, zunächst die gesuchte Bakterienanzahl zu berechnen. Man kann das Ganze auch vereinfacht darstellen:
$20 = 2^{\frac{t}{40}}$
Diese Gleichung kann dann nach dem obigen Schema gelöst werden. Die folgende Rechnung soll dir noch einmal verdeutlichen, warum man dies gleich so aufschreiben kann. Wir setzen dazu die Zwischenrechnung nach der gefragten Bakterienanzahl in die Gleichung ein und erhalten:
$50 \cdot 20= 50 \cdot 2^{\frac{t}{40}}$
Hier ist nun erkenntlich, dass die $50$ auf beiden Seiten der Gleichung durch Division wegfällt. Daher kannst du dir diesen Zwischenschritt des Ausrechnens sparen und die Rechnung etwas abkürzen. Das Gleiche gilt übrigens auch später bei der Halbwertszeit.
Die Verdopplungs- und die Halbwertszeit sind unabhängig vom jeweiligen Anfangsbestand.
Berechnung der Verdopplungszeit
Weiterhin kann dir auch der Fall begegnen, dass du die Verdopplungszeit nicht gegeben hast, sondern diese für eine beliebige Exponentialfunktion berechnen sollst.
Dafür ist zunächst die allgmeine Funktionsgleichung $N(t) = N_0 \cdot a^{t}$ gegeben.
Man startet mit folgender Überlegung: Verdopplungszeit bedeutet, dass sich der Anfangswert nach einer gewissen Zeit $T_2$ verdoppelt haben soll: $N(T_2)=2 \cdot N_0$
Für $N(T_2)$ setzt man dann den Funktionsterm ein und löst nach $T_2$ auf.
$N_0 \cdot a^{T_2}=2 \cdot N_0$
Zuerst kann man auf beiden Seiten durch den Anfangswert $N_0$ teilen und erhält:
$a^{T_2}=2$
Man wendet nun auf beiden Seiten den Logarithmus an. Dabei wird meist der natürliche Logarithmus verwendet.
$\ln (a^{T_2})= \ln (2)$
Die Anwendung der Logarithmusregeln ergibt:
$T_2 \cdot \ln (a) = \ln (2)$
Nach $T_2$ aufgelöst ergibt sich:
$T_2= \dfrac{\ln(2)}{\ln(a)}$
Die Verdopplungszeit lässt sich für jede beliebige Exponentialfunktion der Form $N(t) = N_0 \cdot a^{t}$ berechnen mit:
$T_2= \dfrac{\ln(2)}{\ln(a)}$
Versuche nun einmal, bei folgendem Beispiel selbstständig die Verdopplungszeit zu berechnen.
Halbwertszeit
Nachdem du die Verdopplungszeit kennengelernt hast, soll nun eine Übung zur Halbwertszeit folgen.
Die Halbwertszeit gibt bei einer Exponentialfunktion die Zeitspanne an, nach der eine mit der Zeit abnehmende Größe die Hälfte ihres Anfangswerts erreicht.
Auch für die Funktionsgleichung zur Halbwertszeit gibt es eine spezielle Formel:
$N(t)= N_0 \cdot \left(\dfrac{1}{2}\right)^{\dfrac{t}{T_\frac{1}{2}}}$
$N(t)$ bezeichnet die gesuchte Menge der Radionuklide, die von der Zeit ($t$) abhängen. $N_0$ ist der Anfangswert (also Anzahl $N$ zum Zeitpunkt „$0$“). Der Wachstumsfaktor sieht hier etwas anders aus. Da es um die Halbwertszeit geht, lautet die Basis $\frac{1}{2}$. Der Exponent gibt an, wie oft die Halbwertszeit vergangen ist. Er wird bestimmt durch die vergangene Zeit $t$ und die Halbwertszeit des jeweiligen Elements $T_\frac{1}{2}$.
Halbwertszeit – Übung
Anhand folgender Aufgabe wollen wir dies nun einmal üben:
Bei dem bekannten Reaktorunglück in Fukushima wurden verschiedene radioaktive Substanzen freigesetzt. Besonders relevant für die radioaktive Kontamination der Umwelt (und des Menschen) nach dem Unfall waren Radionuklide der Elemente $\text{Jod-}131$ und $\text{Cäsium-}137$.
Zu Beobachtungsbeginn liegen $145 ~\text{mg} ~\text{Jod-}131$ sowie $350 ~\text{mg} ~\text{Cäsium-}137$ vor.
Über die Halbwertszeiten der Elemente ist Folgendes bekannt:
- $\text{Jod-}131$ hat eine Halbwertszeit von etwa $8$ Tagen
- $\text{Cäsium-}137$ hat eine Halbwertszeit von ca. $30$ Jahren.
Folgende Teilaufgaben sollen bearbeitet werden:
- Welche Mengen der radioaktiven Nuklide liegen nach $25$ Tagen vor, wie viel nach $3$ Jahren?
- Wie lange dauert es, bis nur noch $10\,\%$ der ursprünglichen Mengen der Radionuklide vorliegen?
$\text{Jod-}131$
Wir beginnen mit der Berechnung für den Zerfall von $\text{Jod-}131$.
Für die Funktionsgleichung ergibt sich:
$N_{\text{Iod}}(t)= 145 \cdot \left(\frac{1}{2}\right)^{\frac{t}{8}}$ mit $t$ in Tagen
Soll nun die Menge nach $25$ Tagen bestimmt werden, muss diese Zeitspanne einfach für $t$ eingesetzt werden:
$N_{\text{Iod}} (25) = 145 \cdot \left(\frac{1}{2}\right)^{\frac{25}{8}} \approx 16{,}62 $
Nach $25$ Tagen liegen also noch $16{,}62~ \text{mg}~ \text{Jod-}131$ vor.
Wollen wir nun die Menge an Jod nach $3$ Jahren berechnen, müssen wir einen weiteren Schritt beachten. Da die Halbwertszeit von Jod in der Einheit „Tage“ angegeben ist, müssen wir auch für $t$ einen Wert in „Tagen“ einsetzen – dazu müssen die $3$ Jahre in Tage umgerechnet werden:
$3 ~\text{Jahre} = 3 \cdot 365~ \text{Tage} = 1 095~ \text{Tage}$
Anschließend kann wie gewohnt eingesetzt und berechnet werden:
$N_{\text{Iod}} (1095) =145 \cdot \left(\frac{1}{2}\right)^{\frac{1 095}{8}} \approx 9{,}08 \cdot 10^{-40}$
Nach $3$ Jahren liegt also noch $9{,}08 \cdot 10^{-40} ~\text{mg}$ vor. In der Realität bedeutet dies, dass das Jod zu diesem Zeitpunkt beinahe vollständig abgebaut ist.
Wollen wir nun wissen, zu welchem Zeitpunkt nur noch $10\,\%$ der ursprünglichen Menge vorliegen, könnte man einen Extraschritt gehen und zuerst berechnen, wie viel $10\,\%$ der ursprünglichen Menge sind und dies dann mit dem Funktionsterm gleichsetzen. Da du aber weiter oben bei der Verdopplungszeit schon gesehen hast, dass Verdopplungs- und Halbwertszeit unabhängig vom Anfangsbestand sind, kannst du dir diesen Schritt sparen.
Wir können also gleich berechnen:
$\begin{array}{rcll} 0{,}1 & = & \left(\frac{1}{2}\right)^{\frac{t}{8}} & \vert \log_{\left(\frac{1}{2}\right)} \\ \\ \log_{\left(\frac{1}{2}\right)}{0{,}1} & =& \frac{t}{8} & \, \\ \\ \frac{t}{8}& \approx & 3{,}322& &\vert \cdot 8 \\ \\ t & \approx & 27 & \, \end{array}$
Nach ca. $27$ Tagen sind also nur noch $10\,\%$ des ursprünglichen Jods vorhanden.
Versuche nun, die Aufgaben für das andere Radionuklid selbst zu lösen.
$\text{Cäsium-}137$
Berechnung der Halbwertszeit
Es kann dir (wie oben bei der Verdopplungszeit) allerdings auch der Fall begegnen, dass du für einen gegebenen exponentiellen Zerfall die Halbwertszeit nicht gegeben hast, sondern berechnen sollst.
Es gilt analog zur Herleitung der Verdopplungszeit:
Die Halbwertszeit lässt sich für jede beliebige Exponentialfunktion der Form $N(t) = N_0 \cdot a^{t}$ berechnen mit:
$T_\frac{1}{2}= \frac{\ln \left(\frac{1}{2}\right)}{\ln(a)}$
Exkurs – die Radiokarbonmethode
Eine ganz spezielle Anwendung der Halbwertszeit lässt sich in der Radiokarbonmethode (oder auch $^{14}\text{C}$-Methode) finden. Diese wird zur Altersbestimmung kohlenstoffhaltiger Materialien verwendet. Dabei wird der Fortschritt des Zerfalls des Kohlenstoffisotops $^{14}\text{C}$ gemessen und analysiert. Das $^{14}\text{C}$-Kohlenstoffisotop besitzt eine Halbwertszeit von $5 730$ Jahren. Das bedeutet, dass sich in dieser Zeit die Menge an $^{14}\text{C}$ im Organismus halbiert, während der Anteil an klassischem, stabilem Kohlenstoff bestehen bleibt.
Da der Anteil am klassischen Kohlenstoff immer gleich bleibt und das instabile Kohlenstoffisotop zerfällt, kann man durch das heutige Verhältnis der Mischung beider Kohlenstoffe auf das Alter der Probe schließen.
Da das gesamte Prinzip der Radiokarbonmethode auf dem Zerfallsgesetz basiert, ist dieses auch die Grundlage für die rechnerische Lösung des Alters. Die Funktionsgleichung lautet wie folgt:
$N(t)=N_0 \cdot e^{-\lambda \cdot t}$
Dabei gibt $N(t)$ die Anzahl der noch heute vorhandenen Atomkerne an, $N_0$ die Anzahl der am Anfang vorhandenen Atomkerne, $t$ die vergangene Zeit und das $\lambda$ ist die Zerfallskonstante. Diese berechnet sich durch:
$\lambda = \dfrac{\ln(2)}{T_\frac{1}{2}}$
Dabei bezeichnet $T_\frac{1}{2}$ die Halbwertszeit. Setzt man nun die Zerfallskonstante $\lambda$ in das Zerfallsgesetz ein, ergibt sich:
$N(t)=N_0 \cdot e^{-\dfrac{\ln(2)}{T_\frac{1}{2}} \cdot t}$
Häufig werden dir Aufgaben begegnen, in denen du das Alter einer Probe (also die vergangene Zeit) anhand einer gemessenen Anzahl an Atomkernen und einer Referenz als Ausgangswert bestimmen sollst. Stellt man die Gleichung nach $t$ um (also nach der vergangenen Zeit), ergibt sich für $t$:
$t=\dfrac{\ln (\frac{N(t)}{N_0}) \cdot T_\frac{1}{2}}{- \ln(2)}$
Dabei ist $t$ das Alter, $N_0$ ist die Anzahl der $^{14}\text{C}$-Atome vor dem Zerfall (meist durch eine Vergleichsprobe), $N(t)$ ist die Anzahl der gemessenen Atome bei der Messung und $T_\frac{1}{2}$ bezeichnet die Halbwertszeit.
Anhand des folgenden Beispiels wollen wir dies nun einmal anwenden.
Bei einer Probe wird die Anzahl von $N(t)= 1{,}2 \cdot 10^{5}$ an $^{14}\text{C}$-Atomen gemessen. Bei der Referenzprobe wird eine Anzahl von $N(t)= 3{,}6 \cdot 10^{5}$ bestimmt. Diese Anzahl entspricht also dem Anfangswert. Es ist bekannt, dass die Halbwertszeit $5 730$ Jahre beträgt. Wie alt ist die entnommene Probe?
Aus der oben beschriebenen Formel kann durch Einsetzen das Alter der Probe bestimmt werden:
$\begin{array}{rcl} t&=& \dfrac {\ln (\frac{1{,}2 \cdot 10^{5}}{3{,}6 \cdot 10^{5}}) \cdot 5 730}{- \ln(2)} \\ \\ t&=& \dfrac {\ln (\frac{1}{3}) \cdot 5 730}{- \ln(2)} \\ \\ t& \approx & \dfrac{- 6\,295{,}048}{- \ln(2)} \\ \\ t& \approx & 9\,082 [\text{a}] \end{array}$
Die Probe ist also ungefähr $9\,082$ Jahre alt.
Verdopplungs- und Halbwertszeit – Zusammenfassung
Die allgemeine Funktionsgleichung für eine Verdopplung lautet wie folgt:
$N(t)= N_0 \cdot 2^{\frac{t}{T_2}}$
Halbiert sich eine Größe, kann die allgemeine Funktionsgleichung angegeben werden mit:
$N(t)= N_0 \cdot \left(\frac{1}{2}\right)^{\frac{t}{T_\frac{1}{2}}}$
Die Verdopplungs- und die Halbwertszeit sind unabhängig vom jeweiligen Anfangsbestand. Sie können für jede beliebige Exponentialfunktion der Form $N(t) = N_0 \cdot a^{t}$ berechnet werden mit:
- Verdopplungszeit: $T_2= \frac{\ln(2)}{\ln(a)}$
- Halbwertszeit: $T_\frac{1}{2}= \frac{\ln \left(\frac{1}{2}\right)}{\ln(a)}$
9.711
sofaheld-Level
6.600
vorgefertigte
Vokabeln
7.787
Lernvideos
37.112
Übungen
32.540
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Schulstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung


 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?