Dreiecke – Arten, Umfang und Flächeninhalt
Das Dreieck ist eines der Grundelemente in der Geometrie. Wie man den Umfang und die Fläche eines Dreiecks berechnet, lernst du hier.
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
Was ist ein Dreieck?
Ein Dreieck ist eine ebene Figur.
Ein Dreieck hat, wie du an dem Namen bereits erkennen kannst, drei Ecken. Ein Dreieck hat auch drei Seiten und drei Winkel.
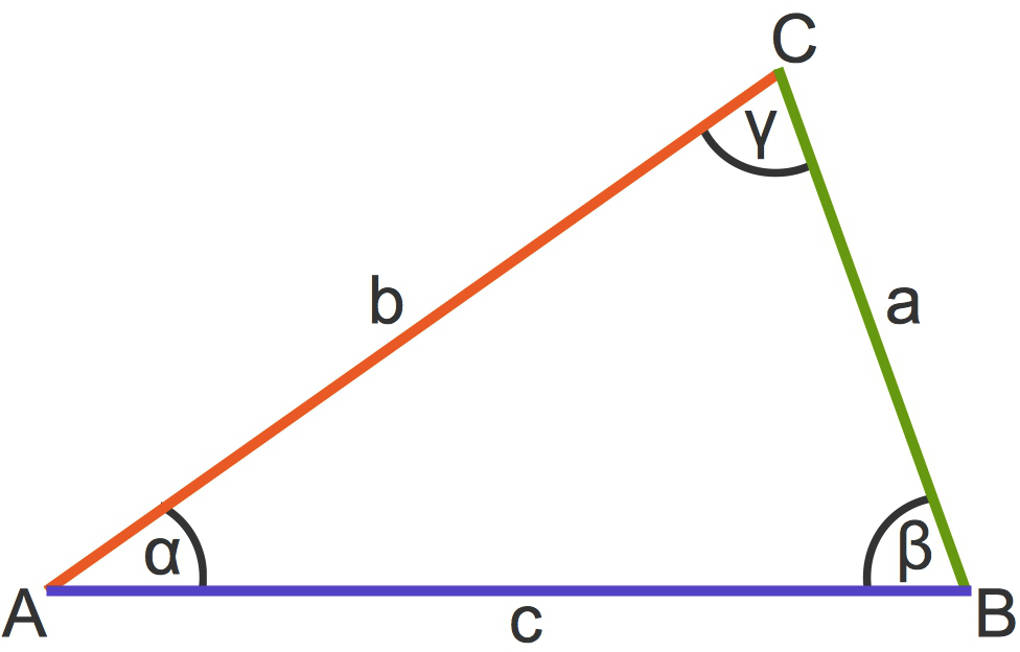
Du kannst hier ein allgemeines Dreieck sehen mit den entsprechenden Bezeichnungen der Ecken, Seiten und Winkel.
Der Umfang eines Dreiecks
Den Umfang eines Dreiecks kannst du dir wie folgt klarmachen: Du startest bei dem Punkt $A$ und gehst zu $B$, die Länge der Strecke ist $c$. Von dort gehst du zu $C$. Gesamt bist du bereits $c+a$ gegangen. Zurück zu $A$ gehst du die Strecke $b$. Der gesamte Weg ist der Umfang:
$\quad~~~U=a+b+c$.
Beispiel
In einem See sind für ein Schwimmwettbewerb die Bahnen in Form eines Dreiecks abgesteckt. Die eine Seite ist $300~m$ lang, eine weitere $500~m$ und die letzte $400~m$. Die Teilnehmer des Schwimmwettbewerbes müssen zwei Runden schwimmen. Wie lang ist die gesamte Schwimmstrecke?
- Zuerst muss der Umfang des Dreiecks berechnet werden:
$\quad~~~U=300~m+500~+400~=1200~m$.
- Dieser wird mit $2$ multipliziert: $2\cdot 1200~m=2400~m$. Dies ist die gesamte Länge der Schwimmstrecke.
Die Fläche eines Dreiecks
Rechtwinklige Dreiecke
Ein rechtwinkliges Dreieck ist ein Dreieck mit einem rechten Winkel. Die Seite, die dem rechten Winkel gegenüberliegt, wird als Hypotenuse bezeichnet und die beiden anderen Seiten als Katheten.
Hier siehst du ein Rechteck.
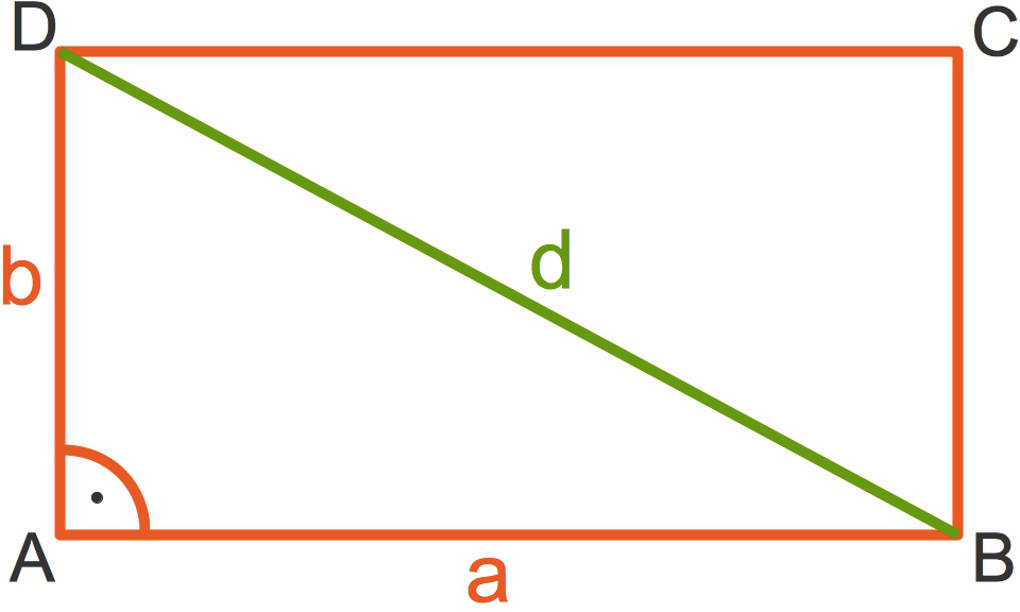
Die grüne Diagonale teilt dieses Rechteck in zwei deckungsgleiche (kongruente) rechtwinklige Dreiecke. Das bedeutet, dass diese Dreiecke den gleichen Flächeninhalt haben. Somit ist
$\quad~~~2\cdot A_{\Delta}=A_{\text{Rechteck}}=a\cdot b$.
Division durch $2$ führt zu dem Flächeninhalt von rechtwinkligen Dreiecken
$\quad~~~A_{\Delta}=\frac{a\cdot b}2$
Dabei sind $a$ und $b$ die Katheten des Dreiecks.
Allgemeine Dreiecke
Um den Flächeninhalt eines beliebigen Dreiecks zu berechnen, kannst du Hilfslinien in dem obigen Dreieck einfügen:
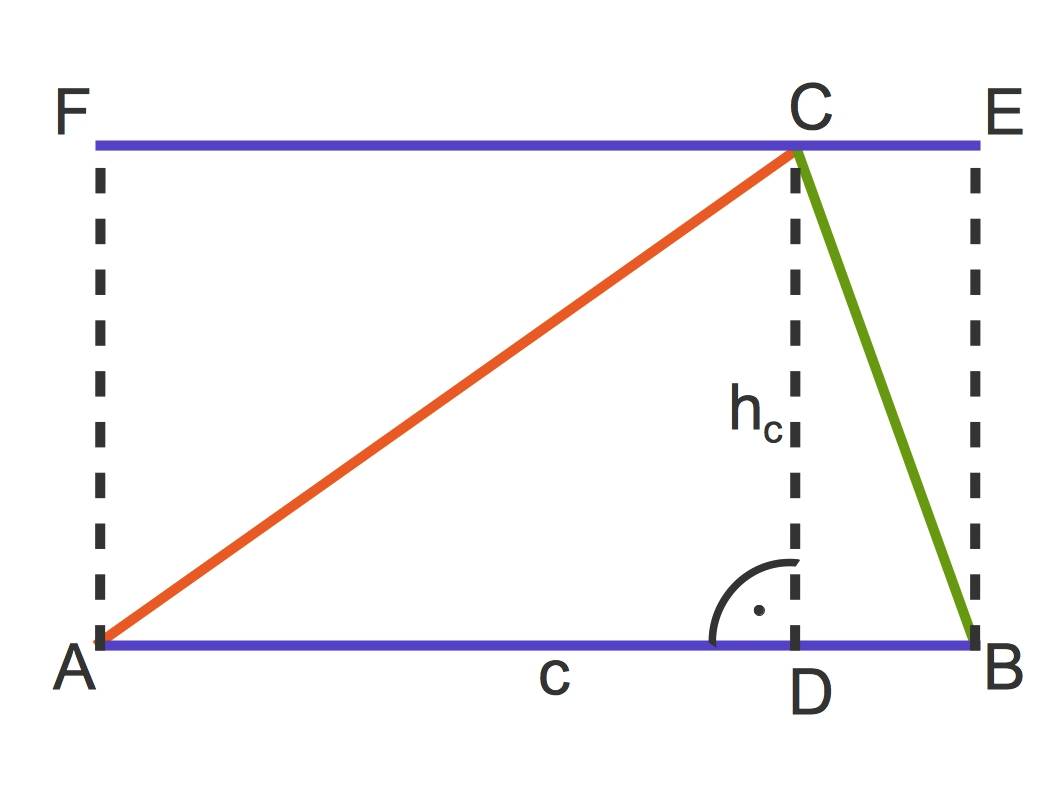
- $c$ ist die Grundseite und
- $h_c$ ist die Höhe des Dreiecks. Diese erhältst du, indem du von dem Punkt $C$ aus auf die gegenüberliegende Seite $c$ das Lot fällst.
Das gesamte Rechteck mit den Ecken $A$, $B$, $E$ und $F$ hat den Flächeninhalt
$\quad~~~A_{\text{Rechteck}}=c\cdot h_c$.
.
Die beiden Dreiecke $\Delta_{ADC}~$ und $\Delta_{ACF}~$ sind kongruent, haben also den gleichen Flächeninhalt. Das gilt auch für die Dreiecke $\Delta_{DBC}~$ und $\Delta_{BEC}$.
Da der Flächeninhalt des Dreiecks $\Delta_{ABC}~$ genau die Summe der Flächeninhalte der Dreiecke $\Delta_{ADC}~$ und $\Delta_{DBC}~$ ist, gilt:
$\quad~~~A=\frac{c~\cdot~ h_c}2$.
Ein Dreieck hat drei Höhen $h_a$, $h_b$ und $h_c$. Jede dieser Höhen erhältst du ebenso wie oben beschrieben.
Hier siehst du das Dreieck mit der Höhe $h_c$.
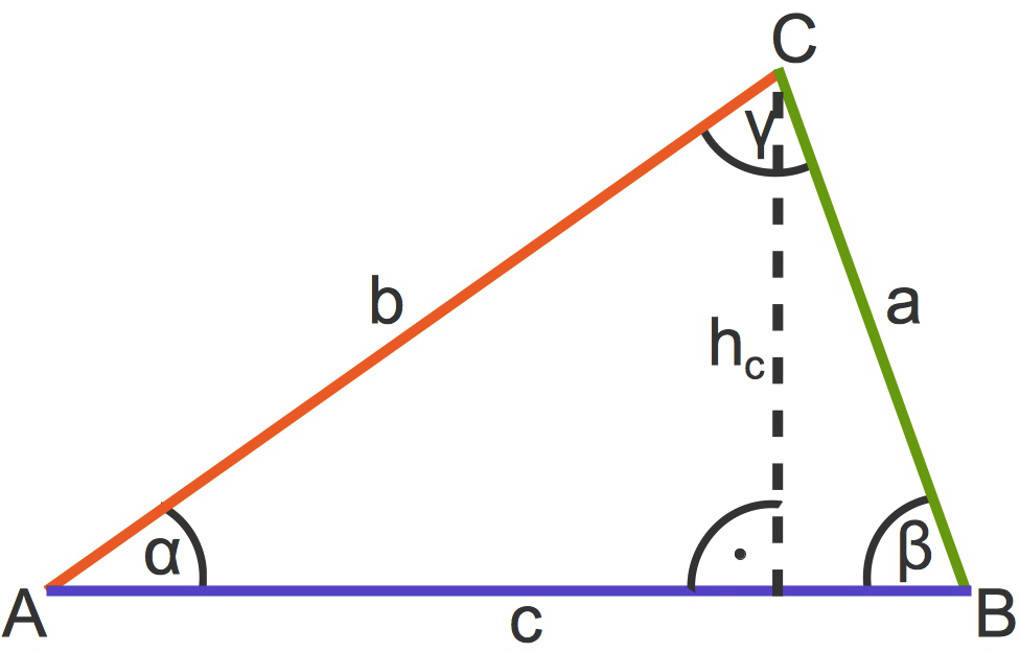
Somit ist die Fläche eines beliebigen Dreiecks gegeben durch die Formel(n)
$\quad~~~A=\frac{c~\cdot~ h_c}2=\frac{a~\cdot~ h_a}2=\frac{b~\cdot~ h_b}2$.
Diese Formel ist natürlich auch anwendbar auf rechtwinklige Dreiecke: Zwei der drei Höhen eines rechtwinkligen Dreiecks sind die Katheten.
Exkurs: Seitenlängen berechnen
Paul möchte in seinem Zimmer ein rechtwinkliges Dreieck an die Wand malen. Die Hypotenuse $c$ ist $5~m$ lang und eine der Katheten (parallel zum Boden), $a$, genau $4~m$ lang. Die Menge der Farbe hängt von der Fläche ab. Wie groß ist die Fläche dieses Dreiecks?
In einem rechtwinkligen Dreieck ist der Flächeninhalt die Hälfte des Produktes der beiden Katheten.
Paul muss zuerst die fehlende Kathetenlänge $b$ berechnen. Hierfür verwendet er den Satz des Pythagoras. Es gilt
$\quad~~~b^2+(4~m)^2=(5~m)^2$.
Jetzt wird auf beiden Seiten $(4~m)^2$ subtrahiert zu $b^2=25~m^2-16~m^2=9~m^2$. Ziehen der Wurzel führt zu $b=3~m$. Paul kennt somit beide Kathetenlängen und kann den Flächeninhalt berechnen:
$\quad~~~A=\frac{(4~m)\cdot (3~m)}{2}=\frac{12~m^2}{2}=6~m^2$.
Paul muss also Farbe für $6~m^2$ besorgen.
Alle Videos und Lerntexte zum Thema
Videos und Lerntexte zum Thema
Dreiecke – Arten, Umfang und Flächeninhalt (12 Videos, 1 Lerntext)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Dreiecke – Arten, Umfang und Flächeninhalt (12 Arbeitsblätter)
-
 Aufbau von Dreiecken
PDF anzeigen
Aufbau von Dreiecken
PDF anzeigen -
 Dreiecksarten
PDF anzeigen
Dreiecksarten
PDF anzeigen -
 Umfang von Dreiecken
PDF anzeigen
Umfang von Dreiecken
PDF anzeigen -
 Flächeninhalt von Dreiecken berechnen
PDF anzeigen
Flächeninhalt von Dreiecken berechnen
PDF anzeigen -
 Flächeninhalt von rechtwinkligen Dreiecken
PDF anzeigen
Flächeninhalt von rechtwinkligen Dreiecken
PDF anzeigen -
 Seiten und Winkel im Dreieck
PDF anzeigen
Seiten und Winkel im Dreieck
PDF anzeigen -
 Innenwinkelsummen von Dreiecken
PDF anzeigen
Innenwinkelsummen von Dreiecken
PDF anzeigen -
 Innenwinkel und Außenwinkel von Dreiecken
PDF anzeigen
Innenwinkel und Außenwinkel von Dreiecken
PDF anzeigen -
 Basiswinkelsatz – Erklärung und Umkehrung
PDF anzeigen
Basiswinkelsatz – Erklärung und Umkehrung
PDF anzeigen -
 Fehlende Größen im Dreieck berechnen
PDF anzeigen
Fehlende Größen im Dreieck berechnen
PDF anzeigen -
 Dreiecksungleichung – Erklärung
PDF anzeigen
Dreiecksungleichung – Erklärung
PDF anzeigen -
 Dreiecke aus gegebenen Angaben zeichnen
PDF anzeigen
Dreiecke aus gegebenen Angaben zeichnen
PDF anzeigen
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
























