Wurzelfunktionen – Kurvendiskussion
Definitionsbereich, Wertebereich, Nullstellen, Symmetrie, Extrema, Wendepunkte, Verhalten im Unendlichen, Schnittpunkt y-Achse, Sattelpunkte, Graph
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
Kurvendiskussion einer Wurzelfunktion
Im Folgenden wird die Kurvendiskussion einer Wurzelfunktion betrachtet. Dabei untersuchen wir die Funktion auf folgende Eigenschaften:
- Definitionsbereich
- Symmetrie
- Ableitungen
- Achsenschnittpunkte
- Extrema
- Wendepunkte
Anschließend fertigen wir anhand der ermittelten Eigenschaften eine Skizze des zugehörigen Funktionsgraphen an. Wir betrachten nun beispielhaft folgende Wurzelfunktion:
$f(x) = \sqrt{x} -x$
Definitionsbereich
Der Ausdruck unter einer Wurzel darf größer gleich Null sein. Demnach darf man für $x$ alle positiven reellen Zahlen und die Null einsetzen. Die Funktion $f$ besitzt also folgenden Definitionsbereich:
$D_f = \mathbb{R}^{+}_0$
Symmetrie
Zunächst untersuchen wir die Funktion auf Achsensymmetrie zur $y$-Achse. Hierzu muss $f(x)=f(-x)$ gelten. Wir setzen also in die Funktion $-x$ ein und überprüfen, ob die Bedingung erfüllt ist:
$f(-x)=\sqrt{-x}-(-x)=\sqrt{-x}+x\neq f(x)$
Demnach ist die betrachtete Wurzelfunktion nicht symmetrisch zur $y$-Achse. Sie ist auch nicht punktsymmetrisch zum Koordinatenursprung, da $f(x) \neq -f(-x)$ gilt.
Ableitungen
Die Ableitung einer Wurzelfunktion lässt sich leichter ermitteln, wenn man mit der Potenzschreibweise arbeitet. Für das Ableiten betrachten wir also folgende Funktion:
$f(x) = x^{\frac{1}{2}} - x$
Die erste Ableitung können wir nun nach den bekannten Regeln bilden:
$\begin{array}{lll} f'(x) &=& \frac{1}{2}x^{\frac{-1}{2}} - 1\\ &=& \frac{1}{2\sqrt{x}} - 1 \end{array}$
Die zweite Ableitung erhalten wir auf dieselbe Weise:
$\begin{array}{lll} f''(x) &=& -\frac{1}{4}\cdot x^\frac{-3}{2} \\ &=& -\frac{1}{4\sqrt{x^{3}}} \end{array}$
Wir können hier erkennen, dass die zweite Ableitung nicht $0$ werden kann. Somit ist schon mal ausgeschlossen, dass es einen Wendepunkt gibt. Eine dritte Ableitung wird also nicht gebraucht.
Nullstellen
Wir ermitteln die Nullstellen, indem wir die Funktionsgleichung mit $0$ gleichsetzen. Doch warum erhalten wir auf diese Weise die Nullstellen?
Die Nullstellen sind die $x$-Werte, bei denen der Funktionsgraph die $x$-Achse schneidet. In einem Schnittpunkt mit der $x$-Achse ist der zugehörige Funktionswert (also $y$-Wert) immer gleich $0$. Somit folgt für $f(x)=0$ folgende Gleichung:
$\begin{array}{lll} 0 &=&\sqrt{x} -x \\ 0 &=& \sqrt{x}\cdot \left(1-\sqrt{x}\right) \end{array}$
Laut dem Satz vom Nullprodukt ist ein Produkt genau dann $0$, wenn einer der Faktoren $0$ ist. Daraus folgt für den ersten Faktor:
$\begin{array}{lll} \sqrt{x} &=& 0 \\ x_1 &=& 0 \end{array}$
Mit dem zweiten Faktor erhalten wir:
$\begin{array}{llll} 1-\sqrt{x} &=& 0 & \vert +\sqrt{x} \\ 1 &=& \sqrt{x} & \\ 1 &=& x_2 & \\ \end{array}$
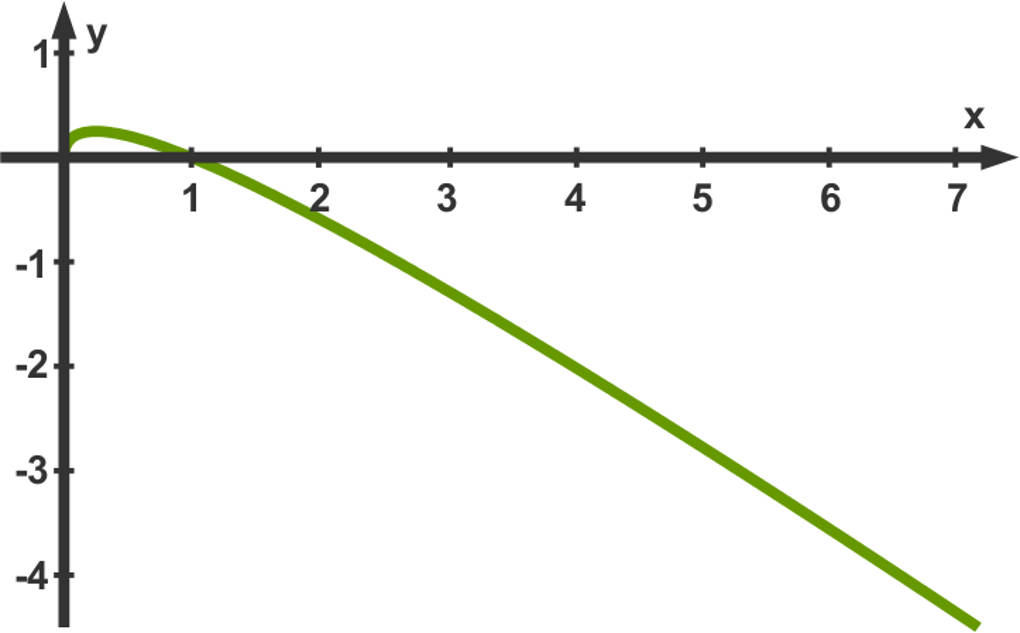
Wir erhalten also die beiden Nullstellen $N_{1} (0|0)$ und $N_{2} (1|0)$.
Extrema
Unter den Extrema verstehen wir die Hoch- und Tiefpunkte der Funktion. Diese können wir durch notwendige und hinreichende Kriterien bestimmen.
notwendiges Kriterium: $f'(x) = 0$
Sehen wir die erste Ableitung als Steigung der Tangente in einem Punkt der Funktion, so hat sie in den Extremstellen eine Steigung von $0$ und verläuft somit parallel zur $x$-Achse.
$\frac{1}{2}\cdot \frac{1}{\sqrt{x}} - 1 = 0$
Durch Umformen erhalten wir:
$\begin{array}{llll} 2\cdot\sqrt{x} &=& 1 & \vert :2\\ \sqrt{x} &=& \frac{1}{2} & \\ x &=& \frac{1}{4} & \end{array}$
hinreichendes Kriterium: $f''(x)\neq{0}$
$f''(\frac{1}{4}) = -\frac{1}{4}\cdot \frac{1}{\sqrt{(\frac{1}{4})^{3}}} = -2$
Da $-2\lt0$, handelt es sich um einen Hochpunkt mit der $x$-Koordinate $\frac{1}{4}$.
Die $y$-Koordinate errechnen wir durch Einsetzen des $x$-Wertes in die Ausgangsfunktion:
$f(\frac{1}{4})=\sqrt{\frac{1}{4}} - \frac{1}{4} = \frac{1}{4}$
Die Funktion $f$ besitzt somit einen Hochpunkt bei $\text{H}_\text{P}(\frac{1}{4}|\frac{1}{4})$.
Wendepunkte
Ein Wendepunkt ist die Stelle eines Graphen, in dem er sein Krümmungsverhalten ändert. Die notwendige Bedingung für die Existenz eines Wendepunktes ist $f''(x)=0$. Da die zweite Ableitung der hier betrachteten Wurzelfunktion stets ungleich Null ist, ist die Existenz eines Wendepunktes ausgeschlossen.
Skizze
Wir tragen die ermittelten markanten Punkte (Nullstellen und Hochpunkt) in das Koordinatensystem ein und beachten den Grenzwert für $x\rightarrow\infty$.
Winkelfunktionen
Was ist eine Winkelfunktion. Eine Winkelfunktion oder auch trigonometrische Funktion ist eine Funktion, in welcher der Sinus, der Cosinus oder der Tangens vorkommen.
Hier siehst du Beispiele für Winkelfunktionen:
- $f(x)=\sin(x)$
- $g(x)=(\cos(x))^2$
- $h(x)=\sin(x+1)-3$
Diese Liste kann natürlich beliebig erweitert werden.
Häufig wirst du Aufgaben bearbeiten müssen, welche Teile einer Kurvendiskussion sind oder aber eine komplette Kurvendiskussion.
Die einzelnen Punkte einer Kurvendiskussion sollten dir dabei bekannt sein.
Die Ableitungen der trigonometrischen Funktionen
Wie funktioniert die Kurvendiskussion bei trigonomischen Funktionen? Für die Ableitungen der trigonometrischen Funktionen Sinus und Cosinus kannst du dir die folgende Listung merken. Dabei ist immer eine Funktion gegeben und die darunter stehende ist deren Ableitung. Übrigens: Wenn du die Liste von unten nach oben betrachtest, erhältst du auch gleich eine jeweilige Stammfunktion.
- $\sin(x)$
- $\cos(x)$
- $-\sin(x)$
- $-\cos(x)$
- $\sin(x)$ ... jetzt bist du wieder an dem Ausgangspunkt.
Wir schauen uns nun an einem Beispiel eine solche Kurvendiskussion an.
Beispiel $f(x)=(\cos(x))^2$
Wir beginnen mit dem Definitionsbereich:
Da die Cosinusfunktion für alle $x\in\mathbb{R}$ definiert ist, gilt dies auch für $f(x)$. Somit ist $\mathbb{D}_{f}=\mathbb{R}$.
Kommen wir zum Wertebereich. Hierfür schauen wir uns einmal den Wertebereich von Cosinus an, dieser ist das abgeschlossene Intervall $[-1;1]$. Durch das Quadrieren erhältst du den folgenden Wertebereich für die Funktion $f$. Dieser ist $\mathbb{W}_{f}=[0,1]$.
Nullstellen
Zur Untersuchung einer Funktion $f$ auf Nullstellen löst du die Gleichung $f(x)=0$.
Los geht's:
- $(\cos(x))^2=0$: Zunächst ziehst du die Wurzel und erhältst damit
- $\cos(x)=0$: Die Nullstellen der Cosinusfunktion sind gegeben durch $\frac{\pi}2+k\cdot \pi$, wobei $k\in\mathbb{Z}$ gilt.
Symmetrie
Du prüfst, ob einer der beiden Fälle gilt:
- $f(-x)=f(x)$: Die Funktion ist achsensymmetrisch zur $y$-Achse.
- $f(-x)=-f(x)$: Die Funktion ist punktsymmetrisch zum Koordinatenursprung.
- Andernfalls liegt keine der beiden obigen Symmetrien vor.
Du ersetzt also in der Funktionsgleichung $x$ durch $-x$ und erhältst $f(-x)=(\cos(-x))^2$. Da der Cosinus achsensymmetrisch zur $y$-Achse ist, gilt $\cos(-x)=\cos(x)$ und somit $f(-x)=(\cos(-x))^2=(\cos(x))^2=f(x)$. Die Funktion $f$ ist somit ebenfalls achsensymmetrisch zur $y$-Achse.
Extrema
Für die Untersuchung auf Extrema benötigst du die ersten beiden Ableitungen:
- $f(x)=(\cos(x))^2$
- Hier verwendest du die Kettenregel sowie die Ableitung von Cosinus: $f'(x)=2\cdot \cos(x)\cdot (-\sin(x))=-2\cdot \cos(x)\cdot \sin(x)$.
- Mit der Produktregel erhältst du die zweite Ableitung: $f''(x)=-2\cdot \left((-\sin(x))\cdot \sin(x)+\cos(x)\cdot \cos(x)\right)=2\cdot \left((\sin(x))^2-(\cos(x))^2\right)$.
Die erste Ableitung muss für Extrema notwendig $0$ sein: $-2\cdot \cos(x)\cdot \sin(x)=0$, also ist
- entweder $\sin(x)=0~\Leftrightarrow~x=k\cdot \pi$
- oder $\cos(x)=0~\Leftrightarrow~x=\frac{\pi}2+k\cdot \pi$,
$k$ ist dabei eine ganze Zahl.
Setze nun diese Lösungen in die zweite Ableitung ein:
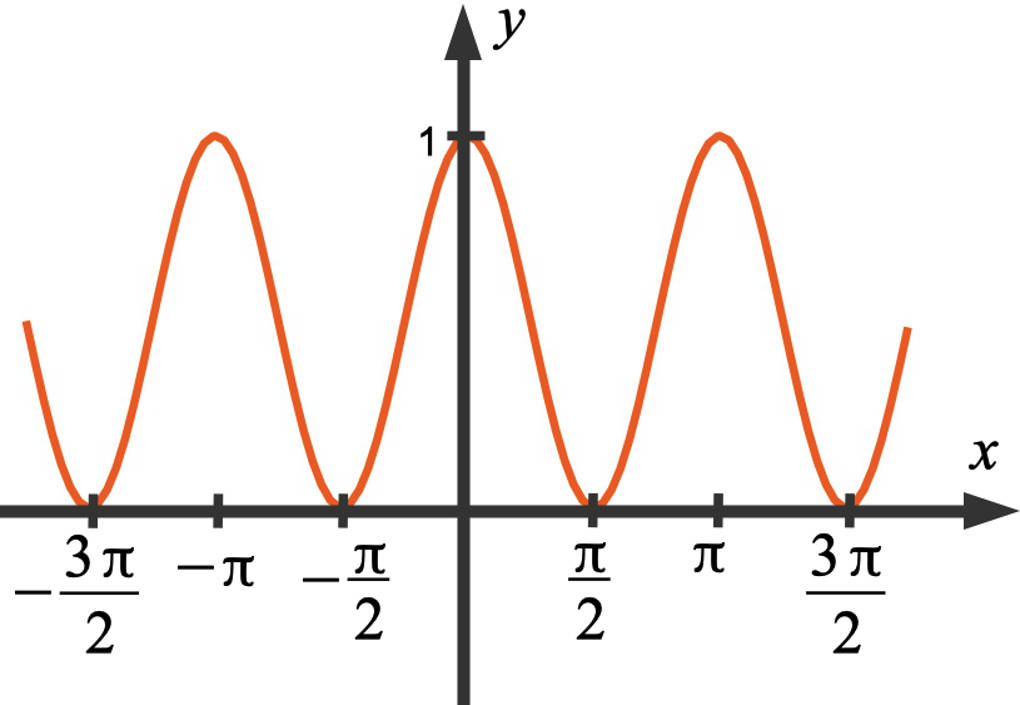
- $f''\left(k\cdot \pi\right)=-2\lt 0$: Das bedeutet, dass hier jeweils ein lokales Maximum vorliegt. Die $y$-Koordinate ist der Funktionswert von $f(x)$, also $1$.
- $f''\left(\frac{\pi}2+k\cdot \pi\right)=2\gt 0$: Hier liegt also jeweils ein lokales Minimum vor mit der $y$-Koordinate $0$.
Wendepunkte und Sattelpunkte
Im Folgenden benötigst du den trigonometrischen Pythagoras: $(\sin(x))^2+(\cos(x))^2=1$.
Diesen kannst du umformen zu $(\cos(x))^2)=1-(\sin(x))^2$.
Für die Wendepunkte betrachtest du nun die Gleichung $f''(x)=0$, also
$\begin{array}{rclll} 2\cdot \left((\sin(x))^2-(\cos(x))^2\right)&=&0&|&:2\\ (\sin(x))^2-(\cos(x))^2&=&0&|&\text{trigonometrischer Pythagoras}\\ 2(\sin(x))^2-1&=&0&|&+1\\ 2(\sin(x))^2&=&1&|&:2\\ (\sin(x))^2&=&\frac12&|&\sqrt{~~~}\\ \sin(x)&|&\pm\sqrt{\frac12} \end{array}$
So erhältst du $x=\frac{\pi}4+k\cdot \frac{\pi}2$, $k\in\mathbb{Z}$. Da diese Stellen immer zwischen zwei Extrema liegen, muss dort jeweils ein Wendepunkt vorliegen. Die zugehörige $y$-Koordinate erhältst du durch Einsetzen dieser Stellen in die Funktionsgleichung. Diese ist jeweils $\frac12$.
Der Funktionsgraph
Schließlich kannst du mit den bisherigen Ergebnissen den Funktionsgraphen zeichnen:
Alle Videos zum Thema
Videos zum Thema
Wurzelfunktionen – Kurvendiskussion (3 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Wurzelfunktionen – Kurvendiskussion (3 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung



 Wurzelfunktionen – Kurvendiskussion
Wurzelfunktionen – Kurvendiskussion
 Wurzelfunktionen: Kurvendiskussion – Übungen
Wurzelfunktionen: Kurvendiskussion – Übungen
 Trigonometrische Funktionen – Kurvendiskussion
Trigonometrische Funktionen – Kurvendiskussion









