Ortslinie und Ortskurve

Inhaltsverzeichnis zum Thema

• Was ist eine Funktionenschar?
• Was ist eine Ortskurve (Ortslinie)?
  • Eine zur $x$-Achse parallele Ortskurve
  • Eine zur $y$-Achse parallele Ortskurve
• Die Ortskurve der Tiefpunkte einer Parabelschar
  • Bestimmen der Extrempunkte und Umformen nach dem Parameter
  • Erstellen der Ortskurve eines bekannten Punktes
• Die Ortskurve am Beispiel einer biquadratischen Funktionenschar
  • Extrempunkte
  • Wendepunkte

Was ist eine Funktionenschar?

Um diesen Text zu lesen, solltest du bereits wissen, was eine Funktion ist. Es gibt eine unabhängige Variable (manchmal auch Argument genannt) $x$ und eine abhängige Variable $y=f(x)$ (wird auch Funktionswert genannt).

Wenn zusätzlich zu der Variablen noch ein Parameter in der Funktionsgleichung vorkommt, spricht man von einer Funktionenschar. Du erhältst dann nicht nur einen Funktionsgraphen, sondern einen Graphen für jeden Wert des Parameters. Der Parameter wird auch als Formvariable bezeichnet.

Was ist eine Ortskurve (Ortslinie)?

Eine Ortskurve (auch: Ortslinie) ist eine Kurve, die sich auf eine bestimmte Funktionenschar und eine Eigenschaft bezieht. Die Punkte, die auf der Ortskurve liegen, haben immer eine gemeinsame Eigenschaft im Bezug auf die Funktionenschar. Beispielsweise kann eine Ortskurve alle Extrempunkte einer Kurvenschar beinhalten. Du kannst die Ortskurve (bzw. Ortslinie) von verschiedenen Punkten einer Kurvenschar bestimmen.

Das bedeutet also:

• Auf der Ortskurve der Extrempunkte liegen alle Extrempunkte der Kurvenschar.
• Auf der Ortskurve der Wendepunkte liegen alle Wendepunkte der Kurvenschar.

Im Folgenden siehst du ein paar Beispiele.

Eine zur $x$-Achse parallele Ortskurve

Betrachte die quadratische Funktionenschar $f_a$ mit $f_a(x)=(x-a)^{2}+3$. Die Tiefpunkte der zugehörigen Parabelschar sind gegeben durch TP$(a|3)$. Die zugehörige Ortskurve lautet $y(x)=3$. Der zugehörige Funktionsgraph ist eine zur $x$-Achse parallele Gerade durch $y=3$.

Eine zur $y$-Achse parallele Ortskurve

Dieses Mal schauen wir uns die quadratische Funktionenschar $f_a$ mit $f_a(x)=(x-2)^{2}+a$ an. Die Tiefpunkte dieser Parabelschar sind gegeben durch TP$(2|a)$. Die zugehörige Ortskurve verläuft parallel zur $y$-Achse durch $x=2$. Eine zugehörige Funktionsgleichung kann hier nicht angegeben werden, da eine zur $y$-Achse parallele Gerade nicht der Graph einer Funktion sein kann.

Die Ortskurve der Tiefpunkte einer Parabelschar

Gegeben ist die quadratische Funktionenschar $f_a$ mit $f_a(x)=(x-2a)^{2}+a$ in der Scheitelpunktform.

Bestimmen der Extrempunkte und Umformen nach dem Parameter

Eine Möglichkeit, die Extrempunkte dieser Schar zu ermitteln, bietet die erste Ableitung. Diese lautet $f_a'(x)=2x-4a$ und muss gleich $0$ gesetzt werden. Das ergibt die Gleichung $2x-4a=0$. Forme diese Gleichung nach dem Parameter $a$ um:

$\begin{array}{rcl} 2x-4a & = & 0 \\ 4a & = &2x \\ a & = & \frac{1}{2} x\end{array}$

Setze nun diesen Wert für $a$ in die Funktionsgleichung ein:

$f_{\frac12 x}(x)=\left(x-2\cdot\frac12 x\right)^{2}+\frac12 x=0^{2}+\frac12 x=\frac12 x$

Dies ist die gesuchte Ortskurve. Die Funktionsgleichung der Ortskurve lautet $y(x)=\frac12 x$.

Im Folgenden siehst du zwei Möglichkeiten, wie du eine Ortskurve (bzw. Ortslinie) bestimmen kannst.

Erstellen der Ortskurve eines bekannten Punktes

Da die Schar $f_a$ mit $f_a(x)=(x-2a)^{2}+a$ in Scheitelpunktform vorliegt, kannst du den Scheitelpunkt (der in diesem Fall ein Tiefpunkt ist) direkt ablesen. Für den Scheitelpunkt gilt $S_a(2a|a)$. Jede Parabel dieser Schar ist nach oben geöffnet. Das bedeutet, dass der Scheitelpunkt immer der tiefste Punkt der jeweiligen Parabel ist.

Du weißt bereits, dass die Punkte $S_a(2a|a)$ die Extrempunkte der Kurvenschar sind. Nun kannst du auch wie folgt vorgehen:

• Forme die $x$-Koordinate $x=2a$ nach $a$ um. Mittels Division durch $2$ erhältst du $a=\frac12x$.
• Setze diesen Parameter nun in die $y$-Koordinate $y=a$ ein.
• So erhältst du $y(x)=\frac12 x$, die Ortskurve der Extrema.

Die Ortskurve am Beispiel einer biquadratischen Funktionenschar

Wir schauen uns hier noch ein weiteres Beispiel an.

Bestimmt werden sollen die Ortskurven bei ganzrationalen Funktionen sowohl für die Extrempunkte als auch für die Wendepunkte.

Gegeben ist die biquadratische Funktionenschar $f_a$ mit $f_a(x)=\frac12x^{4}-ax^{2}$ mit $a>0$. Beachte, dass die zugehörigen Funktionsgraphen achsensymmetrisch sind, da alle Exponenten gerade sind.

Zunächst bestimmst du die ersten beiden Ableitungen:

• $f_a'(x)=2x^{3}-2ax$
• $f_a''(x)=6x^{2}-2a$

Extrempunkte

Es muss $f_a'(x)=0$ gelten. Das ergibt also $2x^{3}-2ax=0$. Du kannst hier $2x$ ausklammern zu $2x\left(x^{2}-a\right)=0$. Wegen des Satzes vom Nullprodukt gilt:

• $x_1=0$ oder
• $x_{2;3}=\pm\sqrt a$

Für $x_1=0$ erhältst du mit $f_a''(0)=-2a<0$ und $f(0) = 0$ den lokalen Hochpunkt HP$(0|0)$. Dieser lokale Hochpunkt hängt nicht von $a$ ab, was bedeutet, dass alle Kurven der Schar diesen lokalen Hochpunkt gemeinsam haben.

Für $x_2=\sqrt a$ erhältst du wegen $f_a''(\sqrt a)=4a>0$ und $f_a(\sqrt a)=-\frac12a^{2}$ einen lokalen Tiefpunkt in $\left(\sqrt a|-\frac12a^{2}\right)$. Wegen der Achsensymmetrie gibt es einen weiteren Tiefpunkt in $\left(\sqrt a|-\frac12a^{2}\right)$

Nun kannst du die Ortskurve dieser Extrema bestimmen:

• Forme $x=\sqrt a$ nach $a$ um. Quadriere hierfür auf beiden Seiten der Gleichung $a=x^{2}$.
• Nun setzt du diesen Wert für $a$ in die $y$-Koordinate ein. So erhältst du die Ortskurve $y(x)=-\frac12\left(x^{2}\right)^{2}=-\frac12x^{4}$.

In dem folgenden Bild siehst du verschiedene Funktionsgraphen:

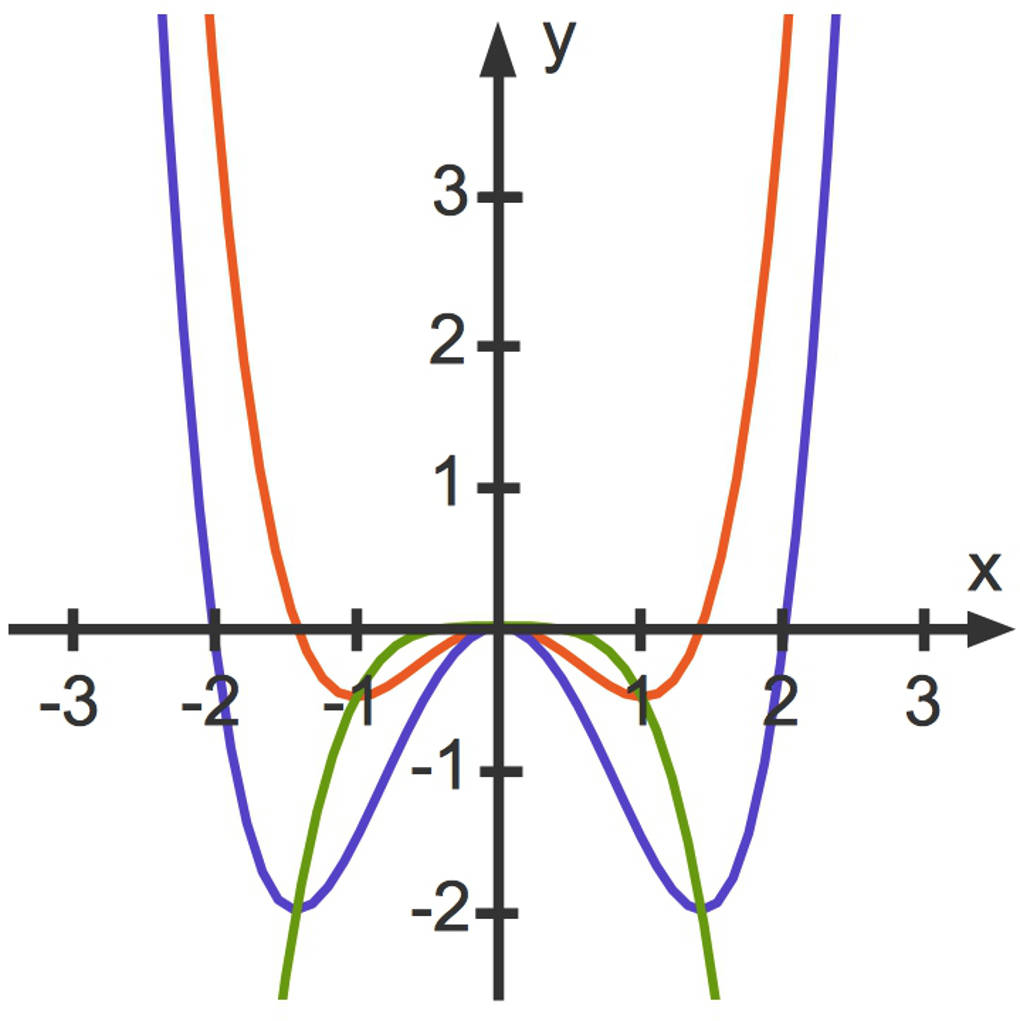
• Der rote Funktionsgraph ist der Graph der Funktion der Schar mit $a=1$
• Der blaue Funktionsgraph ist der Graph der Funktion der Schar mit $a=2$
• Der grüne Funktionsgraph zeigt die Ortskurve der Extrema.

Du kannst erkennen, dass die Extrema der beiden abgebildeten Funktionsgraphen auf dieser Ortskurve liegen.

Abschließend schauen wir uns noch die Ortskurve der Wendepunkte an:

Wendepunkte

Im Folgenden wird auf den Nachweis der hinreichenden Bedingung für Wendepunkte verzichtet. Für Wendepunkte muss gelten, dass die zweite Ableitung gleich $0$ ist. Du löst also die Gleichung $6x^{2}-2a=0$. Dies führt zu $x_{1,2}=\pm\sqrt{\frac a3}$. Es ist

$f_a\left(\sqrt{\frac a3}\right)=\frac12\left(\sqrt{\frac a3}\right)^{4}-a\left(\sqrt{\frac a3}\right)^{2}=-\frac5{18}a^2$

Du erhältst also die Wendepunkte WP$_a\left(\sqrt{\frac a3}|-\frac5{18}a^{2}\right)$ und WP$_a\left(-\sqrt{\frac a3}|-\frac5{18}a^{2}\right)$.

Jetzt formst du noch die $x$-Koordinate nach $a$ um zu $a=3x^{2}$ und setzt dies in die $y$-Koordinate ein:

$y(x)=-\frac5{18}\left(3x^{2}\right)^2=-\frac52x^4$

Dies ist die Ortskurve der Wendepunkte der biquadratischen Funktionenschar.