Kreiszahl Pi (π)
Die Zahl Pi beschäftigt Mathematiker schon seit vielen Jahrhunderten: Sie wird zur Umfang- und Flächenberechnung von Kreisen benötigt. Auch in vielen anderen Formeln taucht Pi auf.
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Die Geschichte der Zahl Pi
- Pi in der Bibel
- Das Näherungsverfahren von Archimedes
- Die Ludolphsche Zahl
- Pi heute
Die Geschichte der Zahl Pi
Die Geschichte der Zahl Pi reicht sehr weit zurück.
Pi in der Bibel
Bereits in der Bibel findet sich ein Text, aus welchem sich ein Näherungswert für Pi ablesen lässt:
"Und er machte das Meer, gegossen, zehn Ellen von seinem einen Rand bis zu seinem anderen Rand, ringsum rund und fünf Ellen seine Höhe; und eine Messschnur von dreißig Ellen umspannte es ringsherum."
Es handelt sich hier um einen Kreis mit dem Durchmesser $d=10$ Ellen. Dieser Kreis wird von einer Messschnur der Länge $30$ Ellen umspannt. Dies entspricht dem Umfang.
Eine Definition der Kreiszahl Pi, welche mit dem griechischen Buchstaben $\pi$ bezeichnet wird, ist das Verhältnis des Umfangs zu dem Durchmesser $d$ eines Kreises:
$\pi=\frac ud$.
Dies führt zu der folgenden Abschätzung:
$\pi\approx\frac{30~\text{Ellen}}{10~\text{Ellen}}=3$ .
Das Verhältnis von Umfang $u$ zum Durchmesser $d$ kannst du dir so vorstellen:
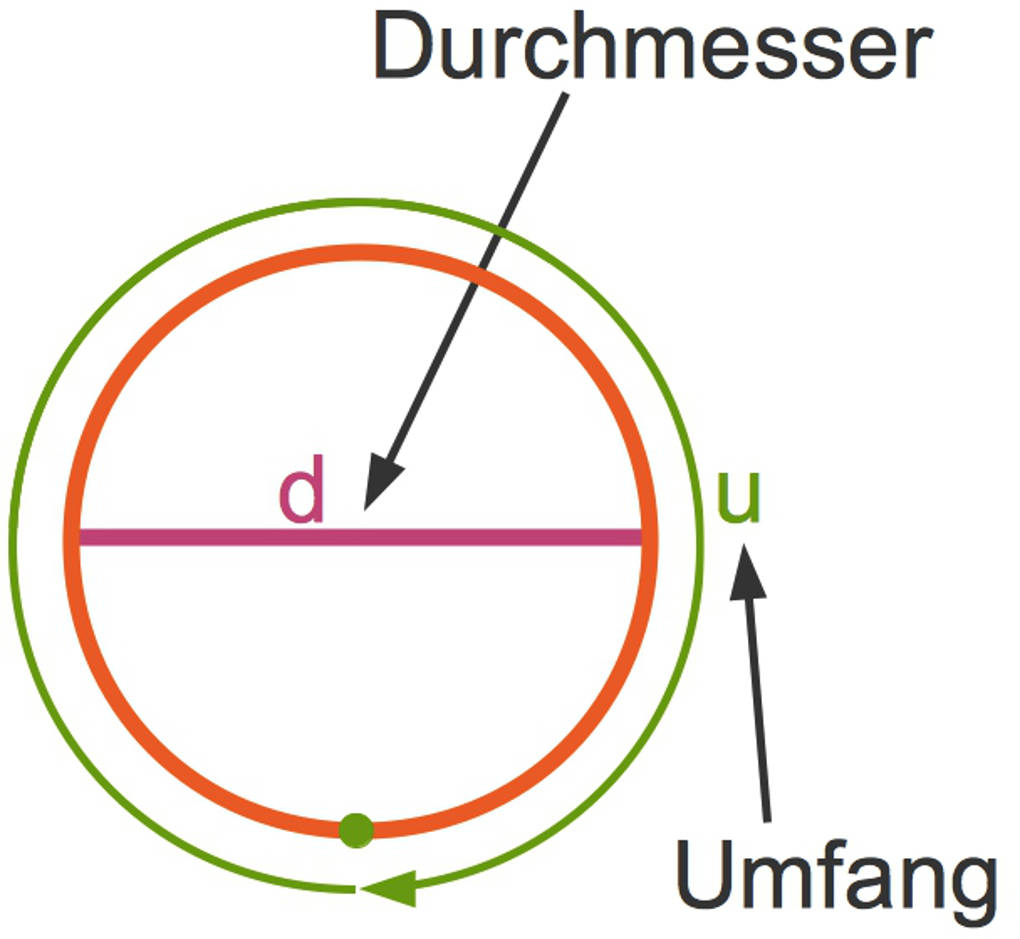
Wenn du einen Kreis mit dem Durchmesser $d=1$ Längeneinheit einmal komplett drehst, entspricht der Weg, welchen der grüne Punkt zurücklegt, dem Umfang des Kreises. Dieser Umfang beträgt gerade $\pi$ Längeneinheiten.
Die Abschätzung $3$ ist noch sehr ungenau. Im Laufe der Zeit, wurden immer mehr Nachkommastellen von $\pi$ berechnet.
Das Näherungsverfahren von Archimedes
Der griechische Mathematiker und Physiker Archimedes von Syrakus (287-212 v. Chr) hat mit Hilfe eines Näherungsverfahrens die Zahl $\pi$ etwas genauer abschätzen können.
Zur näherungsweisen Berechnung von $\pi$ verwendete Archimedes regelmäßige Vielecke:
- Ein Vieleck umschreibt den Kreis und ein weiteres Vieleck ist dem Kreis eingeschrieben.
- Das bedeutet, dass der Umfang des kleineren Vielecks kleiner ist als $\pi$ und $\pi$ wiederum kleiner als der Umfang des größeren Vielecks.
- Archimedes begann mit dem regelmäßigen Sechseck.

- Die Anzahl der Ecken verdoppelte Archimedes jeweils, so dass er ein $12-$, $24-$, $48-$ bis hin zu einem $96-$Eck für das Näherungsverfahren nutzte.
So gelangte er zu der folgenden Abschätzung:
$3,1408540\approx 3+\frac{10}{71}<\pi<3+\frac{10}{70}\approx 3,1428571$.
$\pi$ war damit bereits auf zwei Nachkommastellen genau bestimmt.
Die Ludolphsche Zahl
Der Mathematiker Ludolph van Ceulen (* 28. Januar 1540 in Hildesheim; † 31. Dezember 1610 in Leiden) führte das Näherungsverfahren nach Archimedes fort. Es gelang ihm mit Hilfe eines $262-$Ecks die ersten $35$ Stellen von $\pi$ zu berechnen. Als Belohnung für seine Arbeit wurde $\pi$ auch die Ludolphsche Zahl genannt. Auf von Ceulens Grabstein ist $\pi$ mit den $35$ Nachkommastellen eingraviert:
$\pi\approx 3,14159265358979323846264338327950288$.
Pi heute
Zur Zeit (Stand November 2016) ist die Kreiszahl $\pi$ bis auf $22,4$ Billionen Stellen berechnet.
Pi ist irrational
Was sind irrationale Zahlen? Irrationale Zahlen sind Dezimalzahlen, die weder endlich viele Nachkommastellen haben, noch periodische Dezimalzahlen sind. Das bedeutet, dass sich irrationale Zahlen nicht als Brüche schreiben lassen.
Die Kreiszahl $\mathbb{\pi}$ ist eine irrationale Zahl.
$\quad~~ \pi=3,141592653589793238462... $
Das bedeutet, dass selbst die oben bereits erwähnten $22,4$ Billionen Stellen noch nicht das Ende sind.
Die Verwendung von Pi
Nun schauen wir uns noch an, in welchen Bereichen $\pi$ genutzt werden kann. Du kannst dir merken: Immer wenn du es mit Kreisen zu tun hast, „ist die Kreiszahl $\pi$ nicht weit“.
Der Umfang und der Flächeninhalt eines Kreises
- Der Umfang eines Kreises lässt sich wie folgt berechnen: $u=\pi\cdot d=2\cdot \pi\cdot r$ Dabei ist $r$ der Radius des Kreises.
- Auch für den Flächeninhalt eines Kreises brauchst du $\pi$: $A=\pi\cdot r^2=\frac14\cdot \pi\cdot d^2.$
Die Oberfläche und das Volumen einer Kugel
- Hier siehst du die Formel für die Oberfläche einer Kugel: $O=4\cdot \pi\cdot r^2$.
- Das Volumen lässt sich berechnen mit: $V=\frac43\cdot \pi\cdot r^3$.
Die Mantelfläche und das Volumen eines Zylinders

Bei einem Zylinder sind sowohl die Grund- als auch die Deckfläche jeweils ein Kreis. Auch hier kommt in den verwendeten Formeln wieder die Kreiszahl $\pi$ vor:
- Die Mantelfläche, wobei $h$ die Höhe des Zylinders ist: $M=2\cdot \pi\cdot r\cdot h$.
- Das Volumen: $V=\pi\cdot r^2\cdot h$.
Du siehst, $\pi$ ist nicht nur sehr rätselhaft und sicher auch spannend, diese Zahl begegnet dir auch ständig. Abschließend lernst du noch die Zusammenhänge von Winkeln, dem Gradmaß, der Zahl $\pi$ und dem Bogenmaß kennen.
Das Bogenmaß
Ein Winkel kann in dem sogenannten Bogenmaß gegeben sein:
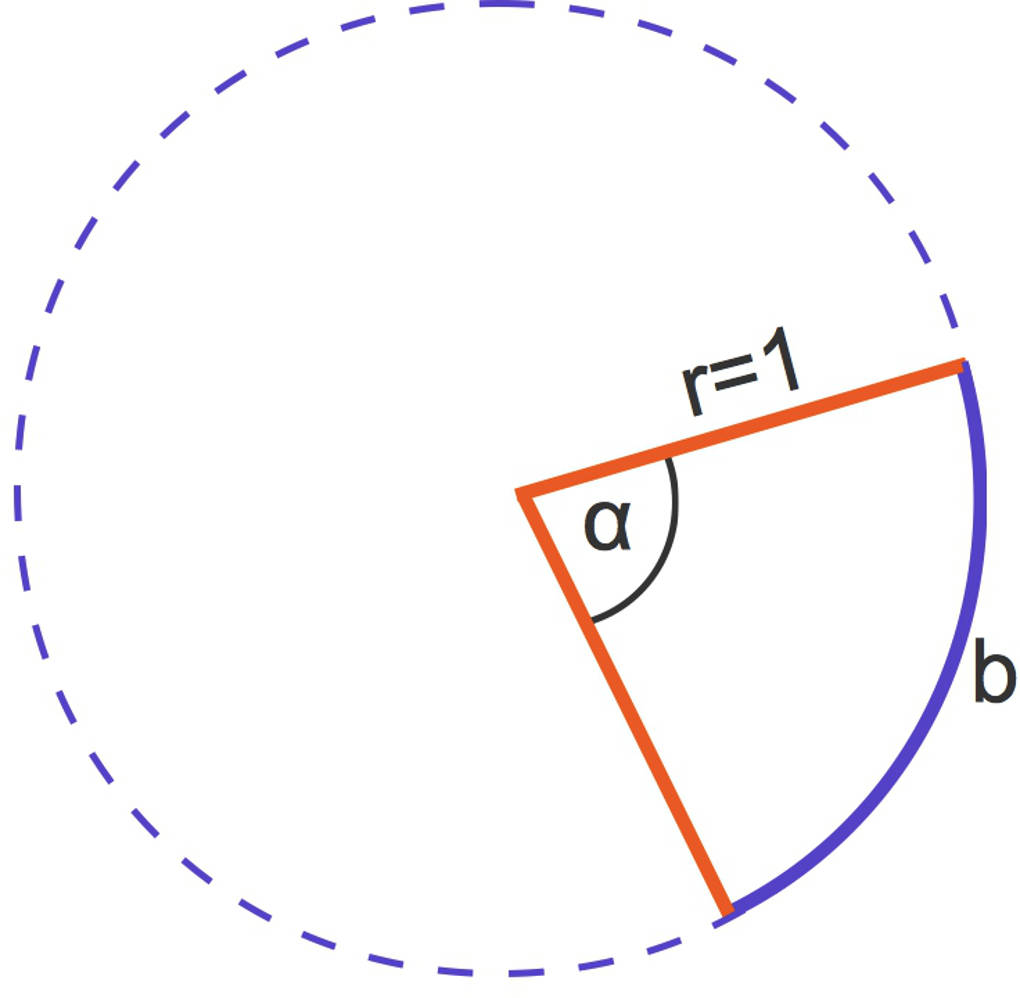
Hier siehst du einen Einheitskreis. Dieser hat den Radius $r=1$ und somit den Umfang $u=2\pi$. Zu dem eingezeichneten Winkel $\alpha$ gehört der blau gezeichnete Abschnitt des Kreisumfangs. Dieser wird als Kreisbogen oder kurz als Bogen bezeichnet. Die Maßeinheit eines Kreisbogens ist eine Längeneinheit.
Das bedeutet also, dass zum Beispiel der Vollwinkel $360^\circ$ dem Bogenmaß $2\pi$ entspricht, der gestreckte Winkel $180^\circ$ dem Bogenmaß $\pi$ und der rechte Winkel $90^\circ$ dem Bogenmaß $\frac{\pi}2$.
Alle Videos zum Thema
Videos zum Thema
Kreiszahl Pi (π) (3 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Kreiszahl Pi (π) (3 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung




 Kreiszahl Pi
Kreiszahl Pi
 Kreise und die Kreiszahl Pi (π)
Kreise und die Kreiszahl Pi (π)
 Kreiszahl Pi – Näherungsverfahren von Archimedes
Kreiszahl Pi – Näherungsverfahren von Archimedes









