Technische Anwendung des magnetischen Feldes
Halleffekt; Massenspektroskopie; Zyklotron; MHD-Generator; Elektronenmikroskop; Synchrotron
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
Das Besondere an magnetischen Feldern
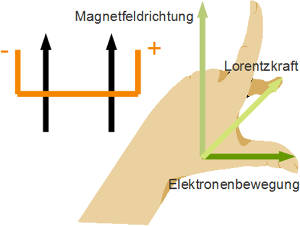
Du hast bestimmt schon einiges über die Eigenschaften von magnetischen Feldern gehört. Eine Besonderheit von magnetischen Feldern ist, dass sie bewegte, geladene Teilchen ablenken. Dies kommt durch die Lorentzkraft zustande. Wenn sich ein geladenes Teilchen senkrecht zu einem Magnetfeld bewegt, dann wird es durch die konstante Ablenkung durch die Lorentzkraft auf eine Kreisbahn gelenkt. Dieser Effekt wird in verschiedenen Anwendungen nutzbar gemacht.
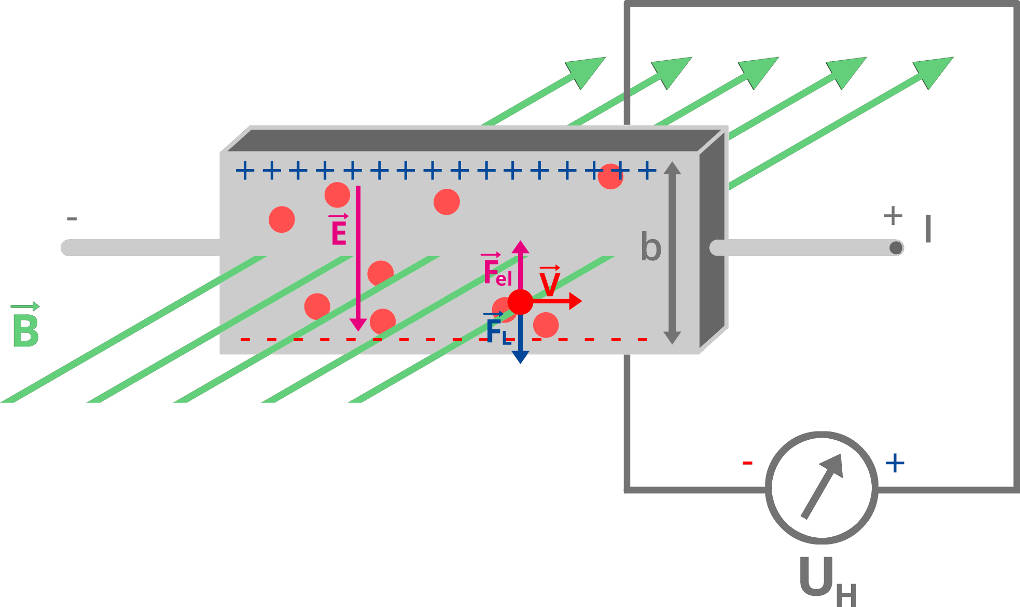
Der Hall-Effekt
Der Hall-Effekt bezeichnet das Auftreten einer Spannung in einem stromdurchflossenen Leiter, der sich in einem Magnetfeld befindet. Die Elektronen werden durch die Lorentzkraft zur Seite abgelenkt. Es bildet sich an einer Seite des Leiters ein Elektronenüberschuss. So entsteht ein elektrisches Feld senkrecht zur Richtung von Magnetfeld und Strom. Die Kraft des elektrischen Feldes wirkt dann der des magnetischen Feldes entgegen und weitere Elektronen durchqueren den Leiter unabgelenkt.
Das Zyklotron
Ein Zyklotron ist ein Kreisbeschleuniger. In diesem werden geladene Teilchen wiederholt beschleunigt und durch ein Magnetfeld auf einer Spiralbahn gehalten.
Aufbau und Funktionsweise
Das Zyklotron besteht aus zwei Duanten, die senkrecht von einem Magnetfeld durchsetzt sind. Ein Duant ist ein D-förmiger und an der geraden Seite offener Hohlkörper aus Metall. Du kannst ihn dir wie eine flache, halbierte Konservendose vorstellen. In der Mitte des Zyklotrons befindet sich eine Ionenquelle zur Freisetzung geladener Teilchen. Zwischen den Duanten liegt eine hochfrequente Wechselspannung an. Diese dient der Beschleunigung der geladenen Teilchen im Spalt. In den Duanten wirkt nur das magnetische Feld.
Die Teilchen werden dann bei jedem Durchgang durch den Spalt beschleunigt und beschreiben ansonsten, abgelenkt durch die Lorentzkraft, Halbkreisbahnen. Durch die immer wiederkehrende Beschleunigung wächst der Radius des Halbkreises mit jedem Umlauf. Die Teilchen bewegen sich deswegen bis zum Auslass auf einer spiralförmigen Bahn. Am Auslass verlassen die Teilchen das Zyklotron.
Bei sehr schnellen Teilchen muss die relativistische Masse einbezogen werden. Die Frequenz der Wechselspannung muss dann so angepasst werden, dass die Beschleunigung gleichmäßig bleibt. Ein Zyklotron mit dieser Eigenschaft heißt Synchro-Zyklotron.
Das Synchroton
Das Synchroton ist eine Weiterentwicklung des Zyklotrons. Es kann auch bei sehr hohen Teilchengeschwindigkeiten eingesetzt werden. Die Funktionsweise ist ähnlich. Auch hier werden die Teilchen durch ein elektrisches Feld beschleunigt und durch ein magnetisches Feld auf ihre Bahn gelenkt.
Aufbau des Synchrotons
Das Synchroton besteht aus einem ringförmigen Tunnel, dem Torus. Er wird von Magnetfeldern eingerahmt, mit denen geladene Teilchen verschiedenster Geschwindigkeiten genau auf der kreisförmigen Mittellinie gehalten werden können. Dazwischen befinden sich elektrische Felder zur Beschleunigung der Teilchen. Die verschiedenen Felder sind so synchronisiert, dass auch die relativistische Massezunahme einbezogen wird. Magnetische und elektrische Felder müssen dabei mit zunehmender Geschwindigkeit der Teilchen gezielt verstärkt werden.
Das Synchroton ist von einem Ein- und einem Auslass durchbrochen. In letzterem kann ein Target gehalten werden, auf das die beschleunigten Teilchen treffen. Es können dabei verschiedenste physikalischen Effekte beobachtet und erforscht werden.
Das Massenspektrometer
Das Massenspektrometer wird genutzt, um die Masse von Atomen und Molekülen zu bestimmen. Mit einem Geschwindigkeitsfilter, der aus einem elektrischen Feld und einem senkrecht dazu stehenden Magnetfeld besteht, werden nur geladene Teilchen einer bestimmten Geschwindigkeit durchgelassen. Alle anderen Teilchen werden abgelenkt. Anschließend treten die bewegten, geladenen Teilchen in ein Magnetfeld ein. Dort bewegen sie sich auf einer Kreisbahn. Der Radius dieser Kreisbahn kann gemessen und damit die Masse des Teilchens ermittelt werden.
MHD-Generator
Der Magnetohydrodynamischer Generator, kurz auch MHD-Generator, wandelt thermische Energie und Bewegungsenergie mithilfe eines Magnetfeldes in elektrische Energie um. Die zugeführte Energie stammt dabei von einem Plasma-Strom. In einem Plasma-Strom sind Elektronen und Ionen nicht mehr aneinander gekuppelt. Im Magnetfeld werden die Ladungen je nach Vorzeichen durch die Lorentzkraft in entgegengesetzte Richtungen abgelenkt. Es erfolgt somit eine Ladungstrennung, wodurch wiederum ein elektrisches Feld entsteht.
Alle Videos und Lerntexte zum Thema
Videos und Lerntexte zum Thema
Technische Anwendung des magnetischen Feldes (8 Videos, 2 Lerntexte)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Technische Anwendung des magnetischen Feldes (8 Arbeitsblätter)
-
 Spezifische Ladung des Elektrons – Ermittlung mit Fadenstrahlrohr und Helmholtzspule
PDF anzeigen
Spezifische Ladung des Elektrons – Ermittlung mit Fadenstrahlrohr und Helmholtzspule
PDF anzeigen -
 Hall-Effekt – Wirkung der Kräfte im Leiter
PDF anzeigen
Hall-Effekt – Wirkung der Kräfte im Leiter
PDF anzeigen -
 Zyklotron
PDF anzeigen
Zyklotron
PDF anzeigen -
 Zyklotron – Überblick
PDF anzeigen
Zyklotron – Überblick
PDF anzeigen -
 Zyklotron – Übungen
PDF anzeigen
Zyklotron – Übungen
PDF anzeigen -
 Synchrotron
PDF anzeigen
Synchrotron
PDF anzeigen -
 MHD-Generator
PDF anzeigen
MHD-Generator
PDF anzeigen -
 Massenspektrometer
PDF anzeigen
Massenspektrometer
PDF anzeigen
Beliebteste Themen in Physik
- Temperatur
- Schallgeschwindigkeit
- Dichte
- Drehmoment
- Transistor
- Lichtgeschwindigkeit
- Elektrische Schaltungen – Übungen
- Galileo Galilei
- Rollen- Und Flaschenzüge Physik
- Radioaktivität
- Aufgaben zur Durchschnittsgeschwindigkeit
- Lorentzkraft
- Beschleunigung
- Gravitation
- Ebbe und Flut
- Hookesches Gesetz Und Federkraft
- Elektrische Stromstärke
- Elektrischer Strom Wirkung
- Reihenschaltung
- Ohmsches Gesetz
- Freier Fall
- Kernkraftwerk
- Reflexionsgesetz: Ebener Spiegel – Übungen
- Was sind Atome
- Aggregatzustände
- Infrarot, Uv-Strahlung, Infrarot Uv Unterschied
- Isotope, Nuklide, Kernkräfte
- Transformator
- Lichtjahr
- Si-Einheiten
- Fata Morgana
- Gammastrahlung, Alphastrahlung, Betastrahlung
- Kohärenz Physik
- Mechanische Arbeit
- Schall
- Elektrische Leistung
- Dichte Luft
- Ottomotor Aufbau
- Kernfusion
- Trägheitsmoment
- Heliozentrisches Weltbild
- Energieerhaltungssatz Fadenpendel
- Linsen Physik
- Ortsfaktor
- Interferenz
- Diode und Photodiode
- Wärmeströmung (Konvektion)
- Schwarzes Loch
- Frequenz Wellenlänge
- Elektrische Energie






















