Hall-Effekt – Wirkung der Kräfte im Leiter
Der Hall-Effekt ist ein faszinierendes Phänomen des Elektromagnetismus, das in Magnetsonden verwendet wird. Erfahre, unter welchen Bedingungen der Hall-Effekt auftritt und wie er zur Messung von Magnetfeldern genutzt wird. Interessiert? Du wirst all das und mehr im folgenden Text entdecken!
- Der Hall-Effekt in der Physik
- Hall-Effekt – Definition
- Hall-Effekt – Erklärung
- Herleitung der Hall-Spannung
- Hall-Effekt – Anwendung


in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.

Grundlagen zum Thema Hall-Effekt – Wirkung der Kräfte im Leiter
Der Hall-Effekt in der Physik
Der Hall-Effekt ist ein Phänomen aus dem Bereich des Elektromagnetismus, das zum Beispiel in Magnetsonden genutzt wird. Wir wollen uns im Folgenden damit beschäftigen, unter welchen Bedingungen man den Hall-Effekt beobachten kann und wie man mit seiner Hilfe ein Magnetfeld vermisst.
Hall-Effekt – Definition
Wenn man durch einen elektrischen Leiter, der sich in einem Magnetfeld befindet, einen Strom fließen lässt, tritt senkrecht zur Stromrichtung und zur Richtung der Magnetfeldlinien eine Spannung auf. Diese Spannung wird Hall-Spannung $U_H$ genannt.
Hall-Effekt – Erklärung
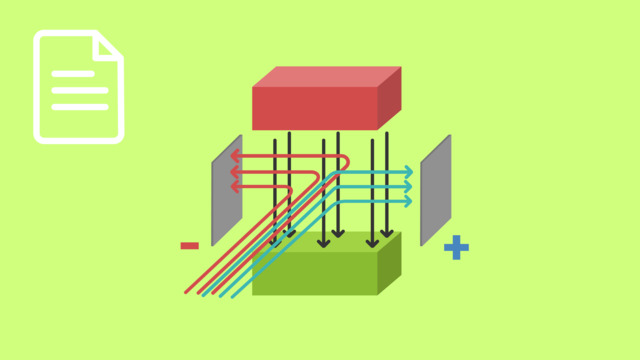
Wir wollen zunächst phänomenologisch verstehen, weshalb es zum Auftreten der Hall-Spannung kommt, um im Anschluss eine Formel für die Spannung herzuleiten. Wir betrachten zunächst die folgende Skizze.
Durch ein Plättchen der Länge $l$ und der Breite $b$ fließt ein elektrischer Strom $I$. Das Plättchen befindet sich in einem Magnetfeld $\vec{B}$, dessen Feldlinien senkrecht auf dem Plättchen und somit senkrecht auf der Stromrichtung stehen.
Wir wissen bereits, dass wir den Stromfluss als die gerichtete Bewegung von Ladungsträgern beschreiben können. In diesem Fall nehmen wir an, dass als Ladungsträger ausschließlich Elektronen vorkommen. Sobald sich Elektronen durch das Plättchen bewegen, das senkrecht im Magnetfeld steht, wirkt auf sie die Lorentzkraft $\vec{F}_L$. Die Richtung der Lorentzkraft können wir mithilfe der Linke-Hand-Regel bestimmen – in unserem Fall zeigt die Kraft nach rechts. Das bedeutet, dass die Elektronen, die durch das Plättchen wandern, nach rechts abgelenkt werden. Dadurch entsteht auf der rechten Seite des Plättchens ein Elektronenüberschuss und somit ein elektrisches Feld $E$. Folglich liegt eine elektrische Spannung $U$ zwischen linker und rechter Außenfläche des Plättchens an.
Durch das elektrische Feld wirkt wiederum eine Kraft $\vec{F}_E$ auf die Elektronen, die nach links beschleunigt werden. Die Kraft $\vec{F}_E$ wirkt also der Lorentzkraft entgegen. Sobald die Lorentzkraft und die Kraft durch das elektrische Feld gleich groß sind, sich also ein Gleichgewicht eingestellt hat, entspricht die Spannung zwischen den Außenflächen des Plättchens der Hall-Spannung $U_H$.
Herleitung der Hall-Spannung
Wir wollen nun unsere Erkenntnisse über das Zustandekommen der Hall-Spannung nutzen, um eine Formel zu ihrer Berechnung herzuleiten. Wir nutzen dabei aus, dass alle relevanten Größen senkrecht aufeinander stehen. Wir müssen daher nicht mit Vektoren rechnen, sondern können ausschließlich die Beträge der Kräfte und des Magnetfelds betrachten.
Wir wissen, dass auf einen stromdurchflossenen Leiter im Magnetfeld die Lorentzkraft
$F_L=I\cdot l \cdot B = q\cdot E = F_{E}$
Im Gleichgewicht wird das elektrische Feld gerade durch die Hall-Spannung zwischen den Seitenflächen hervorgerufen.
Wir können uns das Feld außerdem wie das Feld eines Plattenkondensators vorstellen. Dann gilt:
$E = \frac{U_H}{b}$
Dabei ist $U_H$ die Hall-Spannung und $b$ die Breite des Plättchens.
Die Ladung $q$ in der Formel für das Kräftegleichgewicht setzt sich aus der Anzahl $x$ aller einzelnen Ladungsträger mit Ladung $e$ innerhalb des Plättchens zusammen. Wir können also schreiben:
$I\cdot l \cdot B = x\cdot e \cdot \frac{U_H}{b}$
Da wir $x$ nicht kennen, müssen wir die Anzahl der Ladungsträger durch andere Größen ausdrücken. Wir nutzen dazu die Elektronendichte $n$. Diese gibt an, wie viele Elektronen pro Volumen vorhanden sind, und ist eng mit der Leitfähigkeit des verwendeten Materials verknüpft. Um die Anzahl der Ladungsträger zu erhalten, müssen wir die Elektronendichte mit dem Volumen multiplizieren. Also:
$x = n \cdot V = n\cdot b\cdot l \cdot d$
Dabei sind $b$, $l$ und $d$ die Breite, Länge und Dicke des Plättchens. Diesen Term für $x$ setzen wir nun in die Formel für das Kräftegleichgewicht ein:
$I\cdot l\cdot B = n\cdot b\cdot l\cdot d \cdot e\cdot \frac{U_H}{b}$
Jetzt können wir einige Größen kürzen:
$I\cdot B = n\cdot d\cdot e \cdot U_H$
Wir stellen die vereinfachte Formel nach der Hall-Spannung $U_H$ um:
$U_H = \frac{1}{n\cdot e} \frac{I\cdot B}{d}$
Den Term $\frac{1}{n\cdot e}$ können wir zu der sogenannten Hall-Konstanten $A_H$ zusammenfassen. [Achtung! Die Hall-Konstante ist nur dann als
In unserem Fall ergibt sich beim Hall-Effekt die folgende Formel für die Hall-Spannung:
$U_H = A_H \cdot \frac{I\cdot B}{d}$
Hall-Effekt – Anwendung
Eine Anwendung des Hall-Effekts ist das Messen der magnetischen Flussdichte. Wenn wir noch einmal einen Blick auf die Formel für die Hall-Spannung werfen, sehen wir, dass sie proportional zur magnetischen Flussdichte $B$ ist. Wenn wir die Formel nach $B$ umstellen, erhalten wir die folgende Gleichung:
$B = \frac{U_H\cdot d}{A_H\cdot I}$
Die Stärke des Stroms $I$ und die Dicke des Plättchens $d$ können wir selbst festlegen. Die Hall-Konstante $A_H$ ist materialspezifisch. Wenn wir für das Plättchen ein Material wählen, dessen Hall-Konstante wir kennen, müssen wir lediglich die Hall-Spannung $U_H$ messen und können die magnetische Flussdichte $B$ berechnen.
Messgeräte, die den Hall-Effekt nutzen, um die magnetische Flussdichte zu bestimmen, werden auch Hall-Sonden genannt.
Hall-Effekt – Zusammenfassung
Wir fassen die wichtigsten Erkenntnisse zum Hall-Effekt noch einmal zusammen:
- Der Hall-Effekt tritt in stromdurchflossenen Leitern auf, die sich in einem Magnetfeld befinden.
- Senkrecht zu Magnetfeld und Stromrichtung tritt eine Spannung auf.
- Die Höhe der Spannung ist proportional zur magnetischen Flussdichte des Magnetfelds.
- Der Hall-Effekt findet unter anderem Anwendung in Hall-Sonden zur Vermessung von Magnetfeldern.
Transkript Hall-Effekt – Wirkung der Kräfte im Leiter
Hallo und herzlich willkommen zu Physik mit Kalle. Wir machen heute aus dem Gebiet Elektrizität und Magnetismus den Hall-Effekt. Für dieses Video solltet ihr bereits den Film über die Lorentzkraft gesehen haben. Wir lernen heute, was der Hall-Effekt ist, wie man die Formel für die Hallspannung herleiten kann und wie man dieses Prinzip auch für andere physikalische Probleme nutzen kann, zum Beispiel den fahrenden Zug. Als Hall-Effekt bezeichnet man das Auftreten einer Spannung, die wir UH nennen, in einem stromdurchflossenen Plättchen, das sich in einem Magnetfeld befindet. Dabei gilt: Die Hallspannung UH ist senkrecht zur Strom- und Magnetfeldrichtung. Damit wir uns das besser vorstellen können, wollen wir das Plättchen einmal kurz aufzeichnen. Wir haben gerade gehört, dass die Hallspannung senkrecht zur Magnetfeld- und zur Stromrichtung ist. Wenn wir also nun eine Spannungsquelle oben und unten an unser Plättchen anschließen und dann ein Magnetfeld in den Bildschirm hineinrichten, dann müsste sich eine Spannung zwischen der linken und der rechten Seite des Plättchens aufbauen. Und genau das passiert auch. Da die Hallspannung senkrecht zur Magnetfeld- und Stromrichtung ist und die Lorentzkraft, wie wir uns erinnern, ebenfalls senkrecht zur Strom- und Magnetfeldrichtung ist, wollen wir doch einmal sehen, ob wir mit deren Hilfe nicht eine Formel für die Hallspannung herleiten können. Als Erstes sehen wir uns einmal genauer an, was in unserem Plättchen eigentlich passiert. Wir schließen die Spannungsquelle so an, dass die physikalische Stromrichtung von unten nach oben zeigt. Wir richten das Magnetfeld wieder in den Bildschirm hinein und dadurch sollte auf unsere Ladungsträger, nehmen wir mal an, es handelt sich dabei um Elektronen, die Lorentzkraft wirken. Denn, wie wir uns erinnern, fließender Strom bedeutet bewegte Ladungsträger und auf bewegte Ladungen wirkt die Lorentzkraft. Mithilfe der Linke-Hand-Regel stellen wir fest, unsere Elektronen sollten nach rechts auslenkt werden. Dadurch ergibt sich ein Überschuss von negativen Ladungen auf der rechten Seite und ein Überschuss an positiven Ladungen auf der linken Seite. Und das baut wiederum ein elektrisches Feld auf, das ebenfalls auf unsere Elektronen wirkt. Dieses elektrische Feld wiederum übt nun eine Kraft aus, die unsere Elektronen in die entgegengesetzte Richtung drückt. Wir merken uns also: Die Ladungsträger werden von der Lorentzkraft im Plättchen so lange verschoben, bis die dadurch entstehende elektrische Kraft imstande ist, die Lorentzkraft aufzuheben. Sobald dies der Fall ist, können wir links und rechts am Plättchen ein Spannungsmessgerät anschließen und die Hallspannung ablesen. Dann wollen wir einmal unsere beiden Kräfte hinschreiben, die wir, denn das klingt nach einem guten Ansatz, gleichsetzen werden. Wir kennen bereits die Formel, die uns die Summe der Lorentzkräfte auf die bewegten Ladungsträger in einem stromdurchflossenen Leiter gibt. Diese Formel ist: FL=I×l×B (Lorenzkraft=Stromstärke×Länge des Leiters×magnetische Flussdichte). Die Kraft auf eine Ladung im elektrischen Feld FEl=q×E, also Ladung×Feldstärke, wobei Ladung in dem Fall die summierte Ladung aller von uns betrachteten Elektronen heißt. Das heißt, es ist eine noch unbekannte Zahl x×die Elementarladung×die Feldstärke. Und die Feldstärke e ist natürlich die Hallspannung UH durch die Breite unseres Plättchens. Als Nächstes müssen wir unsere Zahl x ein wenig besser schreiben. Dazu formen wir sie um und setzen x=n×V (Eletronendichte mal Volumen). Die Elektronendichte ist eine Größe, die mir angibt, wie viele Elektronen zum Beispiel in 1m³ sind. Wenn ich die Elektronendichte nun mit einem bestimmten Volumen malnehme, bekomme ich als Ergebnis genau heraus, wie viele Elektronen sich in diesem Volumen befinden würden. Nun setze ich die beiden Gleichungen gleich und kann schreiben: Ι×l×B=n×V×e×(UH/b). Und da das Volumen unseres Plättchens ja genau Länge×Breite×Dicke ist, kann ich auch schreiben: =n×l×b×d×e×(UH/b). Damit kürzen sich sofort Länge und Breite aus meiner Gleichung heraus und ich kann nach der Hallspannung umstellen und erhalte: UH=(Ι×B)/(n×d×e). Diese Formel gilt jedoch nur für Stoffe, in denen die Elektronen die alleinigen Ladungsträger sind. Allgemein lautet die Formel für die Hallspannung: UH=AH×(I×B)/d (AH nennt man die Hallkonstante). Das heißt, für unseren Fall, in dem die Elektronen die alleinigen Ladungsträger sind, ist die Hallkonstante AH=1/(n×e). Für andere Stoffe, zum Beispiel Halbleiter, ist dies anders. Als Letztes wollen wir uns nun an einem Beispiel ansehen, wie wir dieses Prinzip des Kräftegleichgewichts auch auf Aufgaben anwenden können, die auf den ersten Blick überhaupt nichts mit der Hallspannung zu tun haben. Gegeben ist folgende Aufgabe: Ein Zug, Geschwindigkeit v=100km/h, fährt von Nord nach Süd durch das Erdmagnetfeld, Flussdichte B=40μT, Winkel zu den Schienen=45°. Welche Spannung wird zwischen den Schienen gemessen, wenn sie einen Abstand d von 1m haben? Auf den ersten Blick könnte man denken, dass hier kein Strom fließt und das damit überhaupt nichts mit dem Hall-Effekt zu tun hat. Auf den zweiten Blick aber werdet ihr sehen, dass die Elektronen, die sich frei in der Achse befinden, mit 100km/h durch das Magnetfeld der Erde gezogen werden. Dabei spielt natürlich nur der senkrecht zur Geschwindigkeit stehende Teil des Magnetfelds eine Rolle. Das heißt, gleich merken, den werden wir nachher ausrechnen müssen. Durch die Lorentzkraft werden also auch hier die freien Ladungsträger in der Achse so weit verschoben, bis das dadurch entstehende elektrische Feld die Lorentzkraft kompensiert. Wir setzen also wieder Lorentzkraft und elektrische Kraft gleich. Unser Ansatz ist: q×v×B=q×e. Und wie vorhin ist e wieder U/d. Dadurch kürzt sich die Ladung heraus und wenn wir nun für B den Teil B senkrecht einsetzen, den wir mit =B×cosα ausrechnen können, ergibt sich: U=v×d×B×cosα. Wenn ich einsetze, erhalte ich also für die Spannung: 100km/h×1m×40μT×cos45°. Wenn ich mir das ein wenig kürzungsfreudiger umforme, erhalte ich: =100/3,6m/s×1m×4×10^-5×Vs/m²×0,707, denn das ist der cos45°. Wie ihr seht, kürzen sich alle Einheiten bis auf die Volt heraus, und das ist gut, ich will ja auch eine Spannung haben. Das Ergebnis ist dann: 7,86×10^-4 V. Wir wollen noch einmal wiederholen, was wir heute gelernt haben. Hall-Effekt nennt man das Auftreten einer Spannung in einem stromdurchflossenen Plättchen, das sich in einem Magnetfeld befindet. Diese Spannung ist senkrecht zur Strom- und Magnetfeldrichtung. Der Hall-Effekt wird verursacht durch die Lorentzkraft. Die Formel zur Berechnung der Hallspannung kann man also durch Gleichsetzen der Lorentzkraft und der elektrischen Kraft herleiten. Dieses Prinzip kann man auch zur Lösung vieler anderer physikalischer Probleme nutzen. So, das war es schon wieder für heute. Ich hoffe, ich konnte euch helfen. Vielen Dank fürs Zuschauen, vielleicht bis zum nächsten Mal. Euer Kalle
Hall-Effekt – Wirkung der Kräfte im Leiter Übung
-
Gib an, was man unter dem Hall-Effekt versteht.
TippsWelche physikalische Größe besitzt das Formelzeichen $U$?
LösungLässt man einen Strom durch ein dünnes Plättchen in einem Magnetfeld fließen, so werden die Elektronen durch die Lorentzkraft abgelenkt und sammeln sich am seitlichen Rand des Plättchens. Dadurch entsteht ein elektrisches Feld und eine Spannung zwischen den Rändern des Plättchens. Durch das elektrische Feld wirkt auf die Elektronen eine zweite Kraft, die der Lorentzkraft entgegenwirkt. Diesen Effekt nennt man Hall-Effekt.
Als Hall-Effekt bezeichnet man somit das Auftreten einer Spannung $U_H$ in einem stromdurchflossenen Plättchen, das sich in einem Magnetfeld befindet.
-
Gib an, in welche Richtung die Elektronen im Bild jeweils abgelenkt werden.
TippsNutze die Linke-Hand-Regel.
Die Linke-Hand-Regel nutzt du folgendermaßen:
Der Daumen zeigt die Richtung des Stroms (und zwar von - nach +) an und stellt die Ursache dar. Der Zeigefinger gibt die Richtung des magnetischen Feldes an. Der Mittelfinger zeigt dann in die Richtung der Kraft (die Wirkung).
Was ist der Unterschied zwischen der technischen und der physikalischen Stromrichtung?
LösungUm die Aufgabe lösen zu können, solltest du die Linke-Hand-Regel (LHR) nutzen. Diese hilft dir herauszufinden, in welche Richtung die Lorentzkraft wirkt.
Die LHR nutzt du wie folgt: Der Daumen zeigt die Richtung des Stroms (und zwar von - nach +) an und stellt die Ursache dar. Der Zeigefinger gibt die Richtung des magnetischen Feldes an. Der Mittelfinger zeigt dann in die Richtung der Kraft (die Wirkung).
Somit wirkt die Lorentzkraft nach rechts.
Die Bewegung auf Grundlage des Hall-Effekts wirkt der Lorentzkraft genau entgegen, also nach links.
Bei der Betrachtung des Hall-Effektes solltest du wissen, dass sich die technische und die physikalische Stromrichtung unterscheiden. Hierbei gilt:
Die technische Stromrichtung geht von plus nach minus.
Die physikalische Stromrichtung geht von minus nach plus.
-
Gib die Herleitung zur Gleichung der Hall-Spannung an.
TippsUm die Hall-Spannung zu ermitteln, wird ein Kräfte-Gleichgewicht genutzt.
$F_L=F_{El}$
LösungUm die Hall-Spannung zu ermitteln, wird ein Kräfte-Gleichgewicht genutzt. Denn wenn die Elektronen sich vollständig ausgelenkt haben, ist die Lorentzkraft genauso groß wie die elektrische Kraft auf Grundlage des Hall-Effekts. Somit ist der erste Schritt:
$F_L=F_{El}$.
An dieser Stelle setzen wir die Definitionen beider Kräfte ein:
$I\cdot l \cdot B=q\cdot E$.
Die Lorentzkraft ist jedoch noch etwas spezieller auszudrücken. Dazu nutzen wir: $F_{El}=q\cdot E=x \cdot e \frac{U_H}{b}= n\cdot V \cdot e \frac{U_H}{b}$.
Diese Umformulierung der Lorentzkraft setzen wir in das Kräftegleichgewicht ein: $I\cdot l \cdot B=n\cdot l\cdot b \cdot d \cdot e \frac{U_H}{b}$.
Einige Variablen können an dieser Stelle gekürzt werden: $I \cdot B=n \cdot d \cdot e \cdot U_H$.
Diese Gleichung ist nach der gesuchten Hall-Spannung umzustellen: $U_H=\frac{I \cdot B}{n \cdot d \cdot e}$.
-
Gib die Formelzeichen zu den physikalischen Größen an.
Tipps$I$, $B$ und $e$ sind drei zentrale Größen der Elektrizitätslehre.
$U_H$ ist die zu berechnende Größe.
LösungIn der Gleichung zur Berechnung der Hall-Spannung $U_H=\frac{I \cdot B}{n \cdot d \cdot e}$ finden sich sechs verschiedene physikalische Größen.
Offensichtlich ist $U_H$ die Hall-Spannung, da diese mit der Gleichung ja zu berechnen ist.
$I$, $B$ und $e$ sind wiederum drei zentrale Größen der Elektrizitätslehre: $I$ ist die Stromstärke, $B$ die magnetische Flussdichte und $e$ ist die Ladung des Elektrons (auch Elementarladung genannt).
Somit bleiben noch $n$ und $d$ übrig. Die Plattendicke wird mit dem $d$ dargestellt. Du hast sicher schon oft in der Physik (oder auch in Mathematik) den Buchstaben $d$ für eine gegebene oder gesuchte Dicke gesehen.
Das $n$ ist sicherlich neu für dich und steht in diesem Fall für die Elektronendichte.
-
Gib an, welche Aussage auf die Hall-Spannung zutrifft.
TippsHilft dir die Linke-Hand-Regel?
Die Linke-Hand-Regel nutzt du folgendermaßen:
Der Daumen zeigt die Richtung des Stroms (und zwar von - nach +) an und stellt die Ursache dar. Der Zeigefinger gibt die Richtung des magnetischen Feldes an. Der Mittelfinger zeigt dann in die Richtung der Kraft (die Wirkung).
LösungUm die Aufgabe lösen zu können, solltest du die Linke-Hand-Regel (LHR) nutzen. Diese hilft dir herauszufinden, in welche Richtung die Lorentzkraft wirkt. Und da die Bewegung auf Grundlage des Hall-Effekts der Lorentzkraft genau entgegenwirkt, ist die LHR hier hilfreich.
Zur Erinnerung: die LHR nutzt du wie folgt: Der Daumen zeigt die Richtung des Stroms (und zwar von - nach +) an und stellt die Ursache dar. Der Zeigefinger gibt die Richtung des magnetischen Feldes an. Der Mittelfinger zeigt dann in die Richtung der Kraft (die Wirkung). Die Richtung der Wirkung (also des Zeigefingers ist jedoch umzudrehen. Doch an deiner Hand erkennst du sicherlich, dass, egal wohin du sie drehst, alle drei Finger senkrecht aufeinander stehen.
Stellst du dir beispielsweise deine Finger als Kanten eines Würfels vor, so wäre ein Finger die Höhe, einer die Breite und der dritte Finger die Tiefe.
-
Gib die Hall-Spannung zu folgenden gegebenen Werten an: $I= 6,3~A$, $B=1,2~T$, $n=6\cdot10^{25}~m^{-3} $, $d=0,05~mm $.
TippsSchreibe dir die gegebenen und gesuchten Größen auf.
$U_H=\frac{I \cdot B}{n \cdot d \cdot e}$
Hast du das Ergebnis richtig gerundet?
LösungUm diese Aufgabe lösen zu können, schreiben wir zuerst die gegeben und gesuchten Größen auf, halten die Formel zur Berechnung fest, setzen die Zahlenwerte ein und formulieren einen Antwortsatz.
Gegeben: $I= 6,3~A$; $B=1,2~T$; $n=6\cdot10^{25}~m^{-3} $; $d=0,05~mm $
Gesucht: $U_H$ in $mV$
Formel: $U_H=\frac{I \cdot B}{n \cdot d \cdot e}$
Berechnung:
$\begin{align} U_H & =\frac{I \cdot B}{n \cdot d \cdot e} \\ & =\frac{6,3~A \cdot 1,2~T}{6\cdot10^{25}~m^{-3} \cdot 0,00005m \cdot 1,602\cdot 10^{-19}~As} \\ & =0,0157 \frac{A\cdot T}{m^{-3} \cdot m\cdot A\cdot s}=0,0157 \frac{T\cdot m^2}{s} \\ & =0,0157\frac{V\cdot s \cdot m^2}{s \cdot m^2}=0,0157~V=15,7~mV \end{align}$
Antwortsatz: Die Hall-Spannung beträgt $15,7 ~mV$.
9.819
sofaheld-Level
6.600
vorgefertigte
Vokabeln
7.800
Lernvideos
37.183
Übungen
32.618
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Schulstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Physik
- Temperatur
- Schallgeschwindigkeit
- Dichte
- Drehmoment
- Transistor
- Lichtgeschwindigkeit
- Elektrische Schaltungen – Übungen
- Galileo Galilei
- Rollen- Und Flaschenzüge Physik
- Radioaktivität
- Aufgaben zur Durchschnittsgeschwindigkeit
- Lorentzkraft
- Beschleunigung
- Gravitation
- Ebbe und Flut
- Hookesches Gesetz Und Federkraft
- Elektrische Stromstärke
- Elektrischer Strom Wirkung
- Reihenschaltung
- Ohmsches Gesetz
- Freier Fall
- Kernkraftwerk
- Reflexionsgesetz: Ebener Spiegel – Übungen
- Was sind Atome
- Aggregatzustände
- Infrarot, Uv-Strahlung, Infrarot Uv Unterschied
- Isotope, Nuklide, Kernkräfte
- Transformator
- Lichtjahr
- Si-Einheiten
- Fata Morgana
- Gammastrahlung, Alphastrahlung, Betastrahlung
- Kohärenz Physik
- Mechanische Arbeit
- Schall
- Elektrische Leistung
- Dichte Luft
- Ottomotor Aufbau
- Kernfusion
- Trägheitsmoment
- Heliozentrisches Weltbild
- Energieerhaltungssatz Fadenpendel
- Linsen Physik
- Ortsfaktor
- Interferenz
- Diode und Photodiode
- Wärmeströmung (Konvektion)
- Schwarzes Loch
- Frequenz Wellenlänge
- Elektrische Energie


 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?



















Vielen Dank. :)
Hat mir wirklich sehr geholfen für meine Stegreifaufgabe morgen. :)
@Darja*: Das Video müsste funktionieren. Wenn du weiterhin Probleme hast das Video abzuspielen kann dir vielleicht unser Support helfen.
wieso läuft hier kein video?!
Hallo ich bin es noch einmal, ich muss meine Aussage von gerade eben noch einmal zurücknehmen. Ich habe voreilig gepostet. Die Lorenzkraft stimmt. Was den Rest meines Kommentars angeht: einfach nicht beachten.
Hallo, eig. gutes Video. Es haben sich leider nur ein paar Fehler eingeschlichen. Bei ca. 2,02min erklärst du, dass die Technische Stromrichtung von "unten" nach "oben" ist. Nach der Rechten-Hand-Regel müsste die Lorenzkraft dann aber nach links zeigen. Außerdem ist die Richtung der Elektrischen Feldstärke E von plus nach minus und nicht umgekehrt. Bitte ändern. Grüßle.