Zeigerformalismus und Geschichte der Wellenoptik
Beugung und Interferenz von Licht; Interferenz von Licht am optischen Gitter; Kohärenz; Reflexion und Brechung; Aufgaben zur Interferenz von Licht
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
Geschichte der Wellenoptik
Die Geschichte der Wellenoptik beginnt bereits im 15. Jahrhundert. Francesco Grimaldi stellte damals fest, dass sich Licht nicht einfach nur strahlenförmig ausbreiten kann. Er dunkelte damals sein Arbeitszimmer komplett ab und ließ nur durch ein kleines Loch Licht hinein. Als er mit dem Lichtkegel experimentierte, erkannte er, dass die Schatten, die die Körper in diesem Kegel warfen, deutlich größer waren, als er erwartet hatte. Doch seinen Erkenntnissen wurde keine große Beachtung geschenkt.
1664 schlug Robert Hooke vor, dass man sich Licht als Welle vorstellen könne. Auf diesem Wege könnte man sich viele Phänomene erklären. 1690 vertrat Christiaan Huygens, dass sich Licht als Impuls in einem Medium ausbreitet. Auch die Experimente von Thomas Young wie das berühmte Doppelspaltexperiment stützen diese Idee.
Doch die Ideen von Huygens und Young fanden zunächst keine Beachtung, da man die Korpuskel-Theorie von Isaac Newton als richtig erachtete und sich die Theorien zu widersprechen schienen. Nach dieser Theorie bestand das Licht aus kleinsten Körperchen. Da sich aber dennoch viele Phänomene nicht mit der Korpuskel-Theorie erklären ließen, wurde auch ohne Anerkennung an der Wellentheorie des Lichtes gearbeitet. Diese hat bis heute ihre Gültigkeit.
Was ist der Zeigerformalismus?
Der Zeigerformalismus ist ein Hilfsmittel, um z.B. bei Interferenzbildern die Intensität an beliebigen Punkten auf dem Schirm zu berechnen. Dafür bedient man sich der Vektoraddition. Diese kennst du auch schon von der Kräfteaddition. Zur Bestimmung der Intensität zeichnet man zunächst eine Vielzahl von möglichen Lichtwegen von der Lichtquelle durch die Spaltöffnung zum beliebigen Punkt. Diese sollten möglichst gleichmäßig verteilt werden.
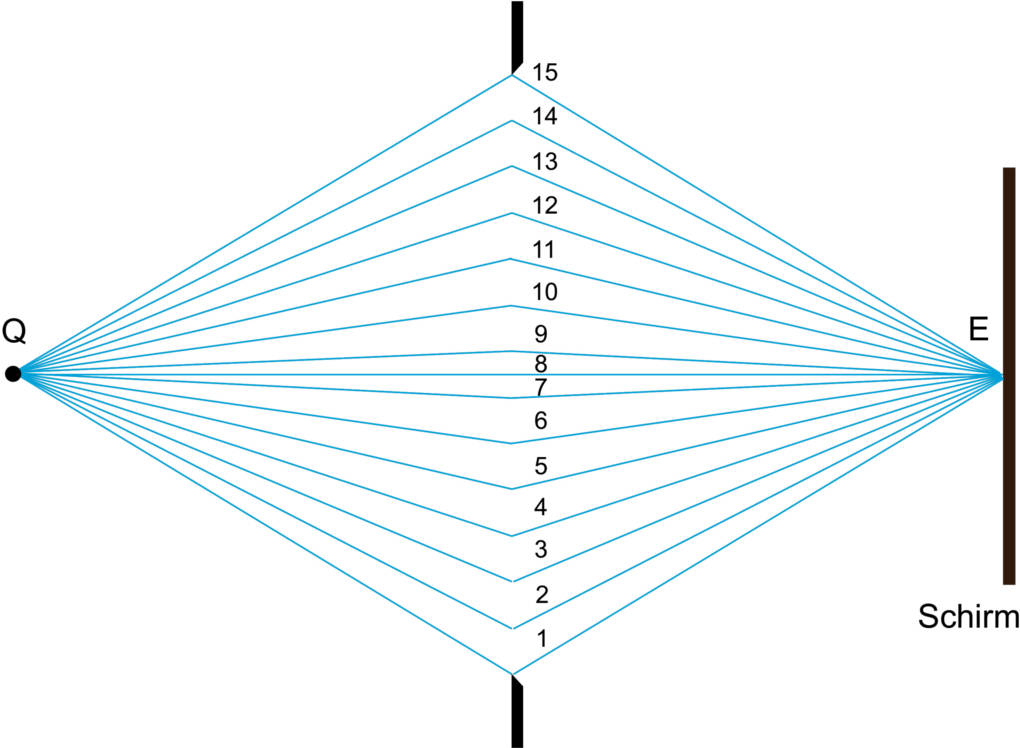
Jedem dieser Lichtwege wird nun ein jeweils gleich langer Zeiger (Vektor) zugeordnet. Begonnen wird mit dem kürzesten Lichtweg. Diesem wird in der Regel die Zeigerstellung 3 Uhr zugeordnet. In diesem Bild ist es der 8. Lichtweg. Eine volle 360°-Drehung des Zeigers steht in diesem Modell für einen Gangunterschied des Lichtes um genau eine Wellenlänge $\lambda$. Nun wird jeweils die Verlängerung des Lichtweges (Gangunterschied) gemessen und ein gleich langer Zeiger mit der entsprechenden Uhrzeit notiert. Dieser Schritt wird auch für alle weiteren Lichtwege ausgeführt.
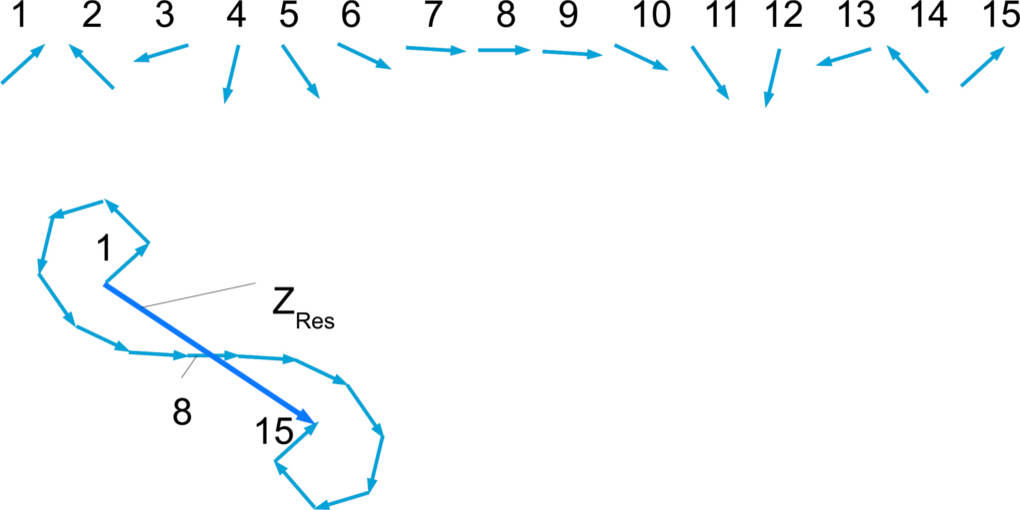
Im Anschluss setzt du dann alle Zeiger zu einem Bild zusammen. Dabei werden in diesem Modell formal alle Zeiger der Lichtwege oberhalb des kürzesten Lichtweges an die Spitze gesetzt und alle unterhalb mit ihrer Spitze ans Ende des Zeigers. Im Abschluss zeichnet man noch den resultierenden Pfeil vom Ende an die Spitze der Pfeilkette. Die Länge dieses Pfeils steht nun für das Verhältnis der Intensität an diesem Punkt zu jedem anderen Punkt auf dem Schirm. Je mehr Lichtwege man verwendet, desto genauer wird das Ergebnis.
Dies kann man nun für jeden beliebigen Punkt auf dem Schirm wiederholen. Da das Verfahren sehr aufwendig ist, verwendet man heute häufig Computer zur Auswertung. Das Ergebnis ist eine Karte der Intensitätsverhältnisse auf dem Schirm. Dort können dann sehr einfach die Minima und Maxima abgelesen werden.
Alle Videos und Lerntexte zum Thema
Videos und Lerntexte zum Thema
Zeigerformalismus und Geschichte der Wellenoptik (6 Videos, 2 Lerntexte)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Zeigerformalismus und Geschichte der Wellenoptik (3 Arbeitsblätter)
Beliebteste Themen in Physik
- Temperatur
- Schallgeschwindigkeit
- Dichte
- Drehmoment
- Transistor
- Lichtgeschwindigkeit
- Elektrische Schaltungen – Übungen
- Galileo Galilei
- Rollen- Und Flaschenzüge Physik
- Radioaktivität
- Aufgaben zur Durchschnittsgeschwindigkeit
- Lorentzkraft
- Beschleunigung
- Gravitation
- Ebbe und Flut
- Hookesches Gesetz Und Federkraft
- Elektrische Stromstärke
- Elektrischer Strom Wirkung
- Reihenschaltung
- Ohmsches Gesetz
- Freier Fall
- Kernkraftwerk
- Reflexionsgesetz: Ebener Spiegel – Übungen
- Was sind Atome
- Aggregatzustände
- Infrarot, Uv-Strahlung, Infrarot Uv Unterschied
- Isotope, Nuklide, Kernkräfte
- Transformator
- Lichtjahr
- Si-Einheiten
- Fata Morgana
- Gammastrahlung, Alphastrahlung, Betastrahlung
- Kohärenz Physik
- Mechanische Arbeit
- Schall
- Elektrische Leistung
- Dichte Luft
- Ottomotor Aufbau
- Kernfusion
- Trägheitsmoment
- Heliozentrisches Weltbild
- Energieerhaltungssatz Fadenpendel
- Linsen Physik
- Ortsfaktor
- Interferenz
- Diode und Photodiode
- Wärmeströmung (Konvektion)
- Schwarzes Loch
- Frequenz Wellenlänge
- Elektrische Energie










 Intensität von Licht – Zeigerformalismus und Interferenz
Intensität von Licht – Zeigerformalismus und Interferenz
 Zeigerformalismus
Zeigerformalismus
 Wellenoptik – elektromagnetisches Spektrum
Wellenoptik – elektromagnetisches Spektrum









