Linsen und Abbildungsgeräte
Linsen sind in der Lage das Licht zu bündeln oder auch zu zerstreuen. Sie werden häufig verwendet.
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Linsen und Abbildungsgeräte in Alltag und Beruf
- Linsenformen – konvex und konkav
- Bildentstehung an Linsen
- Linsengleichung und Abbildungsgesetz
- Abbildungsgeräte
Linsen und Abbildungsgeräte in Alltag und Beruf
Im Alltag und Beruf werden viele Linsen und Abbildungsgeräte verwendet, seien dies nun Lupen, Ferngläser, Visiere, Teleskope oder Fernrohre, Brillen, Monokel, Mikroskope, Beamer, Tageslichtprojektoren, Diaprojektoren, Periskope, Fotoapparate oder jede andere Form der Kamera. In diesen Geräten finden sich zumeist Linsen, aber auch gekrümmte Spiegel.
Linsenformen – konvex und konkav
Alle Linsen haben gemeinsam, dass sie lichtdurchlässige Körper sind. Diese besondere Art der lichtdurchlässigen Körper kann zwei Formen annehmen. Eine davon ist die konvexe Form. Diese ist in der Mitte viel dicker als am Rand und sammelt das Licht in einem besonderen Punkt: dem Brennpunkt. Daher nennt man Linsen dieser Form auch Sammellinsen.
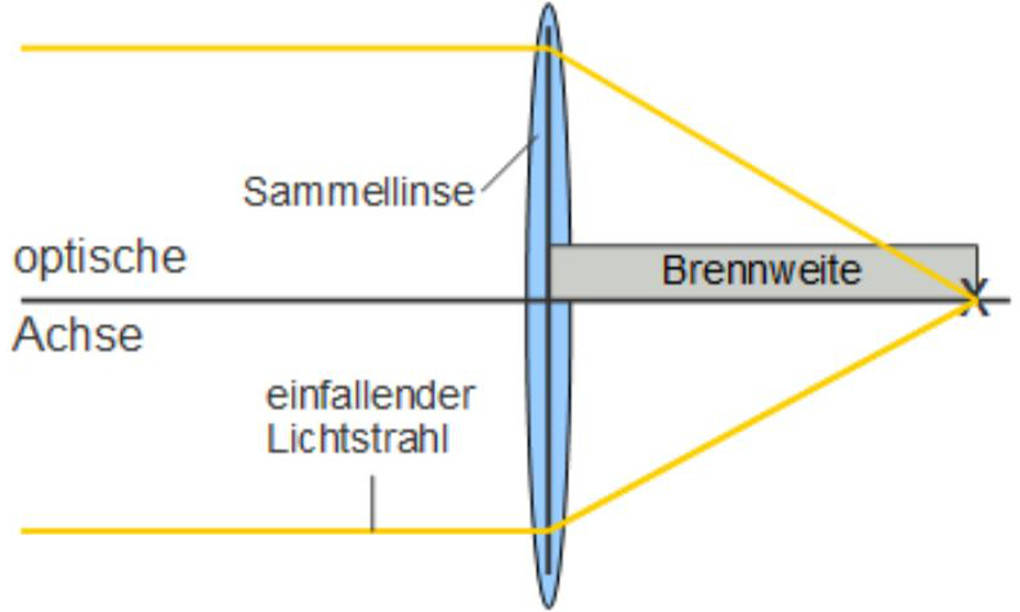
Die konkave Form ist die zweite Form der Linsen in Physik. Diese ist in der Mitte viel dünner als am Rand und zerstreut das Licht aus einem gemeinsamen Brennpunkt. Daher nennt man Linsen dieser Form auch Zerstreuungslinsen.
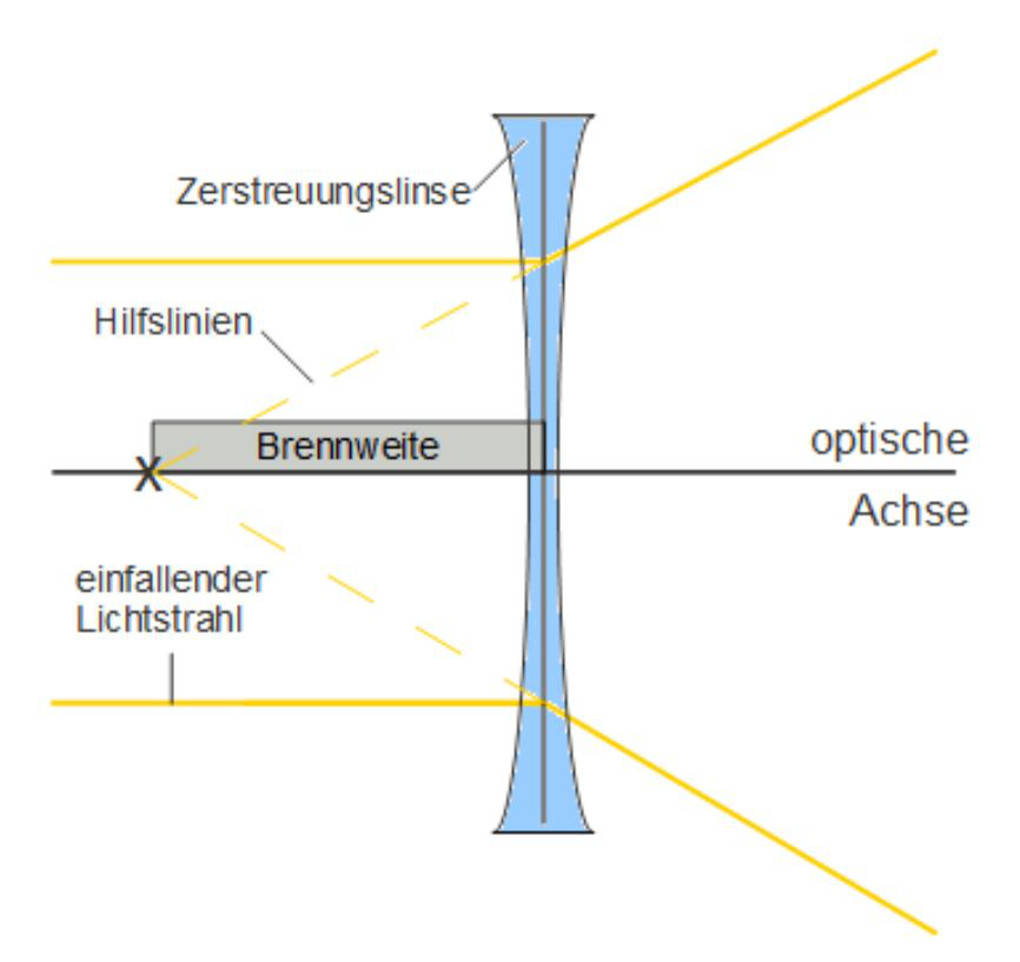
Linsen lassen sich durch zwei Größen beschreiben: durch ihren Durchmesser und durch die Brennweite. Die Brennweite ist die Entfernung vom Mittelpunkt der Linse bis zum Brennpunkt in Millimeter $\text{mm}$. Dieser Wert ist für eine Sammellinse positiv, da ihr Brennpunkt für das Licht immer hinter der Linse liegt, und für eine Zerstreuungslinse immer negativ, da der Brennpunkt für das Licht immer vor der Linse liegt. Eine Zerstreuungslinse und eine Sammellinse, deren Brennweiten denselben Betrag besitzen, würden ihre Wirkungen genau aufheben.
Bildentstehung an Linsen
Die beiden Linsenformen erzeugen unterschiedliche Abbilder. Diese lassen sich mit Hilfe von drei Hilfsstrahlen optisch konstruieren. Dazu zeichnet man zunächst vom Gegenstandspunkt G aus einen Strahl parallel zur optischen Achse bis zur Linsenebene. Dieser Strahl ist der Parallelstrahl. Der Parallelstrahl wird ab der Linsenebene zum Brennpunktstrahl, geht durch den Brennpunkt der Linse und wird darüber hinaus noch verlängert. Dann zeichnet man einen dritten Strahl: den Mittelpunktstrahl. Dieser geht vom Gegenstandspunkt G aus durch den Schnittpunkt von optischer Achse und Linsenebene und wird darüber hinaus verlängert. Der Mittelpunktstrahl und der Brennpunktstrahl schneiden sich an einem Punkt. Dies ist der Abbildungspunkt A. Dieser Punkt ist die Abbildung des Gegenstandspunktes G. Das Bild an der Sammellinse steht nach dieser Konstruktion auf dem Kopf.
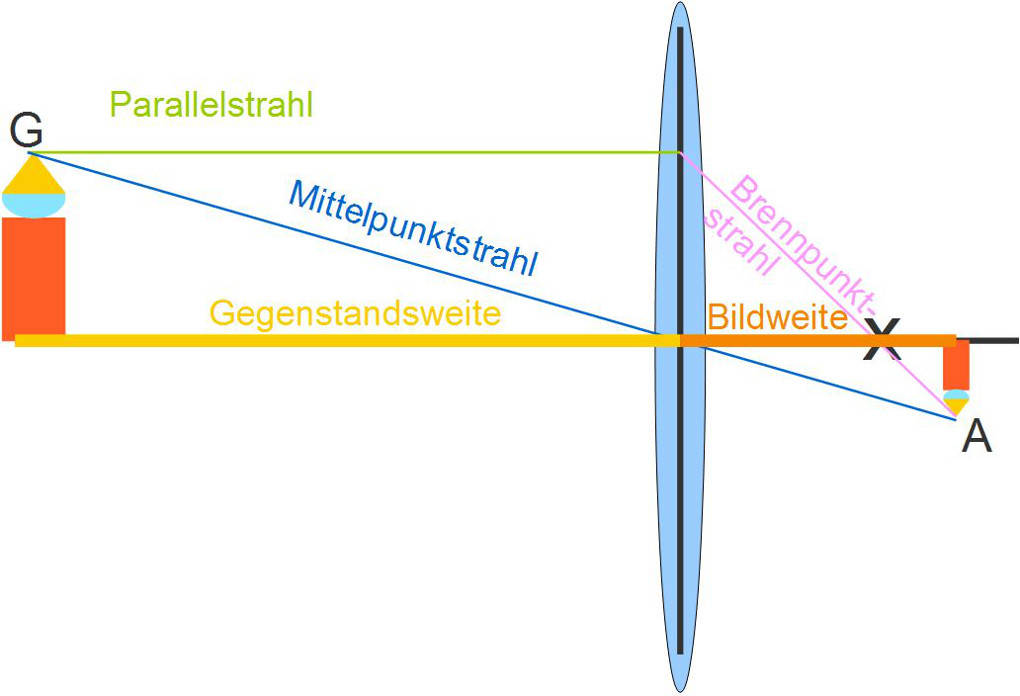
Bei der Konstruktion eines Abbildes mit einer Zerstreuungslinse geht man genauso vor, nur dass hier der Brennpunkt auf derselben Seite liegt wie der Gegenstand. Der Brennpunktstrahl ist daher auch nur eine rückwärts verlängerte Hilfslinie. Am Schnittpunkt vom Mittelpunktstrahl und der Hilfslinie des Brennpunktstrahls finden wir wieder unseren Abbildungspunkt A.
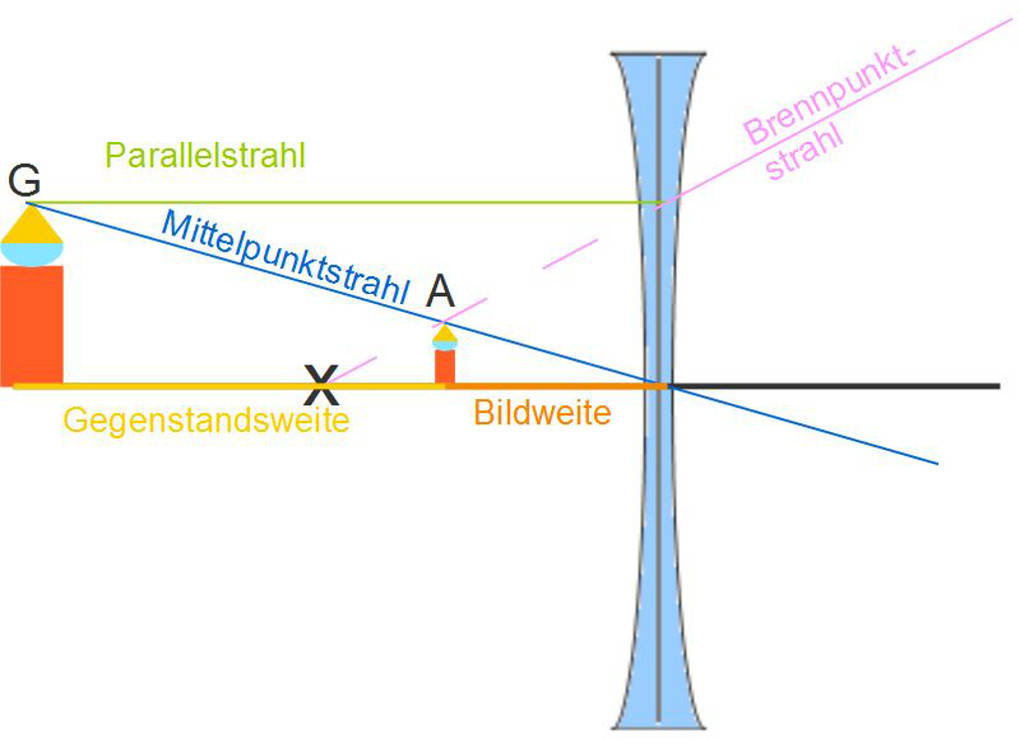
Aus den Zeichnungen können wir auch noch zwei weitere Größen ablesen: die Bildweite $b$ und die Gegenstandsweite $g$.
Linsengleichung und Abbildungsgesetz
Nicht nur mit der optischen Konstruktion, auch auf rechnerischem Wege kann man die Verhältnisse genau ermitteln. Dabei hilft dir die Linsengleichung und das Abbildungsgesetz. Die Linsengleichung gibt an, dass der Kehrwert der Brennweite gleich der Summe der Kehrwerte von Bildweite und Gegenstandsweite ist:
$\frac 1f=\frac 1b + \frac 1g$.
Mit dieser Gleichung kann man über den Abstand des Gegenstandes zur Linsenebene, also der Gegenstandsweite $g$, und dem Abstand des Bildes von der Linsenebene, also der Bildweite $b$, die Brennweite der Linse $f$ und bei bekannter Brennweite $f$ die Position des Gegenstandes oder des Bildes bestimmen. Mit Hilfe dieser Gleichung kann man einen optischen Aufbau sehr leicht konstruieren ohne lange zu probieren. Aber auch das Abbildungsgesetz hilft bei der Konstruktion eines optischen Aufbaus. Mit diesem kann man sehr leicht den Vergrößerungsfaktor $V$, auch Abbildungsverhältnis $A$ genannt, bestimmen. Das Verhältnis von Bildgröße $B$ zur Gegenstandsgröße $G$ gibt den Vergrößerungsfaktor genau an. Es ist aber auch die alternative Bestimmung mit Hilfe der Bild und Gegenstandsweite oder auch der Bildweite und Brennweite möglich.
$A=V=\frac BG=\frac bg =\frac{b-f}{f}$.
Diese Gesetze geben dir die Möglichkeit, auch rechnerisch schnell die richtigen Abstände einzustellen.
Abbildungsgeräte
Mit Ausnahme der Brille, der Lupe und des Monokels bestehen die meisten Abbildungsapparate aus einer Kombination hintereinander gereihter Linsen. Durch eine Mechanik, welche den Linsenabstand verändert, lässt sich die Schärfe des Bildes in Abhängigkeit vom untersuchten Objekt einstellen. Bei all diesen Apparaten gibt es unabhängig von der Form der Linse zwei Benennungen: Objektiv für die Linse, die auf das Objekt gerichtet ist, und Okular, die Linse, durch die wir hindurchschauen. Bei hochwertigen Geräten kann zumeist das Objektiv ausgetauscht werden wie beim Teleobjektiv und dem Weitwinkel einer Spiegelreflexkamera oder bei den unterschiedlichen Objektiven eines Mikroskops. Der Namensgeber der Kamera – was so viel wie „Zimmer” bedeutet – ist ein Abbildungsapparat ohne Linse, die sogenannte Lochkamera.
Alle Videos und Lerntexte zum Thema
Videos und Lerntexte zum Thema
Linsen und Abbildungsgeräte (9 Videos, 2 Lerntexte)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Linsen und Abbildungsgeräte (9 Arbeitsblätter)
Beliebteste Themen in Physik
- Temperatur
- Schallgeschwindigkeit
- Dichte
- Drehmoment
- Transistor
- Lichtgeschwindigkeit
- Elektrische Schaltungen – Übungen
- Galileo Galilei
- Rollen- Und Flaschenzüge Physik
- Radioaktivität
- Aufgaben zur Durchschnittsgeschwindigkeit
- Lorentzkraft
- Beschleunigung
- Gravitation
- Ebbe und Flut
- Hookesches Gesetz Und Federkraft
- Elektrische Stromstärke
- Elektrischer Strom Wirkung
- Reihenschaltung
- Ohmsches Gesetz
- Freier Fall
- Kernkraftwerk
- Reflexionsgesetz: Ebener Spiegel – Übungen
- Was sind Atome
- Aggregatzustände
- Infrarot, Uv-Strahlung, Infrarot Uv Unterschied
- Isotope, Nuklide, Kernkräfte
- Transformator
- Lichtjahr
- Si-Einheiten
- Fata Morgana
- Gammastrahlung, Alphastrahlung, Betastrahlung
- Kohärenz Physik
- Mechanische Arbeit
- Schall
- Elektrische Leistung
- Dichte Luft
- Ottomotor Aufbau
- Kernfusion
- Trägheitsmoment
- Heliozentrisches Weltbild
- Energieerhaltungssatz Fadenpendel
- Linsen Physik
- Ortsfaktor
- Interferenz
- Diode und Photodiode
- Wärmeströmung (Konvektion)
- Schwarzes Loch
- Frequenz Wellenlänge
- Elektrische Energie














 Wie funktioniert eine Lochkamera?
Wie funktioniert eine Lochkamera?
 Linsen
Linsen
 Optische Abbildungen
Optische Abbildungen
 Die Linsengleichung
Die Linsengleichung
 Fernrohre
Fernrohre
 Lupe und Mikroskop
Lupe und Mikroskop
 Lichtleiter
Lichtleiter
 Fotografie
Fotografie
 Lochkamera
Lochkamera









