Beschleunigte Bewegungen
Beschleunigung; Gleichmäßig beschleunigte und gleichmäßig verzögerte Bewegung
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Überblick über die Formen der Bewegung
- Die Beschleunigung
- Die Bremsbewegung
- Darstellung von Bewegungen im Diagramm
Überblick über die Formen der Bewegung
Ein Körper, der seinen Ort verändert, ist in Bewegung. Die Bewegungsarten können sehr unterschiedlich sein. Man unterscheidet hier zwei Eigenschaften der Bewegung: die Richtung und den zeitlichen Verlauf. Die Richtung der Bewegung kann geradlinig sein, also immer in dieselbe Richtung erfolgen, kreisförmig sein, also immer um den selben Wert zur gleichen Seite abgelenkt werden, ellipsenförmig, so wie die Planetenbewegungen um die Sonne, oder auch komplett willkürlich. Genauso lässt sich auch der zeitliche Verlauf der Bewegung unterscheiden: Die Bewegung kann gleichförmig sein, das bedeutet, dass sich der Ort des Körpers in einem gleich großen Zeitfenster auch immer gleich stark verändert. Die Bewegung kann aber auch gleichmäßig beschleunigt sein, das bedeutet, dass sich die Geschwindigkeit immer um denselben Wert verändert. Zuletzt kann sie auch einfach nur beschleunigt sein. Hier ändert sich die Geschwindigkeit des Körpers willkürlich.
Die Beschleunigung
Jede Bewegung kann durch drei Größen beschrieben werden, die immer von der Zeit abhängig sind: Der Ort $S$ zum Zeitpunkt $T$, welcher durch die Strecke oder den Weg $s$ beschrieben wird, die Streckenveränderung $\Delta s$ über die Zeitdauer $\Delta t$, welche durch die Geschwindigkeit $v$ beschrieben wird, und die Geschwindigkeitsänderung $\Delta v$ über die Zeitdauer $\Delta t$, welche über die Beschleunigung $a$ beschrieben wird. Damit lässt sich jede Bewegung mit den Größen Weg, Geschwindigkeit und Beschleunigung darstellen.
$\text{Weg }s=s_0 + v \cdot t + \frac12 \cdot a \cdot t^2$ , $[s] = \text{m}$
$\text{Geschwindigkeit }v=v_0 + a \cdot t$ , $[v] = \frac{\text{m}}{\text{s}}$
$\text{Beschleunigung }a=\frac{\Delta v}{\Delta t}$ , $[a] = \frac{\text{m}}{\text{s}^2}$
Selbst komplizierte beschleunigte Bewegungen wie der Flug einer dreistufigen Rakete lassen sich über diese drei Größen darstellen. Die Strecke würde über den Verlauf der Flugkurve immer weiter ansteigen, während die Geschwindigkeit beim Starten der Stufen stark zunehmen würde, um dazwischen durch die Reibung wiederum reduziert zu werden. Die Beschleunigung wäre zu den drei Zeitpunkten sehr groß und dazwischen negativ.
Die Bremsbewegung
Bei der Verkehrserziehung ist aus der Sicherheitperspektive eines sehr wichtig: das Bremsen.
Bei dieser gleichmäßig verzögerten Bewegung sind unterschiedliche Größen wichtig: zum einen die Bremsbeschleunigung $a_B$, die stets negativ ist. Diese ist durch das vorliegende Material beim Bremsvorgang bestimmt, also den Zustand der Bremsen, die Haftung auf dem Untergrund usw. Durch diese Beschleunigung wird die Geschwindigkeit bei einer Vollbremsung gleichmäßig reduziert. Auch die Ausgangsgeschwindigkeit $v_0$ ist für den Bremsweg von zentraler Bedeutung. Am häufigsten berechnet wird aus diesen Werten der Bremsweg $s_b$. Für die Berechnung des Bremsweges gilt folgende Gleichung:
$s_B(t)=\frac{1}{2}\cdot a_B \cdot t_B^2 + v_0 \cdot t_B + s_0$.
Für den Anhalteweg ist auch die sogenannte Schrecksekunde von Bedeutung. Dies ist die Zeit, die vergeht, bis bei einer Gefährdung die Bremsen voll betätigt werden können. Diese Schrecksekunde wird besonders durch die Einnahme von Rauschmitteln erhöht. Während dieser Schrecksekunde wird mit der Ausgangsgeschwindigkeit $v_0$ ungebremst weitergefahren. Laut Fahrschule gilt für einen nicht beeinträchtigten Fahrer ein Reaktionsweg $s_R$ von:
$s_R=\frac{v_0}{10}\cdot 3$.
Der Anhalteweg $s_A$ ist die Summe von Bremsweg $s_B$ und Reaktionsweg $s_R$:
$s_A=s_B + s_R$.
Darstellung von Bewegungen im Diagramm
Aus dem vorherigen Unterricht kennst du bereits das t-s-Diagramm oder auch Zeit-Weg-Diagramm. In diesem wird die zurückgelegte Strecke $s$ über die Zeit $t$ aufgetragen. Die jeweilige Steigung in diesem Graphen entspricht der Geschwindigkeit $v$ zum jeweiligen Zeitpunkt $T$. Auch das t-v-Diagramm oder auch Zeit-Geschwindigkeit-Diagramm ist dir bekannt. In diesem wird die Geschwindigkeit $v$ über die Zeit $t$ aufgetragen. Die Steigung dieses Graphen entspricht der Beschleunigung $a$. Stellen wir eine beschleunigte Bewegung in den unterschiedlichen Diagrammen dar:
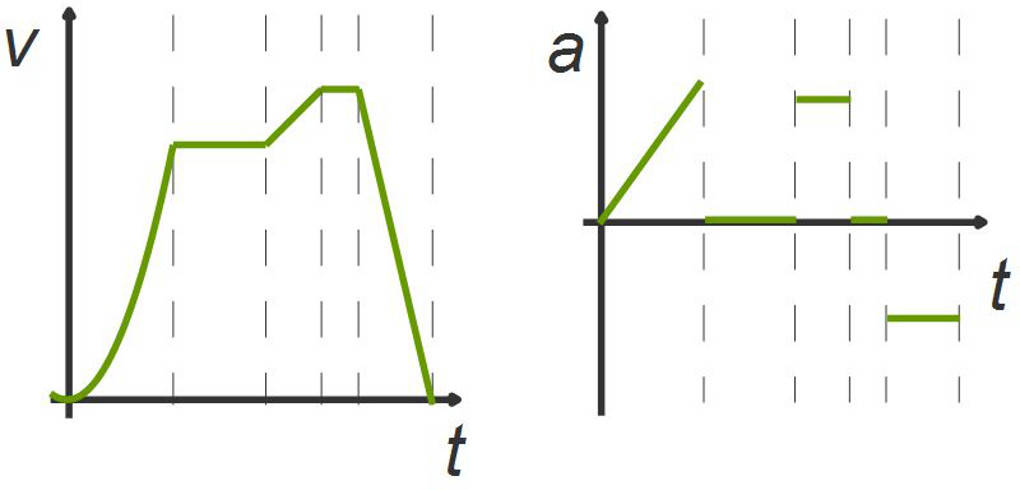
Vergleicht man diese Graphen, stellt man fest, dass sie die gleiche Bewegung zeigen.
Alle Videos und Lerntexte zum Thema
Videos und Lerntexte zum Thema
Beschleunigte Bewegungen (4 Videos, 2 Lerntexte)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Beschleunigte Bewegungen (6 Arbeitsblätter)
-
 Gleichmäßig beschleunigte Bewegung
PDF anzeigen
Gleichmäßig beschleunigte Bewegung
PDF anzeigen -
 Freier Fall als beschleunigte Bewegung
PDF anzeigen
Freier Fall als beschleunigte Bewegung
PDF anzeigen -
 Beschleunigte Bewegung – Darstellung im Diagramm
PDF anzeigen
Beschleunigte Bewegung – Darstellung im Diagramm
PDF anzeigen -
 Bremsvorgang – gleichmäßig verzögerte Bewegung
PDF anzeigen
Bremsvorgang – gleichmäßig verzögerte Bewegung
PDF anzeigen -
 Endgeschwindigkeit und Luftwiderstand
PDF anzeigen
Endgeschwindigkeit und Luftwiderstand
PDF anzeigen -
 Rechnen mit geradlinig gleichförmigen und gleichmäßig beschleunigten Bewegungen
PDF anzeigen
Rechnen mit geradlinig gleichförmigen und gleichmäßig beschleunigten Bewegungen
PDF anzeigen
Beliebteste Themen in Physik
- Temperatur
- Schallgeschwindigkeit
- Dichte
- Drehmoment
- Transistor
- Lichtgeschwindigkeit
- Elektrische Schaltungen – Übungen
- Galileo Galilei
- Rollen- Und Flaschenzüge Physik
- Radioaktivität
- Aufgaben zur Durchschnittsgeschwindigkeit
- Lorentzkraft
- Beschleunigung
- Gravitation
- Ebbe und Flut
- Hookesches Gesetz Und Federkraft
- Elektrische Stromstärke
- Elektrischer Strom Wirkung
- Reihenschaltung
- Ohmsches Gesetz
- Freier Fall
- Kernkraftwerk
- Reflexionsgesetz: Ebener Spiegel – Übungen
- Was sind Atome
- Aggregatzustände
- Infrarot, Uv-Strahlung, Infrarot Uv Unterschied
- Isotope, Nuklide, Kernkräfte
- Transformator
- Lichtjahr
- Si-Einheiten
- Fata Morgana
- Gammastrahlung, Alphastrahlung, Betastrahlung
- Kohärenz Physik
- Mechanische Arbeit
- Schall
- Elektrische Leistung
- Dichte Luft
- Ottomotor Aufbau
- Kernfusion
- Trägheitsmoment
- Heliozentrisches Weltbild
- Energieerhaltungssatz Fadenpendel
- Linsen Physik
- Ortsfaktor
- Interferenz
- Diode und Photodiode
- Wärmeströmung (Konvektion)
- Schwarzes Loch
- Frequenz Wellenlänge
- Elektrische Energie


















