Helligkeiten und Entfernungen der Sterne

Hallo, hier ist wieder Dr. Psi. Wir beschäftigen uns heute mit der Helligkeit und der Entfernung von Sternen von der Erde. Dabei begegnen wir unter anderem Begriffen wie Parsek, Parallaxe und Lichtjahr. Beginnen wir also mit dem Erscheinungsbild der Sterne. Blicken wir in den nächtlichen Sternenhimmel, so erscheinen uns einzelne Sterne unterschiedlich hell. Ein physikalisches Maß für den von unserem Auge registrierten Lichteindruck ist die so genannte scheinbare Helligkeit m. Also, die zur Erde gelangte Strahlungsintensität eines Sterns. Als Einheit für m wird von alters her die Größenklasse verwendet. Dazu schrieb man zum Beispiel für die hellsten Sterne 1^m. m war die scheinbare Helligkeit und die schwächsten, gerade noch mit unserem Auge sichtbaren Sterne, mit 6^m. Später erweiterte man die entsprechende Skala dann um negative Werte, natürlich zwischendurch die Null und auch Zwischenwerte. Schauen wir uns einmal einige Beispiele an und zwar in dieser Tabelle, die wir sehen. Dort finden wir auf der einen Seite Himmelskörper und auf der anderen Seite die scheinbare Helligkeit. Diesmal nicht nur mit ganzen Zahlen, sondern auch mit negativen Zahlen und irgendwann wird ein Stern auch mit der scheinbaren Helligkeit null bezeichnet werden. Wir beschränken uns hier nur auf einige Sterne. Schauen wir mal die ersten drei Sterne, also den Sirius, Rigel und Polarstern an. Das sind Fixsterne. Wir haben hier die entsprechende scheinbare Helligkeit und die beiden anderen Einträge. Das sind Planeten Venus und Mars. Diese variieren natürlich, die ändern ihre Intensität durch ihre Bewegung. Die variieren also in ihrer scheinbaren Helligkeit. Gucken wir uns als nächstes etwas näher die Entfernungen der Sterne an. Die scheinbare Helligkeit eines Sterns wird durch seine Leuchtkraft und durch seine Entfernung von der Erde beeinflusst. 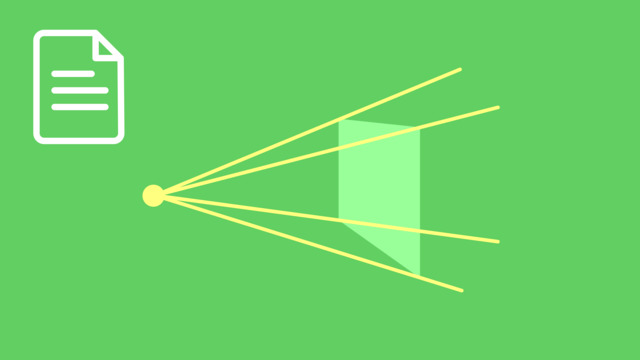Schauen wir uns mal diese Abbildung an. Sie verdeutlicht, dass sich das Licht einer Lichtquelle mit zunehmender Entfernung von dieser Lichtquelle auf eine immer größere Fläche verteilt. Daher erscheint ein Stern in geringerer Entfernung heller, als in weiterer Entfernung. Wie lässt sich nun die Entfernung eines Sterns bestimmen? Direkt abmessen geht ja wohl nicht. Schauen wir uns einmal diese Abbildung an. Die Erde bewegt sich um die Sonne und ändert dadurch die Position und damit ändert sich auch die scheinbare Position eines Sterns am Himmel. Das sehen wir hier auf dieser Abbildung. Die Erde bewegt sich. Der Stern hat eine feste Position und am Himmelszelt gewissermaßen erscheint der Stern an einer anderen Stelle. Nun mit Präzisionsinstrumenten lässt sich das alles genau bestimmen und wir sehen hier den Buchstaben p. Man nennt Winkel, die dadurch entstehen, dass sich ein Beobachter in seinem Standort verändert und sich dabei eine Position eines anderen Objektes scheinbar verändert. Nämlich die Betrachtung des Objektes von der Erde zum Beispiel zu diesem Stern und dieser Winkel, der sich dabei ergibt, oder diese Winkel an sich, nennt man Parallaxen. Die Astronomie hat diesen halben Beobachtungswinkel zwischen den Sehstrahlen von der Position der Erde zu einem Stern als Parallaxe p bezeichnet. Und wir sehen hier auf diesem Bild weiterhin nochmal die Ekliptik, also die Bahn der Erde und in der Mitte sehen wir die Sonne und die Entfernung Sonne zur Erde wird mit R gleich eine astronomische Einheit, abgekürzt AE, bezeichnet. Wir kommen noch einmal darauf zurück. Nun sind die gemessenen Sternparallaxen sehr, sehr klein. Daher benutzt man für diese Parallaxen einmal die Winkelminute. Das ist Eins mit einem kleinen Apostroph und das ist ein Grad geteilt durch 60. Und wir benützen auch noch die Winkelsekunde. Das ist ein Grad geteilt durch 3600. Und diese Größen werden hier mit Präzisionsinstrumenten gemessen und daraus kann der Astronom Rückschlüsse auf die Entfernung ziehen. So, das waren nun ein paar Details. Wir machen eine kleine Unterbrechung und sehen uns gleich in der nächsten Szene etwas mehr zur Entfernungsbestimmung der Sterne an. Wir hatten gerade über die Sternparallaxen geredet und, dass diese recht klein sind. Beachten wir nun, dass ein Stern, wir sehen das in dieser Abbildung hier, mit einer Parallaxe von einer Winkelsekunde, einen Abstand von der Erde von rund 200.000 astronomischen Einheiten hat. So leuchtet es fast ein, dass wir eine neue Entfernungseinheit benötigen. Die neue Entfernungseinheit leitet sich ab von dem Begriff Parallaxensekunde und diese Parallaxensekunde wird auch gerne geschrieben als Parsec oder das Symbol pc. Und es gilt: 1pc = 3,086 * 10¹³km. Das hat man so festgelegt. Und wenn wir uns mal in dieser Bildung vertiefen, so sehen wir dort einen Stern, der wurde beobachtet unter der Parallaxensekunde, also in diesem Fall mit einem pc und er hat also eine Entfernung von der Erde von 3,086 mal zehn hoch dreizehn Kilometer. Es gibt aber noch eine andere Entfernungseinheit. Das ist das Lichtjahr und das Lichtjahr wird gelegentlich abgekürzt mit Lj. Manchmal finden wir auch Ly. Nun, wie schon der Begriff “Lichtjahr” aussagt, ist diese Entfernungseinheit so zu verstehen, dass das Licht im Vakuum liegt, in einem Jahr eine bestimmte Strecke zurücklegt und genau das bezeichnet man als ein Lichtjahr. Und es ist dann festgelegt: 1Lj = 9,5 * 10¹²km. Und damit kann man auch diese beiden Größen hier miteinander verbinden, so dass wir schreiben könnem: 1pc = 3,26 Lj. Ja, das sind wieder ein paar Einheiten zum Angeben von Entfernungen der Sterne von der Erde. Und nun wollen wir uns in einer nächsten Szene noch etwas über die Bestimmung der absoluten Helligkeit von Sternen ansehen. Ja, wir hatten festgestellt, dass die Helligkeit der Sterne von der Entfernung der Sterne zur Erde und ihrer Leuchtkraft abhängig ist. Um dies, diese beiden Abhängigkeiten, zu umgehen, also, damit die Helligkeit der Sterne unabhängig von diesen Größen miteinander vergleichbar ist, hat man sich etwas ausgedacht. Man hat in der Astrophysik die absolute Helligkeit M eingeführt und damit wird die Helligkeit bezeichnet, mit der ein Stern aus einer Entfernung von 10pc zu beobachten ist. Und mit der Helligkeit, mit der er dort erscheint, das ist ein Maß für die Leuchtkraft der Sterne. Gucken wir uns das mal in dieser Abbildung an. Um einen Wert von M, die absolute Helligkeit, anzugeben, wird ein Stern gedanklich so verschoben, dass er in einer Entfernung von zehn Parsec versetzt wird. Ist er tatsächlich weiter, erscheint er natürlich dann näher an der Erde und wird gedanklich heller und, umgekehrt natürlich, wird er gedanklich dunkler, wenn er aus einer näheren Entfernung nach zehn Parsec verschoben wird. Und so ist es möglich, mit Hilfe von bestimmten Gesetzen, wir haben ja am Anfang gesehen, Entfernung und Fläche, mit diesen Gesetzen eine absolute Helligkeit von Sternen anzugeben. Ja, damit sind wir schon am Ende. Wir fassen jetzt kurz zusammen, was wir heute gelernt haben. Wir haben uns heute mit der Entfernung und der Helligkeit von Sternen beschäftigt und haben einige Methoden kennengelernt, mit denen man die Helligkeiten und die Entfernung bestimmen kann. Außerdem haben wir Begriffe wie Parallaxe, Parsec und Lichtjahr kennengelernt. Die Helligkeit selbst haben wir in scheinbare und absolute Helligkeit eingeteilt. Soweit die Erklärungen zur absoluten Helligkeit, die in der Schulphysik oft verwendet wird. Die Fachwissenschaft benutzt zur Beschreibung der Helligkeit von Sternen zusätzlich den Begriff der bolometrischen Helligkeit. Für den Fall, dass Du Dich darüber genauer informieren willst, kannst Du im Internet entsprechend recherchieren.