Thermische Energie

Inhaltsverzeichnis zum Thema

• Teilchenmodell
• Innere Energie
• Wärme und thermische Energie
  • Beispiel:

Teilchenmodell

Um verschiedene physikalische Vorgänge begreifen zu können, entwickelten die Wissenschaftler das sogenannte Teilchenmodell der Materie. Die Modellvorstellung kommt der Wirklichkeit sehr nahe und stützt sich auf drei Aussagen:

Alle Stoffe bestehen aus vielen kleinsten Teilchen, sie sind aus Atomen aufgebaut. Egal ob du Luft, Wasser oder einen festen Körper betrachtest, seine Teilchen kannst du selbst unter einer Lupe nicht erkennen.

Zwischen den Teilchen wirken Kräfte. Dadurch ziehen sich die einzelnen Teilchen gegenseitig an oder stoßen sich ab. Je näher sich die Teilchen sind, desto stärker wirken die Kräfte – wie bei Magneten.

Die Teilchen sind dadurch in ständiger Bewegung. Diese ruckartigen, unregelmäßigen Bewegungen werden als brownsche Bewegung bezeichnet. Je höher die Temperatur der Materie ist, desto stärker ist diese.

Innere Energie

Jeder feste, flüssige oder gasförmige Körper hat innere Energie gespeichert. Sie ist die Summe aus drei verschiedenen Energiearten.

• Bindungsenergie: $E_{bind}$
• Kernphysikalische Energie: $E_{kern}$
• Thermische Energie: $E_{therm}$

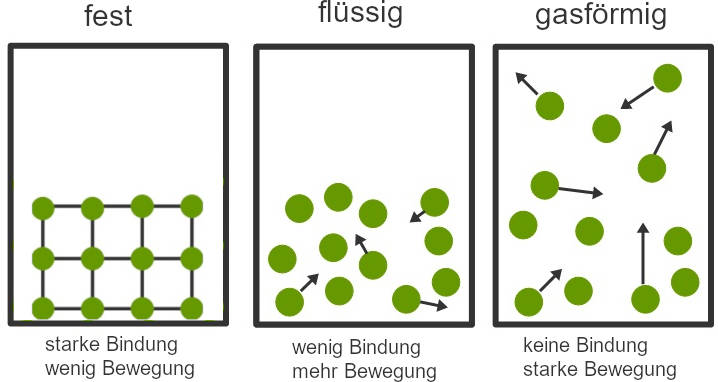
Je näher sich die Teilchen sind, desto stärker wirken die Bindungskräfte. In festen Stoffen sind sich die Teilchen sehr nahe, bei Flüssigkeiten schon weniger nahe und bei Gasen können sie sich fast frei bewegen. Daher ist die Bindungsenergie in Festkörpern am höchsten.

Die kernphysikalische Energie ist in den Atomkernen gespeichert. Sie wird frei, wenn das Atom z. B. gespalten wird (Atomkraft) oder radioaktiv zerfällt. Diese Energieform hat der Menschheit schon viel Nutzen und viel Leid gebracht. Daher wird immer wieder darüber diskutiert, das ein oder andere Kernkraftwerk abzuschalten.

Jedes Teilchen bewegt sich und besitzt dadurch Bewegungsenergie. Die durchschnittliche Bewegungsenergie aller Teilchen eines Stoffes wird als thermische Energie bezeichnet. Diese Wärmeenergie steigt an, wenn der Stoff erwärmt wird und verringert sich beim Abkühlen. Bei der absoluten Temperatur $0$ Kelvin stehen alle Teilchen still. Daher ist die thermische Energie dort null.

Wärme und thermische Energie

Zugeführte Wärme $Q$ kann in Form von thermischer Energie gespeichert werden oder den Aggregatzustand eines Stoffes ändern. Die Wärmemenge $Q$, die als thermische Energie gespeichert wird, lässt sich mit dem Erwärmungsgesetz berechnen:

$ Q = c\cdot m\cdot \Delta T $

Dabei ist $m$ die Masse, $\Delta T$ der Temperaturunterschied und $c$ die spezifische Wärmekapazität, die vom Material abhängt.

Beispiel:

Ein Eisenstück mit der Masse $m=3 kg$ soll von $8^\circ C$ auf $10^\circ C$ erwärmt werden. Wie viel Wärme $Q$ muss dafür zugeführt werden?

Die spezifische Wärmekapazität von Eisen kannst du im Physikbuch oder im Internet nachlesen. Sie beträgt $c= 0,460 \frac{KJ}{kg\cdot K}$. Das bedeutet, dass $0,46 J$ an Wärme nötig sind, um ein Kilogramm Eisen um ein Kelvin (oder auch Grad Celsius) zu erwärmen.

$ m = 3 kg\\ Q = c \cdot m \cdot \Delta T\\ Q = 0,460 \frac{KJ}{kg\cdot K}\cdot 3 kg \cdot (10^\circ C - 8^\circ C) = 2,76 KJ = 2760 J $

Es sind also insgesamt $2760 J$ an Wärmemenge nötig, um das Eisenstück um $2^\circ C$ zu erwärmen.