Elektronenbeugung am Doppelspalt


in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Grundlagen zum Thema Elektronenbeugung am Doppelspalt
In diesem Video geht es um die Beugung von Elektronenstrahlen am Doppelspalt. Denn obwohl Elektronen Elementarteilchen sind und man von ihnen keine Beugung am Spalt vermuten würde, wurde diese experimentell nachgewiesen. Dieses Verhalten gibt es sonst nur bei Wellen und ist nicht vereinbar mit der klassischen Vorstellung von Elektronen als Teilchen. In diesem Video erfährst du mehr über die Hintergründe zu diesen Experimenten und lernst wie man die Inteferenzformen berechnen kann.
Transkript Elektronenbeugung am Doppelspalt
Hallo und herzlich willkommen! Ich erkläre hier kurz das Phänomen der Beugung von Elektronenstrahlen beim Durchgang durch eine Doppelspaltblende. Bei diesem Phänomen wird die Wellennatur von Elementarteilchen experimentell bestätigt, so wie sie Louis de Broglie vorausgesagt hat. Du solltest mit der Interferenz von Wellen vertraut sein, du solltest die Plancksche Beziehung W=h×f kennen, die Lichtquantenhypothese verstehen und über de Broglies Hypothese von den Materiewellen informiert sein. Stellen wir uns einen Versuch vor, bei dem wir Kugeln durch einen schmalen Spalt auf einen Wandschirm feuern. Weil die Kugeln mit einer geringen Streuung fliegen, werden einige nicht ganz sauber durch den Spalt gehen, werden die Ränder berühren und etwas abgelenkt werden, sodass auf unserem Schirm nicht alle Kugeln genau in einem Punkt landen, sondern in einem unregelmäßigen Streifen. Aber natürlich wird es im Zentrum eine gewisse Häufung geben. Und wenn wir die Häufigkeit des Auftreffens von Kugeln in einem Querschnitt des Schirms untersuchen, werden wir eine eindeutige Kurve der Häufigkeitsverteilung finden. Wenn wir jetzt unsere Versuchsanordnung erweitern und nun vor den Wandschirm eine Platte mit einem Doppelspalt setzen, um mit einem leichten Hin- und Herschwenken des Gewehrs mal auf den einen, mal auf den anderen Spalt zu schießen, werden wir natürlich 2 solcher Streifen erhalten, und wenn nur die beiden Spalten dicht genug beieinanderliegen, sogar eine einzige große Häufung in der Mitte, wo sich gewissermaßen die Abpraller addieren. Wir können das im Häufigkeitsdiagramm auch sehr gut darstellen, indem wir die beiden Häufigkeitsverteilungen addieren und eine Gesamtverteilung erhalten. Wenn wir dasselbe in sehr viel kleineren Maßstäben mit Elektronen tun, stellen wir fest, dass sich zwar für jeden einzelnen Spalt, gesondert gemessen, genauso eine Häufigkeitsverteilung wie bei Gewehrkugeln ergibt, aber erstaunlicherweise ist die Summe der Treffer aus beiden Spalten gleichzeitig ganz anders verteilt. Wir erhalten nämlich eine Häufigkeitsverteilung, die wie die Intensitätsverteilung eines Interferenzmusters bei Beugung von Wellen am Doppelspalt aussieht. Tatsächlich zeigen Elektronen dieses merkwürdige Verhalten auch, wenn man sie in einem Strahl bündelt und durch einen Kristall sendet. Da sie mit den Atomen des Kristalls wechselwirken, werden wir erwarten, dass sie mit einer gewissen Streuung hinter dem Kristall wieder austreten, also gewissermaßen keinen punktförmigen, sondern einen etwas verschmierten Fleck auf dem Auffangschirm bilden werden. Aber wir sehen etwas ganz Anderes, nämlich einige wenige konzentrische Ringe, die ganz und gar an Welleninterferenz erinnern. Die Ausbildung von Interferenzmustern wirft nun alle Vorstellungen über den Haufen, die wir aus dem Modell der Elektronen als kleine Pakete oder Kügelchen ableiten könnten. Denn wenn wir die summierte Häufigkeitsverteilung hinter dem Doppelspalt mit der Häufigkeitsverteilung hinter einem einzelnen Spalt vergleichen, stellen wir ja fest, dass an manchen Stellen weniger Elektronen ankommen, wenn beide Spalten geöffnet sind. Aber das müsste ja bedeuten, dass die Elektronen durch zum Beispiel den rechten Spalt anders fliegen, wenn der linke Spalt offen ist, als wenn er geschlossen ist. Das kann eigentlich nicht sein. Wir kommen offenbar mit unserer Teilchenvorstellung nicht weiter. Wir können offenkundig nur wie bei der Berechnung von Interferenzfiguren für Wellen verfahren und etwa beim Doppelspaltexperiment die Abstände der entstehenden Streifen mit der Formel berechnen, in der wir bei der Beschreibung des Doppelspaltversuches von Young die Abhängigkeit des Streifenabstandes von der Wellenlänge bestimmt hatten. Damit sind wir dann gewissermaßen bescheiden. Erklären, warum es so ist, wie es ist, können wir nicht. Wir können nur die Phänomene einigermaßen regelmäßig mathematisch beschreiben. Der Versuch, diese Interferenzen darzustellen, ist 1959 von Claus Jönsson in Tübingen gewissermaßen modellhaft vorgenommen worden. Er hat Elektronen in einem elektrischen Feld beschleunigt, wie wir es von der Braunschen Röhre kennen, und mit der Bestimmung des Impulses der beschleunigten Elektronen die Gleichung von de Broglie einsetzen können, um zu berechnen, wie groß die Abstände zwischen den Interferenzstreifen hinter dem Doppelspalt sein müssen. Das Experiment hat ergeben, dass die berechneten Werte richtig waren, das heißt, dass das Modell exakt stimmt. Wenn du magst, kannst du einmal nachrechnen, mit welcher Wellenlänge λ in seinem Versuch Jönsson rechnen musste, wenn du weißt, dass die Beschleunigungsspannung 50kV betrug. Ich will noch einmal kurz zusammenfassen. Beim Beschuss eines Auffangschirms mit einem Elektronenstrahl, der durch eine Doppelspaltblende gelenkt wird, erhalten wir nicht das für kompakte Kügelchen zu erwartende einfache Muster der Überlagerung, sondern eine Interferenzfigur. Damit wird de Broglies Hypothese von der Wellennatur physikalischer Teilchen bestätigt und eindeutig dargestellt. Wir müssen also akzeptieren, dass sich physikalische Objekte in manchem wie kompakte begrenzte Teilchen und gleichzeitig in Anderem wieder wie sich räumlich ausbreitende Wellen verhalten. So viel für diesmal. Viel Vergnügen beim Abenteuer Quantenphysik und vielleicht bis zum nächsten Video!
Elektronenbeugung am Doppelspalt Übung
-
Gib an, wo Kugeln auf einem Auffangbildschirm landen, wenn sie durch einen schmalen Spalt gefeuert werden.
TippsFertige dir eine Skizze an.
Hast du schon einmal etwas von Streuung gehört?
LösungOhne einen schmalen Spalt würden alle Kugeln an einer Stelle registriert werden. Der Spalt (beziehungsweise die Kanten des Spalts) streuen jedoch einzelne Kugeln und lenken diese somit etwas ab.
Somit gibt es eine Häufung in der Mitte des Bildschirmes, doch einige Kugeln landen auch am Rand. Je weiter die Kugeln von der Mitte entfernt landen, desto weniger Kugeln werden an dieser Stelle registriert.
Es ergibt sich eine sehr typische Häufigkeitsverteilung mit einem Maximum in der Mitte der Kurve.
-
Gib an, wie sich Elektronen am Doppelspalt verhalten.
TippsWie verhalten sich Wellen am Doppelspalt?
Was weißt du über Interferenz?
LösungIm Doppelspaltexperiment schickt man Elektronen durch einen Doppelspalt auf einen Auffangbildschirm.
Würden wir wenige Elektronen durch den Doppelspalt schicken, dann könnten wir sie als einzelne Punkte am Schirm erkennen. Offensichtlich ist die Widersprüchlichkeit ihres Verhaltens: Einerseits können Elektronen wie Kanonenkugeln einzeln im Detektor registriert werden, andererseits interferieren sie wie Wasserwellen miteinander.
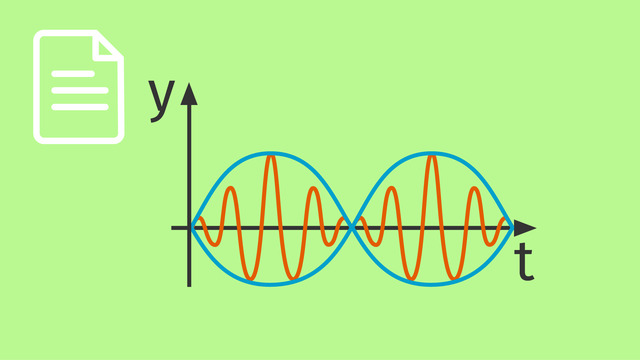
So erhält man eine Häufigkeitsverteilung, die wie die Intensitätsverteilung eines Interferenzmusters bei der Beugung von Wellen am Doppelspalt aussieht.
Wir stellen fest: In Spaltexperimenten mit Elektronen geht bei der Messung etwas vor sich, was die klassische Anschauung nicht erklären kann. Je nach Versuchsbedingungen (enger Spalt oder Doppelspalt) müssen wir entweder vom Wellen- oder Teilchencharakter sprechen.
-
Gib an, wo Elektronen auf einem Auffangbildschirm landen, wenn sie durch einen Kristall gefeuert werden.
TippsWelche besondere Eigenschaft besitzt ein Kristall?
Ein Kristall ist ein Festkörper, dessen Bausteine nicht zufällig, sondern regelmäßig in einer Kristallstruktur angeordnet sind.
LösungEin Kristall ist ein dreidimensionales Objekt, welches eine wesentliche Besonderheit aufweist. Ein Kristall ist nämlich ein Festkörper, dessen Bausteine nicht zufällig, sondern regelmäßig in einer Kristallstruktur angeordnet sind.
Es finden sich auch periodische Abstände zwischen den Atomen wieder, sodass der Interferenzeffekt am Doppelspalt hier im dreidimensionalen Fall beobachtet werden kann. Wie auch am Doppelspalt gibt es Bereiche der Verstärkung und Bereiche der Auslöschung. Somit entstehen konzentrische Kreise, welche einen bestimmten Abstand aufweisen, analog zu den Abständen der Linien auf dem Auffangbildschirm im Doppelspaltexperiment.
-
Gib in der Gleichung zur Berechnung der Linienabstände im Doppelspaltexperiment die physikalischen Größen zu den jeweiligen Formelzeichen an.
TippsDas kleine $d$ gibt in der Regel einen Abstand an.
$\Delta a=\lambda \cdot \frac{d_A}{d_G}$
LösungDie Gleichung zur Berechnung der Linienabstände im Doppelspaltexperiment lautet $\Delta a=\lambda \cdot \frac{d_A}{d_G}$.
Die gesuchte Größe $\Delta a$ ist somit die zu berechnende Linienbreite.
Die Wellenlänge wird in der Physik mit einem Lambda $\lambda$ dargestellt.
Bleiben noch die beiden Abstände $d_A$ und $d_G$, wobei $d_A$ der Abstand zwischen dem Doppelspalt und dem Schirm und $d_G$ der Abstand zwischen den beiden Spalten im Doppelspalt ist.
-
Gib an, welche Aussagen über Elektronen wahr sind.
TippsÜberlege dir, was du über Elektronen (oder andere atomare Partikel) weißt. Kannst du diesen Partikeln einen Teilchen- oder Wellencharakter zuschreiben?
LösungIst das Elektron nun eine Welle oder ein Teilchen?
Das Elektron ist tatsächlich beides gleichzeitig. Je nachdem, welche seiner Eigenschaften man misst, zeigt es sich mehr als Teilchen oder mehr als Welle. Die Beschreibungen bestimmter Phänomene im Wellen- oder im Teilchenbild sind immer nur Vereinfachungen, um es unserer Anschauung leichter zu machen.
Somit ist es wichtig zu wissen, dass beide Betrachtungen (Teilchen und Welle) nur Modelle sind, mit denen man die Natur beschreiben kann. Wie ein Elektron wirklich aussieht, kann bis heute leider kein Mensch wirklich beantworten.
-
Gib den Linienabstand von rotem Licht ($550~nm$), welches durch einen $2~\mu m$ breiten Doppelspalts gefeuert wird, an, wobei der Abstand zwischen dem Doppelspalt und dem Auffangbildschirm $2,6~cm$ beträgt.
TippsSchreibe die gegebenen und gesuchten Größen auf.
Rechne alle Einheiten in Meter um.
LösungUm die Aufgabe lösen zu können, notieren wir zuerst die gegebenen und gesuchten Größen, halten die Formel zur Berechnung fest, setzen die Zahlenwerte ein und halten abschließend das Ergebnis in einem Antwortsatz fest.
Gegeben: $\lambda=550~nm$; $~~~~$ $d_A=2,6~cm$; $~~~~$ $d_G=2~\mu m$
Gesucht: $\Delta a$ in $m$
Formel: $\Delta a= \lambda \cdot \frac{d_A}{d_G}$
Berechnung: $\Delta a= \lambda \cdot \frac{d_A}{d_G}=550~nm\cdot \frac{2,6~cm}{2~\mu m}=550\cdot 10^{-9}~m\cdot \frac{0,026~m}{2\cdot 10^{-6}~m}=0,00715~m=7,15~mm$
Antwortsatz: Der Abstand zwischen den Linien beträgt $7,15~mm$.
9.931
sofaheld-Level
6.600
vorgefertigte
Vokabeln
7.800
Lernvideos
37.167
Übungen
32.630
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Schulstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Physik
- Temperatur
- Schallgeschwindigkeit
- Dichte
- Drehmoment
- Transistor
- Lichtgeschwindigkeit
- Elektrische Schaltungen – Übungen
- Galileo Galilei
- Rollen- Und Flaschenzüge Physik
- Radioaktivität
- Aufgaben zur Durchschnittsgeschwindigkeit
- Lorentzkraft
- Beschleunigung
- Gravitation
- Ebbe und Flut
- Hookesches Gesetz Und Federkraft
- Elektrische Stromstärke
- Elektrischer Strom Wirkung
- Reihenschaltung
- Ohmsches Gesetz
- Freier Fall
- Kernkraftwerk
- Reflexionsgesetz: Ebener Spiegel – Übungen
- Was sind Atome
- Aggregatzustände
- Infrarot, Uv-Strahlung, Infrarot Uv Unterschied
- Isotope, Nuklide, Kernkräfte
- Transformator
- Lichtjahr
- Si-Einheiten
- Fata Morgana
- Gammastrahlung, Alphastrahlung, Betastrahlung
- Kohärenz Physik
- Mechanische Arbeit
- Schall
- Elektrische Leistung
- Dichte Luft
- Ottomotor Aufbau
- Kernfusion
- Trägheitsmoment
- Heliozentrisches Weltbild
- Energieerhaltungssatz Fadenpendel
- Linsen Physik
- Ortsfaktor
- Interferenz
- Diode und Photodiode
- Wärmeströmung (Konvektion)
- Schwarzes Loch
- Frequenz Wellenlänge
- Elektrische Energie




 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?













Liebe Meike,
Sie haben recht - in meiner Rechnung war irgend ein Fehler. Wenn ich es jetzt prüfe, komme ich auf dasselbe Ergebnis wie Sie, pardon !
Das werden wir korrigieren.
Viele Grüße,
kalo
Bei der Berechnung der Wellenlänge komme ich auf ein anderes Ergebnis: Wellenlänge= h / Wurzel(2*e*m_e*5*10^5V) = 1,734 * 10^-12 m. Habe ich irgendwo einen Fehler?