Bestimmtes Integral – Obersumme berechnen
in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Lerntext zum Thema Bestimmtes Integral – Obersumme berechnen
Bestimmtes Integral – benötigtes Vorwissen
Für dieses Thema solltest du wissen, was ein Integral ist. Zur Erinnerung:
Integrale stehen im engen Zusammenhang mit der Differenzialrechnung und können genutzt werden, um Flächeninhalte unter Funktionsgraphen zu berechnen. Formal lässt sich ein bestimmtes Integral so beschreiben:
$\displaystyle\int\limits_{a}^{b} f(x)~\text{d}x$
$a$ und $b$ sind dabei die Integrationsgrenzen, $f(x)$ ist der Integrand mit $x$ als Integrationsvariable und $\text{d}x$ ist das Differenzial.
Mit diesem Integral wird der Flächeninhalt angegeben, der vom Funktionsgraphen von $f(x)$, der $x$-Achse und den beiden Integrationsgrenzen $a$ und $b$ begrenzt wird.
Weiterhin sollte das Prinzip der Annäherung an das Integral über die Ober- und Untersumme, auch bekannt als Streifenmethode des Archimedes, bekannt sein.
Bei der Annäherung an ein Integral über Ober- und Untersumme geht es darum, den Flächeninhalt, den ein bestimmter Funktionsgraph mit der $x$-Achse einschließt, über die Nutzung der Flächeninhalte von Streifen, also von Rechtecken, möglichst genau zu bestimmen. Das Integral wird damit über folgende Formel bestimmt:
$\displaystyle \lim\limits_{n \to \infty} \sum_{i=1}^{n} \dfrac{b~–~a}{n} \cdot f(x_{i})$
Dabei sind $a$ und $b$ die Integrationsgrenzen, $n$ beschreibt die Anzahl der Rechtecke, $\frac{b~–~a}{n}$ gibt die Breite der Rechtecke an und $f(x_{i})$ die Höhe. Je größer $n$ ist, desto genauer wird der Flächeninhalt bestimmt. Deswegen wird normalerweise der Grenzwert von $n$ gegen $\infty$ betrachtet.
Das Summenzeichen beschreibt eine Summe bestimmter Werte, definiert von den Indizes des Summenzeichens.
Das Prinzip der Flächenberechnung mit der Obersumme soll im Folgenden anhand eines Beispiels verdeutlicht werden.
Berechnung eines Flächeninhalts anhand von Ober- und Untersumme
Wir schauen uns die lineare Funktion $f(x) = \frac{1}{2}x + 3$ an. Wir wollen den Flächeninhalt, der in den Grenzen $a = 2$ und $b = 8$ vom Funktionsgraphen und der $x$-Achse eingeschlossen wird, berechnen.
In diesem einfachen Fall lässt sich der Flächeninhalt mit einer Unterteilung in ein rechtwinkliges Dreieck mit der Breite $b~–~a = 8~–~2 = 6$ und der Höhe $f(b)~–~f(a) = f(8)~–~f(2) = 7~–~4 = 3$ sowie ein Rechteck mit den Seitenlängen $6$ und $4$ berechnen.
Damit gilt für den Flächeninhalt:
$A_{Dreieck} + A_{Rechteck} = \dfrac{1}{2} \cdot 6 \cdot 3 + 6 \cdot 4 = 9 + 24 = 33\, [\text{Flächeneinheiten}]$
Wir wollen uns nun die Berechnung des Flächeninhalts mittels Ober- und Untersumme anschauen, um das dahinterliegende Prinzip zu verdeutlichen, das auch auf Funktionsgraphen, die nicht so geradlinig verlaufen, angewendet werden kann.
Berechnung mittels der Obersumme
Bei der Berechnung des Flächeninhalts zwischen Funktionsgraphen und $x$-Achse mittels der Obersumme wird die zu berechnende Fläche in Streifen, also in Rechtecke, aufgeteilt. Die jeweils rechte obere Ecke dieser Rechtecke wird durch den Schnittpunkt mit dem Funktionsgraphen festgelegt. Im Folgenden wurde das Intervall in drei Rechtecke aufgeteilt.
Das Intervall ist $6$ Einheiten breit, also ist bei einer Unterteilung in drei Streifen jeder Streifen genau $2$ Einheiten breit. Die Höhen der Rechtecke können mittels der Funktion bestimmt werden, indem die $x$-Koordinaten der Schnittpunkte $G$, $J$ und $M$ in die Funktionsgleichung eingesetzt werden. Die Höhe des ersten Rechtecks ist beispielsweise $f(a+2) = f(4) = \frac{1}{2} \cdot 4 + 3 = 5$.
So kann nun händisch der Flächeninhalt der Obersumme mit drei Streifen berechnet werden. Die drei Streifen zusammen ergeben einen Flächeninhalt von $36$ FE (Flächeneinheiten). Dir fällt vielleicht auf, dass dies nicht dem Ergebnis entspricht, das wir weiter oben berechnet haben. Das liegt an dem Teil der Rechtecke, die über den Funktionsgraphen hinausragen. Dies sind hier drei Dreiecke mit einer Höhe von $1$ und einer Breite von $2$, was insgesamt einem Flächeninhalt von $3$ Flächeneinheiten entspricht, genau dem Unterschied zwischen dem berechneten Flächeninhalt und dem der Obersumme. Um dem genauen Flächeninhalt näher zu kommen, müssen wir eine Obersumme mit mehr Streifen berechnen.
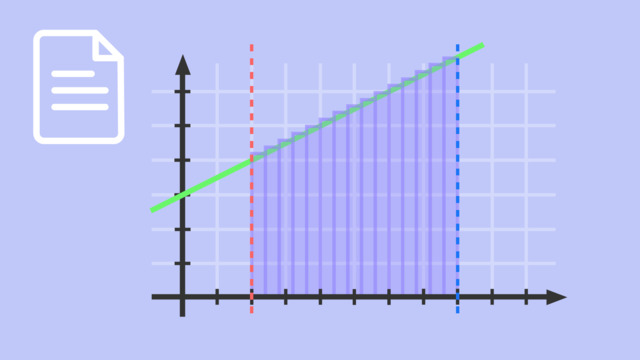
Hier wurde das Intervall in insgesamt fünfzehn Streifen eingeteilt. Der Flächeninhalt setzt sich erneut aus den Flächeninhalten der einzelnen Streifen zusammen, also:
$\displaystyle \sum_{i=1}^{n} \dfrac{b~–~a}{n} \cdot f(x_{i}) = \sum_{i=1}^{15} \dfrac{6}{15} \cdot f(x_{i}) = \dfrac{6}{15} \cdot \sum_{i=1}^{15} f(x_{i})$
Dabei beschreibt $\frac{6}{15}$ die Breite jedes Streifens und $f(x_{i})$ ist der Funktionswert, der die Höhe des jeweiligen Streifens darstellt. Für unsere Funktion sieht die Summe dann wie folgt aus:
$\displaystyle \sum_{i=1}^{15} \dfrac{6}{15} \cdot f(x_{i}) = \dfrac{6}{15} \cdot (4{,}2 + 4{,}4 + 4{,}6 + 4{,}8 + 5 + 5{,}2 + 5{,}4 + 5{,}6 + 5{,}8 + 6 + 6{,}2 + 6{,}4 + 6{,}6 + 6{,}8 + 7) = \dfrac{6}{15} \cdot 84 = 33{,}6\,[\text{FE}]$
Das ist auf jeden Fall dem Flächeninhalt von $33$ FE, den wir im Vorfeld berechnet haben, schon weitaus näher. Doch wie kommen wir nun genau auf den Flächeninhalt von $33$ FE? Dazu müssen wir immer mehr Streifen nehmen, um uns möglichst genau an den Flächeninhalt unter dem Graphen anzunähern. Die Anzahl der Streifen müsste also unendlich groß werden. Bei den Ausdrücken Annäherung und unendlich groß solltest du zuerst an eins denken: an den Grenzwert. Wir nehmen also die oben angegebene Obersummenformel und lassen die Anzahl der Streifen $n$ gegen unendlich laufen.
$\displaystyle \lim\limits_{n \to \infty}\sum_{i=1}^{n} \dfrac{b~–~a}{n} \cdot f(x_{i})$
Allerdings stellt hier das $f(x_{i})$ noch ein Problem dar, da es von der Summe, nicht aber vom Grenzwert abhängt. Aufgrund der Eigenschaft von $x_{i}$, den jeweiligen Streifen nach rechts hin zu begrenzen, und dem Beginn des Intervalls bei $x = 2$ kann man schreiben:
$x_{i} = a + i \cdot \dfrac{b~–~a}{n} = 2 + i \cdot \dfrac{6}{n}$
Eingesetzt in unsere Grenzwertgleichung ergibt das:
$\displaystyle \lim\limits_{n \to \infty}\sum_{i=1}^{n} \dfrac{6}{n} \cdot f\left(2 + i \cdot \dfrac{6}{n}\right)$
Diesen Term können wir in unsere Funktionsgleichung $f(x) = \frac{1}{2} \cdot x + 3$ einsetzen:
$\begin{array}{rrrrl} \displaystyle \lim\limits_{n \to \infty}\sum_{i=1}^{n} \dfrac{6}{n} \cdot f(2 + i \cdot \dfrac{6}{n}) & = & \lim\limits_{n \to \infty} & \displaystyle \sum_{i=1}^{n} & \dfrac{6}{n} \cdot (\dfrac{1}{2} \cdot (2 + i \cdot \dfrac{6}{n}) + 3) \\ & = & \lim\limits_{n \to \infty} & \displaystyle \sum_{i=1}^{n} & \dfrac{6}{n} \cdot (1 + i \cdot \dfrac{6}{2n} + 3) \\ & = & \lim\limits_{n \to \infty} & \displaystyle \sum_{i=1}^{n} & \dfrac{6}{n} \cdot (4 + \dfrac{3}{n} \cdot i) \\ & = & \lim\limits_{n \to \infty} & \displaystyle \sum_{i=1}^{n} & \dfrac{24}{n} + \dfrac{18}{n^2} \cdot i \\ \end{array}$
Nach der Rechenregel für Summenzeichen, nach der man Summen innerhalb von Summenzeichen aufteilen kann, gilt dann:
$\lim\limits_{n \to \infty} \displaystyle \sum_{i=1}^{n} \dfrac{24}{n} + \dfrac{18}{n^2} \cdot i = \lim\limits_{n \to \infty} \displaystyle \left(\sum_{i=1}^{n} \dfrac{24}{n} + \sum_{i=1}^{n} \dfrac{18}{n^2} \cdot i\right)$
Nun kommen noch die folgenden Summenregeln zum Einsatz:
$\displaystyle \sum_{k=1}^{n} a = a \cdot n$
$\displaystyle \sum_{k=1}^{n} c \cdot a_{k} = c \cdot \displaystyle \sum_{k=1}^{n} a_{k}$
Mit diesen können wir die beiden Summenzeichen in unserer Gleichung vereinfachen.
$\lim\limits_{n \to \infty} \displaystyle \left(\sum_{i=1}^{n} \dfrac{24}{n} + \sum_{i=1}^{n} \dfrac{18}{n^{2}} \cdot i\right)$
$= \lim\limits_{n \to \infty} \left(\dfrac{24}{n} \cdot n+ \dfrac{18}{n^{2}} \cdot \displaystyle \sum_{i=1}^{n} i\right)$
$= \lim\limits_{n \to \infty} \displaystyle \left(24 + \dfrac{18}{n^{2}} \cdot \sum_{i=1}^{n} i\right)$
Die Summe am Ende kann man noch mit der gaußschen Summenformel umschreiben.
$\begin{array}{rrrrl} \displaystyle \lim\limits_{n \to \infty} (24 + \dfrac{18}{n^2} \cdot \sum_{i=1}^{n} i) & = & \displaystyle \lim\limits_{n \to \infty} & (24 & + \dfrac{18}{n^2} \cdot \dfrac{n \cdot (n + 1)}{2}) \\ & = & \displaystyle \lim\limits_{n \to \infty} & (24 & + \dfrac{18 \cdot n \cdot (n + 1)}{2n^2}) \\ \end{array}$
Im Bruch können nun die $18$ mit der $2$ und die $n$ miteinander gekürzt werden.
$\begin{array}{rrrrl} \displaystyle \lim\limits_{n \to \infty}(24 + \dfrac{18 \cdot n \cdot (n + 1)}{2n^2}) & = & \displaystyle \lim\limits_{n \to \infty} & (24 & + \dfrac{9 \cdot (n + 1)}{n}) \\ \\ & = & \displaystyle \lim\limits_{n \to \infty} & (24 & + \dfrac{9n + 9}{n}) \\ \\ & = & \displaystyle \lim\limits_{n \to \infty} & (24 & + \dfrac{9n}{n} + \dfrac{9}{n}) \\ \\ & = & \displaystyle \lim\limits_{n \to \infty} & (24 & + 9 + \dfrac{9}{n}) \\ \\ & = & \displaystyle \lim\limits_{n \to \infty} & (33 & + \dfrac{9}{n}) \\ \\ & = & 33 & & \\ \end{array}$
Und damit erhalten wir den gleichen Flächeninhalt, den wir zu Anfang berechnet haben, den genauen Flächeninhalt.
Berechnung mittels Untersumme
Genauso wie bei der Obersumme funktioniert es auch mit der Untersumme. Hier befinden sich die Rechtecke lediglich unter dem Funktionsgraphen und nicht darüber.
Der Unterschied ist hier, dass sich der Flächeninhalt der Untersumme von unten an den genauen Flächeninhalt annähert. Deswegen ist der Flächeninhalt der drei Streifen nicht um $3$ größer als der genaue Flächeninhalt, sondern um $3$ kleiner, er ist hier nämlich $30$ Flächeneinheiten groß. Dieser Unterschied in der Grenzwertberechnung zeigt sich darin, dass die $x_i$ anders definiert sind. Bei der Obersumme gilt:
$x_i = a + i \cdot \dfrac{b~–~a}{n}$
Bei der Untersumme gilt dagegen:
$x_i = a + (i~–~1) \cdot \dfrac{b~–~a}{n}$
Also ändert sich die Grenzwertgleichung wie folgt:
$\displaystyle \lim\limits_{n \to \infty}\sum_{i=1}^{n} \dfrac{b~–~a}{n} \cdot f(x_{i}) = \displaystyle \lim\limits_{n \to \infty}\sum_{i=1}^{n} \dfrac{6}{n} \cdot f(2 + (i~–~1) \cdot \dfrac{6}{n})$
Nach Berechnung des Grenzwerts kommt dann aber ebenfalls ein Flächeninhalt von $33$ Flächeneinheiten heraus.
Bestimmtes Integral – Zusammenfassung
Die Berechnung eines bestimmten Integrals mithilfe von Ober- und Untersumme ist die Annäherung an den Flächeninhalt unter dem Graphen in einem bestimmten Intervall. Dabei berechnet sich das Integral wie folgt:
Obersumme:
$\displaystyle O(n) = \sum_{i=1}^{n} \dfrac{b~–~a}{n} \cdot f(a + i \cdot \dfrac{b~–~a}{n})$
Untersumme:
$\displaystyle U(n) = \sum_{i=1}^{n} \dfrac{b~–~a}{n} \cdot f(a + (i~–~1) \cdot \dfrac{b~–~a}{n})$
Bestimmtes Integral:
$\displaystyle \lim\limits_{n \to \infty} O(n)= \lim\limits_{n \to \infty} U(n)= \int\limits_{a}^{b} f(x)~\text{d}x$
Häufig gestellte Fragen zum Thema Bestimmtes Integral
9.038
sofaheld-Level
6.601
vorgefertigte
Vokabeln
7.581
Lernvideos
35.734
Übungen
32.493
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Schulstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebeziehungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Satz Des Pythagoras
- Dreieck Grundschule
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Winkelsummen in Dreiecken und Vierecken – Übungen
- Zahlen In Worten Schreiben
- Meter
- Orthogonalität
- Schriftlich Multiplizieren
- Brüche gleichnamig machen
- Brüche Multiplizieren
- Brüche multiplizieren – Übungen
- Potenzgesetze


 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?