Komplexe Zahlen

Inhaltsverzeichnis zum Thema

• Was sind komplexe Zahlen?
• Darstellung von komplexen Zahlen
• Die algebraische Darstellung
• Die Darstellung in der Gauß’schen Zahlenebene
• Die Darstellung mit Polarkoodinaten sowie in Exponentialform
• Wie kannst du mit komplexen Zahlen rechnen?
• Die Addition oder Subtraktion von komplexen Zahlen
• Die Multiplikation von komplexen Zahlen
• Die Division von komplexen Zahlen
• Der Betrag einer komplexen Zahl

Was sind komplexe Zahlen?

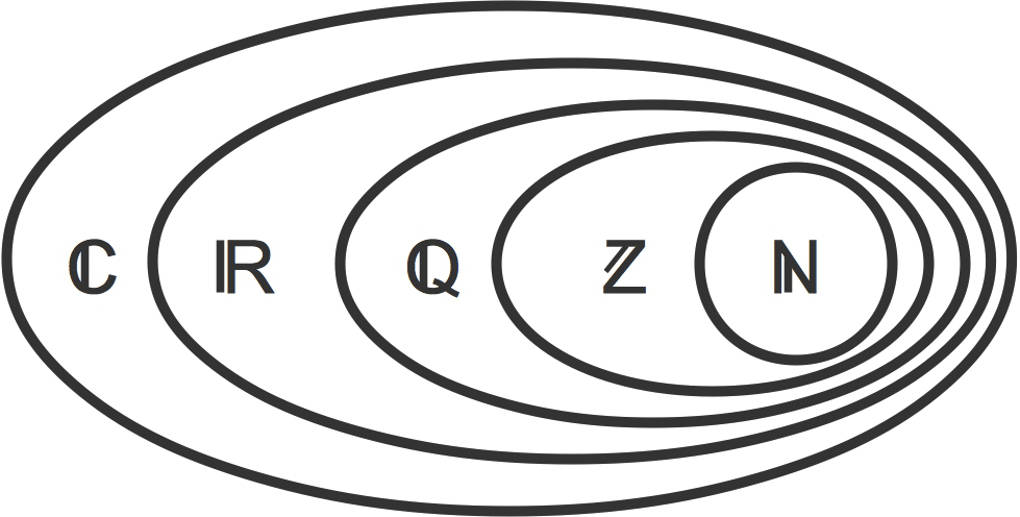
Hier siehst du eine Übersicht der Zahlenbereiche. Jedes Mal, wenn eine Gleichung in einem gegebenen Zahlenbereich nicht lösbar ist, wird dieser erweitert, so dass die Gleichung lösbar ist.

So ist zum Beispiel die Gleichung $x^2=2$ im Bereich der rationalen Zahlen $\mathbb{Q}$ nicht lösbar. Die rationalen Zahlen werden ergänzt um die irrationalen Zahlen zu den reellen Zahlen $\mathbb{R}$.

Allerdings ist auch im Bereich der reellen Zahlen nicht jede Gleichung lösbar, z.B. besitzt

$x^2=-1$.

keine reelle Lösung. Wie du sicherlich gelernt hast, gilt: Man kann nicht die Wurzel aus einer negativen Zahl ziehen.

Doch! Die komplexen Zahlen sind über die imaginäre Zahl $i$ definiert. Es gilt

$i^2=-1$,

also

$i=\sqrt{-1}$.

Darstellung von komplexen Zahlen

Die algebraische Darstellung

Die normale oder algebraische Darstellung, auch kartesische Darstellung genannt, einer komplexen Zahl lautet

$z=a+b\cdot i$.

Dabei wird $a$ als der Realteil Re$(z)$ und $b$ als der Imaginärteil Im$(z)$ bezeichnet.

Das konjugiert Komplexe einer komplexen Zahl ist gegeben durch

$\bar z=a-b\cdot i$.

Das bedeutet, dass bei dem Imaginärteil das Vorzeichen vertauscht wird.

Beispiele:

• $z_1=1+4i$ Hier ist der Realteil $a=1$ und der Imaginärteil $b=4$.
• $\overline{z_1}=1-4i$ Der Realteil ist immer noch $a=1$, allerdings ist der Imaginärteil $b=-4$.
• $z_2=5+2i$ mit dem Realteil $a=5$ und dem Imaginärteil $b=2$.

Die Darstellung in der Gauß’schen Zahlenebene

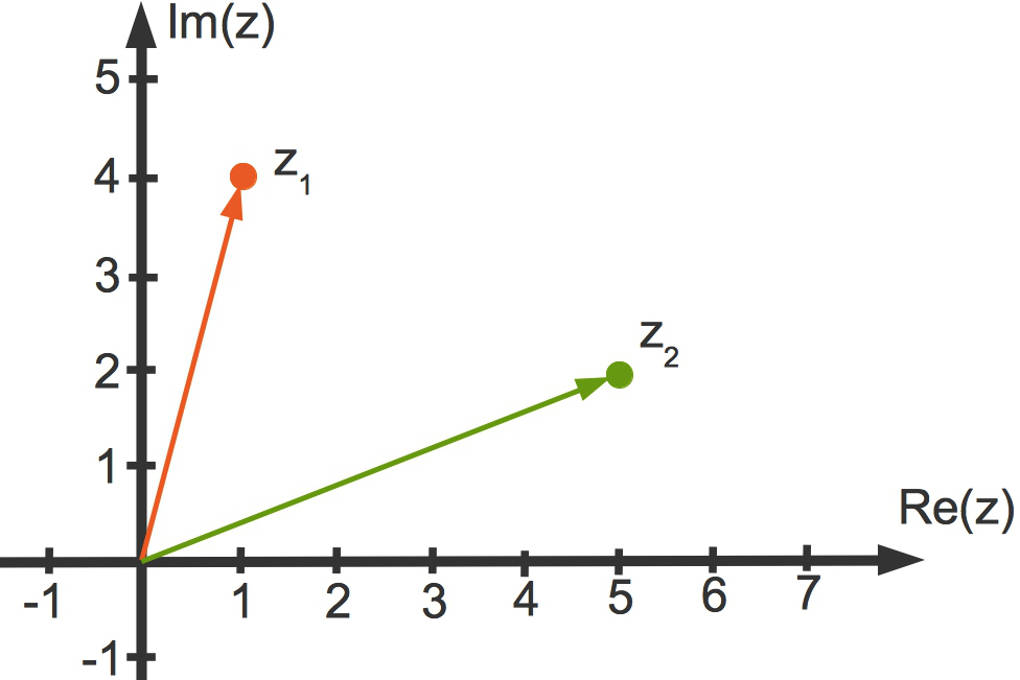
Komplexe Zahlen können in der Gauß’schen Zahlenebene dargestellt werden. Du kannst dir dies wie Vektoren im $\mathbb{R}^2$ vorstellen. Auf der x-Achse wird der Realteil und auf der y-Achse der Imaginärteil der komplexen Zahl angegeben. Das bedeutet, dass eine komplexe Zahl einem Punkt der Gauß’schen Zahlenebene, respektive dem zu diesem Punkt gehörenden Ortsvektor, entspricht.

Dies kannst du für die beiden obigen komplexen Zahlen $z_1=1+4i$ sowie $z_2=5+2i$ hier sehen:

Die Darstellung mit Polarkoodinaten sowie in Exponentialform

Komplexe Zahlen können auch mit Hilfe von Polarkoordinaten oder in Exponentialform dargestellt werden. Schaue dir das Beispiel der komplexen Zahl $z=a+b\cdot i$ an.

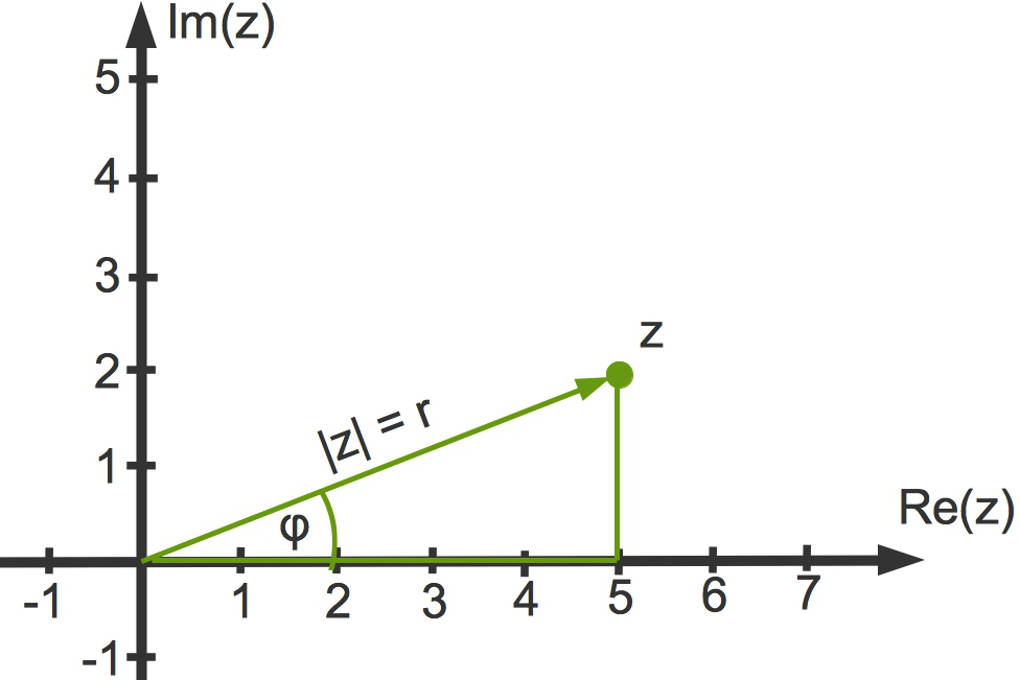
Zu jeder komplexen Zahl $z=a+b\cdot i$ gehört ein Winkel $\varphi$, welchen der Vektor $z$ mit der x-Achse einschließt.

Wie du in dem Bild sehen kannst, erhältst du ein rechtwinkliges Dreieck mit den Kathetenlängen $a$ und $b$ sowie der Hypotenuse $r=|z|$, dem Betrag der komplexen Zahl $z$.

Damit ist

• $\cos(\varphi)=\frac ar$ oder, äquivalent dazu, $a=r\cdot \cos(\varphi)$. Dies ist der Realteil der komplexen Zahl.
• $\sin(\varphi)=\frac br$ oder, äquivalent dazu, $b=r\cdot \sin(\varphi)$. Dies ist der Imaginärteil der komplexen Zahl.

Nun kannst du die komplexe Zahl $z$ schreiben als

$\begin{array}{rcl} z&=&r\cdot\cos(\varphi)+r\cdot \sin(\varphi)\cdot i\\ &=&r\cdot(\cos(\varphi)+\sin(\varphi)\cdot i) \end{array}$

Dies ist die sogenannte Polarform.

Mit $r=|z|$ sowie dem Winkel $\varphi$ kann eine komplexe Zahl auch in Exponentialform geschrieben werden:

$z=r\cdot e^{i\cdot\varphi}$.

Dabei ist $e\approx2,71828$ die Euler’sche Zahl.

Wie kannst du mit komplexen Zahlen rechnen?

Seien $z_1=a+b\cdot i$ sowie $z_2=c+d\cdot i$ zwei komplexe Zahlen.

Die Addition oder Subtraktion von komplexen Zahlen

Für die Addition oder Subtraktion zweier komplexer Zahlen gilt

$\begin{array}{rcl}z_1\pm z_2&=&(a+b\cdot i)\pm (c+d\cdot i)\\ &=&(a\pm c)+(b\pm d)\cdot i \end{array}$

Das bedeutet, dass der Realteil und auch der Imaginärteil der Summe (Differenz) zweier komplexer Zahlen die Summe (Differenz) der einzelnen Realteile beziehungsweise der Imaginärteile ist.

Beispiele

• $(1+4i)+(5+2i)=6+6i$
• $(1+4i)-(5+2i)=-4+2i$

Die Multiplikation von komplexen Zahlen

Bei der Multiplikation zweier komplexer Zahlen gehst du vor wie beim Multiplizieren zweier Binome.

$\begin{array}{rcl}z_1\cdot z_2&=&(a+b\cdot i)\cdot (c+d\cdot i)\\ &=&a\cdot c+a\cdot d\cdot i +b\cdot c\cdot i+b\cdot d\cdot i^2\\ &=&a\cdot c+a\cdot d\cdot i +b\cdot c\cdot i-b\cdot d\\ &=&a\cdot c-b\cdot d+(a\cdot d+b\cdot c)\cdot i \end{array}$

Du siehst in der zweiten Zeile, dass $b\cdot d\cdot i^2=-b\cdot d\cdot$ ist. Dies liegt gerade an der Definition der imaginären Zahl $i$, für die $i^2=-1$ gilt.

Beispiel

$(1+4i)\cdot(5+2i)=5-8+(2+20)\cdot i=-3+22i$

Die Division von komplexen Zahlen

Zur Division zweier komplexer Zahlen wendest du einen Trick an. Erweitere den Quotienten mit dem konjugiert Komplexen des Nenners:

$\begin{array}{rcl}\frac{z_1}{z_2}&=&\frac{a+b\cdot i}{c+d\cdot i}\\ &=&\frac{a+b\cdot i}{c+d\cdot i}\cdot \frac{c-d\cdot i}{c-d\cdot i}\\ &=&\frac{(a+b\cdot i)\cdot(c-d\cdot i)}{(c+d\cdot i)\cdot(c-d\cdot i)}\\ &=&\frac{ac+bd+(bc-ad)\cdot i}{c^2+d^2}\\ &=&\frac{ac+bd}{c^2+d^2}+\frac{bc-ad}{c^2+d^2}\cdot i \end{array}$

Beispiel

$\begin{array}{rcl}\frac{1+4\cdot i}{5+2\cdot i}&=&\frac{5+8}{5^2+2^2}+\frac{20-2}{5^2+2^2}\cdot i\\ &=&\frac{13}{\sqrt{29}}+\frac{18}{\sqrt{29}}\cdot i \end{array}$

Der Betrag einer komplexen Zahl

Der Betrag einer komplexen Zahl entspricht der Länge des Vektors im Gauß’schen Koordinatensystem. Es ist

$\begin{array}{rcl}|z|&=&\sqrt{z\cdot \bar z}\\ &=&\sqrt{(a+b\cdot i)\cdot(a-b\cdot i)}\\ &=&\sqrt{a^2-a\cdot b\cdot i+a\cdot b\cdot i-b^2\cdot i^2}\\ &=&\sqrt{a^2+b^2}. \end{array}$

Beispiele

• $|1+4\cdot i|=\sqrt{1^2+4^2}=\sqrt{17}$
• $|5+2\cdot i|=\sqrt{5^2+2^2}=\sqrt{29}$

Abschließend siehst du, wie du zwei komplexe Zahlen in der Exponentialform multiplizieren kannst, am Beispiel $z_1=1+4i$ und $z_2=5+2i$.

• Bestimme den Winkel $\varphi$ zu jeder der beiden komplexen Zahlen:

$\quad~~~\varphi_1=\tan^{-1}\left(\frac41\right)\approx 76^\circ$ und

$\quad~~~\varphi_2=\tan^{-1}\left(\frac25\right)\approx 21,8^\circ$.

• Damit ist

$\quad~~~z_1=\sqrt{17}\cdot e^{76i}$ sowie

$\quad~~~z_2=\sqrt{29}\cdot e^{21,8i}$.

• Nun können die beiden Zahlen multipliziert werden:

$\quad~~~\begin{array}{rcl}z_1\cdot z_2&=&\sqrt{17}\cdot e^{76i}\cdot \sqrt{29}\cdot e^{21,8i}\\ &=&\sqrt{493}\cdot e^{97,8i}\end{array}$