Beweismethoden
Indutionsanfang, Induktionsbehauptung, Induktionsbeweis, Induktionsschluss, natürliche Zahlen
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
Einführung und Überblick
Stell dir vor, du entdeckst einen mathematischen Zusammenhang. Zum Beispiel glaubst du, dass die Summe zweier ungerader Zahlen immer gerade sein muss. Es genügt nun nicht, sehr viele Beispiele dafür zu finden. Du musst diesen Zusammenhang beweisen, damit klar ist, dass er auch wirklich gilt.
Nehmen wir einmal an, dass du beweisen möchtest, dass aus der Aussage $A$ auch die Aussage $B$ folgt. Man schreibt dies mathematisch so: $A~\Rightarrow ~B$. Du kannst dann auf verschiedene Arten vorgehen:
- Direkter Beweis: Du beginnst mit der Aussage $A$ und gelangst über logisch korrekte Schlüsse zu der Aussage $B$.
- Widerspruchsbeweis (zB. Die Unendlichkeit der Primzahlen: Du nimmst an, dass die Aussage $B$, welche du zeigen möchtest, nicht gilt. Du gehst also von der Negation $\neg B$ aus. Schließlich gelangst du über logisch korrekte Schlüsse zu einem Widerspruch.
- Induktionsbeweis: Einen solchen Beweis verwendest du, wenn du die Gültigkeit von Aussagen $A_{n}$ für $n\in\mathbb{N}$ nachweisen willst.
- Bei manchen Aussagen kannst du auch einen geometrischen Beweis verwenden.
Im Folgenden wirst du zu jeder der Beweismethoden ein Beispiel sehen.
Direkter Beweis
Aussage: Die Summe zweier ungerader Zahlen $p$ und $q$ ist immer gerade.
- Wenn $p$ und $q$ jeweils ungerade sind, lassen sie sich mit $p=2n+1$ und $q=2m+1$ darstellen, wobei sowohl $n$ als auch $m$ eine natürliche Zahl ist.
- Damit ist $p+q=2n+1+2m+1=2n+2m+2=2(n+m+1)$.
- Egal, welche Zahl in der Klammer steht, das Doppelte dieser Zahl ist immer durch zwei teilbar und somit gerade.
Damit ist die Aussage bewiesen.
Widerspruchsbeweis
Aussage: Die Wurzel von $2$ ist eine irrationale Zahl.
Wir nehmen an, dass diese Aussage nicht gilt. Dann ist $\sqrt 2$ eine rationale Zahl und lässt sich also so schreiben $\sqrt 2=\frac pq$. Dabei sind $p$ und $q$ nicht gleichzeitig gerade Zahlen. Warum ist das so? Wenn sowohl der Zähler als auch der Nenner gerade ist, kannst du so lange mit $2$ kürzen, bis mindestens eine der beiden Zahlen ungerade ist. Der folgende Beweis funktioniert für jeden der Fälle:
- Der Zähler ist gerade und der Nenner ungerade.
- Der Zähler ist ungerade und der Nenner gerade.
- Sowohl Zähler als auch Nenner sind ungerade.
Du siehst nun den Beweis für den Fall, dass der Zähler gerade und der Nenner ungerade ist. Dann gilt $p=2n$ und $q=2m+1$. Dabei sind $n$ und $m$ natürliche Zahlen. Nun folgt für $\sqrt{2}=\frac{p}{q}$ folgende Rechnung:
$\begin{array}{rclll} \sqrt{2}&=&\frac{(2n)}{(2m+1)}&|&\text{quadrieren}\\ 2&=&\frac{(2n)^2}{(2m+1)^2}&|&\cdot (2m+1)^2\\ 2\cdot (2m+1)^2&=&(2n)^2&|&1.\text{ binomische Formel}\\ 2\cdot (4m^2+4m+1)&=&4n^2&|&:2\\ 4m^2+4m+1&=&2n^2 \end{array}$
Schau dir die letzte Zeile genau an:
- Auf der linken Seite steht eine ungerade Zahl.
- Auf der rechten Seite steht eine gerade Zahl.
- Das bedeutet, dass es eine Zahl geben muss, die sowohl gerade als auch ungerade ist. Dies ist jedoch unmöglich.
Die obige Annahme führt zu einem Widerspruch und kann somit nicht korrekt sein. Was wiederum bedeutet, dass $\sqrt 2$ tatsächlich irrational ist.
Vollständige Induktion
Es gibt eine Geschichte von dem neunjährigen Carl Friedrich Gauß: Er sollte die ersten $100$ Zahlen addieren. Kaum war die Aufgabe gestellt, hatte der kleine Gauß sie auch schon gelöst. Das Ergebnis ist $5050$. Nur, wie kam er darauf?
Aussage: Es gilt die Gauß'sche Summenformel: $\sum\limits_{i=1}^{n}i=\frac{n\cdot (n+1)}2$
Diese Formel hat der kleine Gauß verwendet: $\sum\limits_{i=1}^{100}i=\frac{100\cdot (100+1)}2=5050$.
Diese Aussage soll nun mit Hilfe der vollständigen Induktion bewiesen werden. Das Vorgehen sieht dabei immer so aus:
Induktionsanfang: Die Aussage wird für $n=1$ bewiesen.
Es muss also $\sum\limits_{i=1}^{1}i=\frac{1\cdot (1+1)}2$ sein. Das prüfen wir einmal.
- Auf der linken Seite steht nur ein Summand, die $1$.
- Auf der rechten Seite steht $\frac{1\cdot (1+1)}2=\frac22=1$.
Die Aussage stimmt also für $n=1$.
Induktionsannahme: Du nimmst an, dass die Aussage für $n$ gilt, also $\sum\limits_{i=1}^{n}i=\frac{n\cdot (n+1)}2$.
Induktionsschluss: Du weist nach, dass die Aussage auch für den Nachfolger von $n$, also für $n+1$ gefolgert werden kann. Dabei verwendest du die Induktionsannahme.
- Schreib zunächst die Aussage für $n+1$ auf: $\sum\limits_{i=1}^{n+1}i=\frac{(n+1)\cdot (n+1+1)}2=\frac{(n+1)\cdot(n+2)}{2}$. Du ersetzt also überall $n$ durch $n+1$.
- Beginne mit der linken Seite:
$\begin{array}{rclll} \sum\limits_{i=1}^{n+1}i&=&\sum\limits_{i=1}^{n}i+(n+1)&|&\text{Abspalten des letzten Summanden}\\ &=&\frac{n\cdot (n+1)}{2}+(n+1)&|&\text{Induktionsannahme}\\ &=&\frac{n\cdot (n+1)}{2}+\frac{2(n+1)}{2}\\ &=&\frac{n\cdot (n+1)+2(n+1)}{2}\\ &=&\frac{(n+2)\cdot (n+1)}{2}\\ &=&\frac{(n+1)\cdot(n+2)}{2} \end{array}$
Ganz am Schluss steht dort tatsächlich die rechte Seite aus dem Induktionsschluss. Damit ist die Aussage bewiesen.
Warum ist damit eigentlich die Aussage bewiesen? Bei einem Induktionsbeweis beginnst du immer mit der kleinsten betrachteten natürlichen Zahl, in dem obigen Beispiel mit der $1$. Wenn du nun für jede Zahl beweisen kannst, dass die Aussage auch für deren Nachfolger gilt, folgt mit der Richtigkeit der Aussage für $n=1$ auch die Richtigkeit für deren Nachfolger, also $n=2$. Damit folgt die Richtigkeit auch für den Nachfolger von $2$, also für $n=3$ und so weiter.
Geometrischer Beweis
Abschließend siehst du noch einen geometrischen Beweis für die 1. binomische Formel:
Aussage: Es gilt die 1. binomische Formel: $(a+b)^{2}=a^{2}+2ab+b^{2}$.
Wir starten mit einem Quadrat mit der Seitenlänge $a+b$ und damit dem Flächeninhalt $(a+b)^{2}$. Dies ist die linke Seite der binomischen Formel.
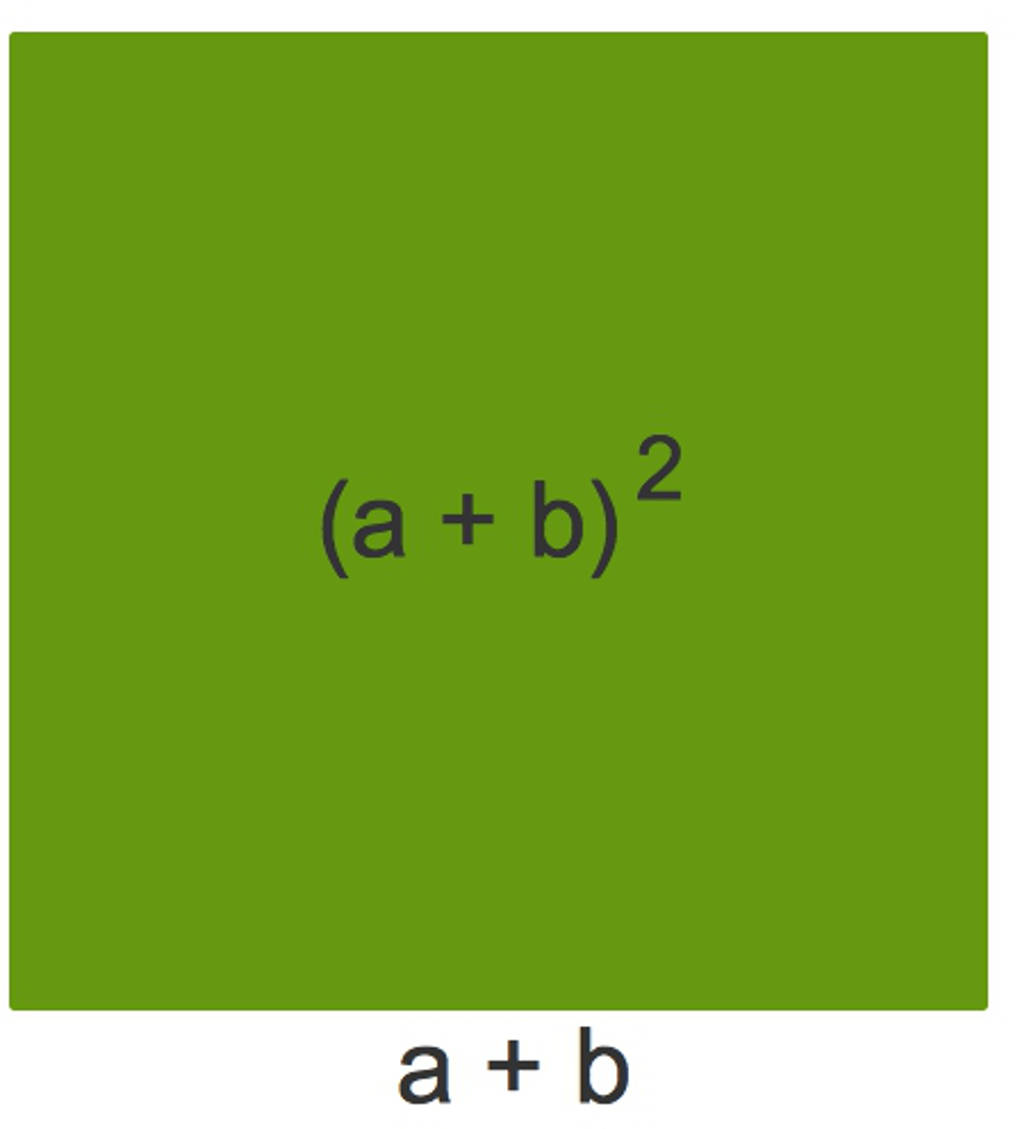
Teile nun dieses Quadrat wie im folgenden Bild auf:
- Oben links siehst du ein rotes Quadrat mit der Seitenlänge $a$ und dem Flächeninhalt $a^{2}$.
- Unten rechts ist ein blaues Quadrat mit der Seitenlänge $b$ und dem Flächeninhalt $b^{2}$.
- Die beiden verbleibenden Rechtecke haben jeweils den Flächeninhalt $ab$.

Schließlich kannst du das grüne Quadrat aufschneiden in Teilflächen. Dabei ändert sich der gesamte Flächeninhalt nicht.
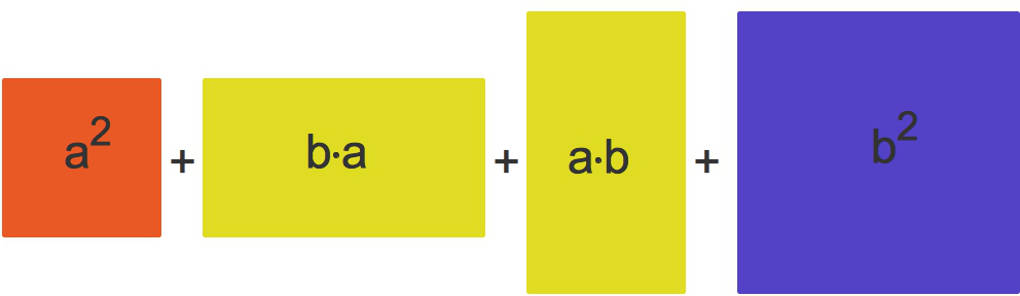
Gesamt gilt dann $(a+b)^{2}=a^{2}+2ab+b^{2}$. Damit ist die 1. binomische Formel bewiesen.
Alle Videos zum Thema
Videos zum Thema
Beweismethoden (4 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Beweismethoden (4 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Primzahlen
- Geometrische Lagebeziehungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Quadrat
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Was Ist Eine Viertelstunde
- Prisma
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Aufbau von Dreiecken
- Quader
- Satz Des Pythagoras
- Dreieck Grundschule
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Volumen Kugel
- Zahlen In Worten Schreiben
- Meter
- Orthogonalität
- Schriftlich Multiplizieren
- Brüche gleichnamig machen
- Brüche Multiplizieren
- Potenzgesetze
- Distributivgesetz
- Flächeninhalt Dreieck
- Rationale Zahlen
- Volumen Berechnen
- Brüche Addieren
- Kongruenz
- Exponentialfunktion
- Exponentialfunktion Beispiel









 Geometrische Beweise – Erklärung am Satz des Thales
Geometrische Beweise – Erklärung am Satz des Thales
 Vollständige Induktion – Erklärung an der Gauß'schen Summenformel
Vollständige Induktion – Erklärung an der Gauß'schen Summenformel
 Direkter Beweis – Erklärung und Beispiel
Direkter Beweis – Erklärung und Beispiel
 Widerspruchsbeweise – Unendlichkeit der Primzahlen
Widerspruchsbeweise – Unendlichkeit der Primzahlen









